
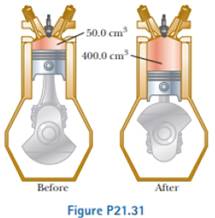
During the power stroke in a four-stroke automobile engine, the piston is forced down as the mixture of combustion products and air undergoes an adiabatic expansion. Assume (1) the engine is running at 2 500 cycles/min; (2) the gauge pressure immediately before the expansion is 20.0 atm; (3) the volumes of the mixture immediately before and after the expansion are 50.0 cm3 and 400 cm3, respectively (Fig. P21.31); (4) the time interval for the expansion is one-fourth that of the total cycle; and (5) the mixture behaves like an ideal gas with specific heat ratio 1.40. Find the average power generated during the power stroke.
Trending nowThis is a popular solution!

Chapter 21 Solutions
Physics for Scientists and Engineers, Technology Update (No access codes included)
- Figure P21.45 shows a cyclic process ABCDA for 1.00 mol of an ideal gas. The gas is initially at Pi = 1.50 105 Pa, Vi = 1.00 103 m3 (point A in Fig. P21.45). a. What is the net work done on the gas during the cycle? b. What is the net amount of energy added by heat to this gas during the cycle? FIGURE P21.45arrow_forwardThe compression ratio of an Otto cycle as shown in Figure 21.12 is VA/VB = 8.00. At the beginning A of the compression process, 500 cm3 of gas is at 100 kPa and 20.0C. At the beginning of the adiabatic expansion, the temperature is TC = 750C. Model the working fluid as an ideal gas with = 1.40. (a) Fill in this table to follow the states of the gas: (b) Fill in this table to follow the processes: (c) Identify the energy input |Qh|, (d) the energy exhaust |Qc|, and (e) the net output work Weng. (f) Calculate the efficiency. (g) Find the number of crankshaft revolutions per minute required for a one-cylinder engine to have an output power of 1.00 kW = 1.34 hp. Note: The thermodynamic cycle involves four piston strokes.arrow_forwardA 1.00-mol sample of an ideal monatomic gas is taken through the cycle shown in Figure P18.63. The process AB is a reversible isothermal expansion. Calculate (a) the net work done by the gas, (b) the energy added to the gas by heat, (c) the energy exhausted from the gas by heat, and (d) the efficiency of the cycle. (e) Explain how the efficiency compares with that of a Carnot engine operating between the same temperature extremes. Figure P18.63arrow_forward
- You have a particular interest in automobile engines, so you have secured a co-op position at an automobile company while you attend school. Your supervisor is helping you to learn about the operation of an internal combustion engine. She gives you the following assignment, related to a simulation of a new engine she is designing. A gas, beginning at PA = 1.00 atm, VA = 0.500 L, and TA = 27.0C, is compressed from point A on the PV diagram in Figure P19.31 (page 530) to point B. This represents the compression stroke in a fourcycle gasoline engine. At that point, 132 J of energy is delivered to the gas at constant volume, taking the gas to point C. This represents the transformation of potential energy in the gasoline to internal energy when the spark plug fires. Your supervisor tells you that the internal energy of a gas is proportional to temperature (as we shall find in Chapter 20), the internal energy of the gas at point A is 200 J, and she wants to know what the temperature of the gas is at point C. Figure P19.31arrow_forwardThe energy input to an engine is 3.00 times greater than the work it performs. (i) What is its thermal efficiency? (a) 3.00 (b) 1.00 (c) 0.333 (d) impossible to determine (ii) What fraction of the energy input is expelled to the cold reservoir? (a) 0.333 (b) 0.667 (c) 1.00 (d) impossible to determinearrow_forward
 Principles of Physics: A Calculus-Based TextPhysicsISBN:9781133104261Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning
Principles of Physics: A Calculus-Based TextPhysicsISBN:9781133104261Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning Physics for Scientists and Engineers, Technology ...PhysicsISBN:9781305116399Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning
Physics for Scientists and Engineers, Technology ...PhysicsISBN:9781305116399Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning Physics for Scientists and Engineers with Modern ...PhysicsISBN:9781337553292Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning
Physics for Scientists and Engineers with Modern ...PhysicsISBN:9781337553292Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning Physics for Scientists and EngineersPhysicsISBN:9781337553278Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning
Physics for Scientists and EngineersPhysicsISBN:9781337553278Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning Physics for Scientists and Engineers: Foundations...PhysicsISBN:9781133939146Author:Katz, Debora M.Publisher:Cengage Learning
Physics for Scientists and Engineers: Foundations...PhysicsISBN:9781133939146Author:Katz, Debora M.Publisher:Cengage Learning




