Elementary Geometry for College Students
Elementary Geometry for College Students
6th Edition
ISBN: 9781285195698
Author: Daniel C. Alexander, Geralyn M. Koeberlein
Publisher: Cengage Learning
bartleby

Concept explainers

Sequence and Series
A sequence is defined as a collection of things. Series is defined to sum the things one by one in the sequence. It was invented by German mathematician Carl Friedrich Gauss.
bartleby

Videos

Textbook Question
Book Icon
Chapter 2.4, Problem 30E
Given: Equiangular Δ R S T

Prove:		 R V → bisects ∠ S R T
Δ R V S is a right Δ

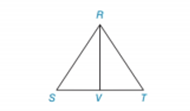Chapter 2.4, Problem 30E, Given: Equiangular RST Prove: RV bisects SRT RVS is a right
Expert Solution & Answer
Check Mark
bartleby

Trending nowThis is a popular solution!

See solution
Check out sample textbook solution
Blurred answer
Previous
Chapter 2.4, Problem 29E
Next
Chapter 2.4, Problem 31E
Students have asked these similar questions
PN bisects MQ ZM and 2Q are right angles ΔΡOR ΔΝMR Given: Prove: R
let fo) - Bx"t2e?kacty fnd Hhe Prst three denivahes
C.7-V's with joint Exomple C How): het X oned Y are e-w P. G Findd the Value ofC Fined PCicXくて→2くりくる) 3 Finel P(X+サくる)

Chapter 2 Solutions

Elementary Geometry for College Students

Ch. 2.1 - Prob. 1ECh. 2.1 - For Exercises 1 to 4, lm with transversal v. If...Ch. 2.1 - For Exercises 1 to 4, lm with transversal v. If...Ch. 2.1 - Prob. 4ECh. 2.1 - Use drawings, as needed, to answer each question....Ch. 2.1 - Use drawings, as needed, to answer each question....Ch. 2.1 - Use drawings, as needed, to answer each question....Ch. 2.1 - Use drawings, as needed, to answer each question....Ch. 2.1 - Use drawings, as needed, to answer each question....Ch. 2.1 - In Euclidean geometry, how many lines can be drawn...
Ch. 2.1 - Lines r and s are cut by the transversal t. Which...Ch. 2.1 - ADBC, ABDC, and mA=92. Find: a mB b mC c mDCh. 2.1 - lm, with transversal t and OQ bisects MNO. If...Ch. 2.1 - Given: lm Transversal t m1=4x+2 m6=4x2 Find: x and...Ch. 2.1 - Given: mn Transversal k m3=x23x m6=(x+4)(x5) Find:...Ch. 2.1 - Given: mn Transversal k m1=5x+y m2=3x+y m8=3x+5y...Ch. 2.1 - Given: mn Transversal k m3=6x+y m5=8x+2y m6=4x+7y...Ch. 2.1 - In the three-dimensional figure, CAAB and BEAB....Ch. 2.1 - Given: lmand34 Prove: 14 See figure below. PROOF...Ch. 2.1 - Given: lmandmn Prove: 14 PROOF Statements Reasons...Ch. 2.1 - Given: CEDF Transversal AB CX bisects ACE DE...Ch. 2.1 - Given: CEDF Transversal AB DE bisects CDF Prove:...Ch. 2.1 - Given: rs Transversal t 1 is a right Prove: 2 is...Ch. 2.1 - Given: ABDEmBAC=42mEDC=54 Find: mACD HINT: There...Ch. 2.1 - Given: ABDEmBAC+mCDE=93 Find: mACD See Hint in...Ch. 2.1 - Prob. 26ECh. 2.1 - In triangle ABC, line t is drawn through vertex A...Ch. 2.1 - In Exercises 30 to 32, write a formal proof of...Ch. 2.1 - In Exercises 30 to 32, write a formal proof of...Ch. 2.1 - In Exercises 30 to 32, write a formal proof of...Ch. 2.1 - Suppose that two lines are cut by a transversal in...Ch. 2.1 - Prob. 32ECh. 2.1 - Prob. 33ECh. 2.1 - Given: Triangle MNQ with obtuse MNQ Construct:...Ch. 2.1 - Prob. 35ECh. 2.1 - Given: A line m and a point T not on m Suppose...Ch. 2.2 - Note: Exercises preceded by an asterisk are of a...Ch. 2.2 - Note: Exercises preceded by an asterisk are of a...Ch. 2.2 - Prob. 3ECh. 2.2 - Note: Exercises preceded by an asterisk are of a...Ch. 2.2 - In Exercises 5 to 10, draw a conclusion where...Ch. 2.2 - Prob. 6ECh. 2.2 - Prob. 7ECh. 2.2 - Prob. 8ECh. 2.2 - Prob. 9ECh. 2.2 - Prob. 10ECh. 2.2 - Which of the following statements would you prove...Ch. 2.2 - Prob. 12ECh. 2.2 - Prob. 13ECh. 2.2 - Prob. 14ECh. 2.2 - Prob. 15ECh. 2.2 - Prob. 16ECh. 2.2 - Prob. 17ECh. 2.2 - Prob. 18ECh. 2.2 - Prob. 19ECh. 2.2 - Prob. 20ECh. 2.2 - A periscope uses an indirect method of...Ch. 2.2 - Some stores use an indirect method of observation....Ch. 2.2 - Prob. 23ECh. 2.2 - Prob. 24ECh. 2.2 - Prob. 25ECh. 2.2 - Prob. 26ECh. 2.2 - In Exercises 23 to 34, give the indirect proof for...Ch. 2.2 - Prob. 28ECh. 2.2 - Prob. 29ECh. 2.2 - Prob. 30ECh. 2.2 - Prob. 31ECh. 2.2 - Prob. 32ECh. 2.2 - Prob. 33ECh. 2.2 - Prob. 34ECh. 2.3 - In Exercises 1 to 6, l and m are cut by...Ch. 2.3 - In Exercises 1 to 6, l and m are cut by...Ch. 2.3 - Prob. 3ECh. 2.3 - In Exercises 1 to 6, l and m are cut by...Ch. 2.3 - In Exercises 1 to 6, l and m are cut by...Ch. 2.3 - In Exercises 1 to 6, l and m are cut by...Ch. 2.3 - In Exercise 7 to 16, name the lines if any that...Ch. 2.3 - In Exercise 7 to 16, name the lines if any that...Ch. 2.3 - In Exercise 7 to 16, name the lines if any that...Ch. 2.3 - In Exercise 7 to 16, name the lines if any that...Ch. 2.3 - In Exercise 7 to 16, name the lines if any that...Ch. 2.3 - In Exercise 7 to 16, name the lines if any that...Ch. 2.3 - In Exercise 7 to 16, name the lines if any that...Ch. 2.3 - In Exercise 7 to 16, name the lines if any that...Ch. 2.3 - In Exercise 7 to 16, name the lines if any that...Ch. 2.3 - In Exercise 7 to 16, name the lines if any that...Ch. 2.3 - Prob. 17ECh. 2.3 - In Exercises 17 and 18, complete each proof by...Ch. 2.3 - In Exercises 19 to 22, complete the proof. Given:...Ch. 2.3 - In Exercise 19 to 22 complete the proof. Given: 1 ...Ch. 2.3 - In Exercise 19 to 22 complete the proof. Given: DE...Ch. 2.3 - In Exercise 19 to 22 complete the proof. Given: XY...Ch. 2.3 - In Exercise 23 to 30, determine the value of x so...Ch. 2.3 - In Exercise 23 to 30, determine the value of x so...Ch. 2.3 - In Exercise 23 to 30, determine the value of x so...Ch. 2.3 - In Exercise 23 to 30, determine the value of x so...Ch. 2.3 - In Exercise 23 to 30, determine the value of x so...Ch. 2.3 - In Exercise 23 to 30, determine the value of x so...Ch. 2.3 - In Exercise 23 to 30, determine the value of x so...Ch. 2.3 - In Exercise 23 to 30, determine the value of x so...Ch. 2.3 - Prob. 31ECh. 2.3 - In Exercises 31 to 33, give a formal proof for...Ch. 2.3 - Prob. 33ECh. 2.3 - Prob. 34ECh. 2.3 - Prob. 35ECh. 2.3 - Prob. 36ECh. 2.3 - Prob. 37ECh. 2.3 - Given: m2+m3=90 BE bisects ABC CE bisects BCD...Ch. 2.4 - In Exercise 1 to 4, refer to ABC . On the basis of...Ch. 2.4 - In Exercise 1 to 4, refer to ABC . On the basis of...Ch. 2.4 - In Exercise 1 to 4, refer to ABC . On the basis of...Ch. 2.4 - In Exercise 1 to 4, refer to ABC . On the basis of...Ch. 2.4 - Describe the auxiliary line segment as determined,...Ch. 2.4 - Describe the auxiliary line segment as determined,...Ch. 2.4 - In Exercises 7 and 8, classify the trianglenot...Ch. 2.4 - In Exercises 7 and 8, classify the trianglenot...Ch. 2.4 - In Exercises 9 and 10, classify the triangle not...Ch. 2.4 - In Exercises 9 and 10, classify the triangle not...Ch. 2.4 - In Exercises 11 and12, make drawings as needed....Ch. 2.4 - In Exercises 11 and 12, make drawings as needed....Ch. 2.4 - In Exercises 13 to 15, jk and ABC. Given:...Ch. 2.4 - In Exercises 13 to 15, jk and ABC. Given:...Ch. 2.4 - In Exercises 13 to 15, jk and. ABC. Given:...Ch. 2.4 - Given: MNNQ and s as shown Find: x, y, and zCh. 2.4 - Given: ABDC DB bisects ADC mA=110 Find: m3Ch. 2.4 - Given: ABDC DB bisects ADC m1=36 Find: mACh. 2.4 - Prob. 19ECh. 2.4 - Given: ABC with BDCE m1=2xm3=x Find: mB in terms...Ch. 2.4 - Given: ADE with m1=m2=x Find: mDAE=x2 x, m1, and...Ch. 2.4 - Given: ABC with mB=mC=x2 Find: mBAC=x x, mBAC, and...Ch. 2.4 - Consider any triangle and one exterior angle at...Ch. 2.4 - Given: Right ABC with right C m1=7x+4m2=5x+2 Find:...Ch. 2.4 - In Exercises 25 to 27 , see the figure for...Ch. 2.4 - In Exercises 25 to 27 , see the figure for...Ch. 2.4 - Prob. 27ECh. 2.4 - Given: m1=8(x+2)m3=5x3m5=5(x+1)2 Find: xCh. 2.4 - Given: Find: , , andCh. 2.4 - Given: Equiangular RST Prove: RV bisects SRT RVS...Ch. 2.4 - Prob. 31ECh. 2.4 - The sum of the measures of two angles of a...Ch. 2.4 - Draw, if possible, an a isosceles obtuse triangle....Ch. 2.4 - Prob. 34ECh. 2.4 - Along a straight shoreline, two houses are located...Ch. 2.4 - An airplane has leveled off is flying horizontally...Ch. 2.4 - Prob. 37ECh. 2.4 - The roofline of a house shows the shape of a right...Ch. 2.4 - A lamppost has design such that mC=110 and AB....Ch. 2.4 - For the lamppost of Exercise 39, Suppose that...Ch. 2.4 - Prob. 41ECh. 2.4 - Prob. 42ECh. 2.4 - Prob. 43ECh. 2.4 - Explain why the following statement is true. The...Ch. 2.4 - Prob. 45ECh. 2.4 - Prob. 46ECh. 2.4 - Prob. 47ECh. 2.4 - Given: AB, DE and CF ABDE CG bisects BCF FG...Ch. 2.4 - Given: NQ bisects MNP PQ bisects MPR mQ=42 Find:...Ch. 2.4 - Prob. 50ECh. 2.5 - For Exercises 1 and 2, consider a group of regular...Ch. 2.5 - For Exercises 1 and 2, consider a group of regular...Ch. 2.5 - Given: ABDC, ADBC, AEFC, with angle measures as...Ch. 2.5 - In pentagon ABCDE with BDE, find the measure of...Ch. 2.5 - Find the total number of diagonals for a polygon...Ch. 2.5 - Find the total number of diagonals for a polygon...Ch. 2.5 - Find the sum of the measures of the interior...Ch. 2.5 - Find the sum of the measures of the interior...Ch. 2.5 - Find the measure of each interior angle of a...Ch. 2.5 - Find the measure of each interior angle of a...Ch. 2.5 - Find the measures of each exterior angle of a...Ch. 2.5 - Find the measures of each exterior angle of a...Ch. 2.5 - Find the number of sides for a polygon whose sum...Ch. 2.5 - Find the number of sides for a polygon whose sum...Ch. 2.5 - Find the number of sides for a regular polygon...Ch. 2.5 - Find the number of sides for a regular polygon...Ch. 2.5 - Find the number of sides for a regular polygon...Ch. 2.5 - Find the number of sides for a regular polygon...Ch. 2.5 - What is the measure of each interior angle of a...Ch. 2.5 - Lug bolts are equally spaced about the wheel to...Ch. 2.5 - Prob. 21ECh. 2.5 - Prob. 22ECh. 2.5 - Prob. 23ECh. 2.5 - Prob. 24ECh. 2.5 - Prob. 25ECh. 2.5 - Prob. 26ECh. 2.5 - Given: Quadrilateral RSTQ with exterior s at R and...Ch. 2.5 - Given: Regular hexagon ABCDEF with diagonal AC and...Ch. 2.5 - Given: Quadrilateral RSTV with diagonals RT and SV...Ch. 2.5 - Given: Quadrilateral ABCD with BAAD and BCDC...Ch. 2.5 - A father wishes to make a baseball home plate for...Ch. 2.5 - The adjacent interior and exterior angles of a...Ch. 2.5 - Find the measure of each a acute interior angle of...Ch. 2.5 - Find the measure of each a acute interior angle of...Ch. 2.5 - Consider any regular polygon; find and join in...Ch. 2.5 - Consider a regular hexagon RSTUVW. What does...Ch. 2.5 - The face of a clock has the shape of a regular...Ch. 2.5 - The top surface of a picnic table is in the shape...Ch. 2.5 - Prob. 39ECh. 2.5 - For the concave quadrilateral ABCD, explain why...Ch. 2.5 - If mA=20, mB=88 and mC=31, find the measure of the...Ch. 2.5 - Is it possible for a polygon to have the following...Ch. 2.5 - Is it possible for a regular polygon to have the...Ch. 2.5 - Draw a concave hexagon that has: a one interior...Ch. 2.5 - Draw a concave pentagon that has: a one interior...Ch. 2.5 - For concave pentagon ABCDE, find the measure of...Ch. 2.5 - For concave hexagon HJKLMN, mH=y and the measure...Ch. 2.6 - Prob. 1ECh. 2.6 - Prob. 2ECh. 2.6 - Prob. 3ECh. 2.6 - Which letters have symmetry with respect to a...Ch. 2.6 - Prob. 5ECh. 2.6 - Prob. 6ECh. 2.6 - Prob. 7ECh. 2.6 - Prob. 8ECh. 2.6 - Prob. 9ECh. 2.6 - Prob. 10ECh. 2.6 - Prob. 11ECh. 2.6 - Prob. 12ECh. 2.6 - Prob. 13ECh. 2.6 - Prob. 14ECh. 2.6 - Prob. 15ECh. 2.6 - Suppose that square RSTV slides point for point to...Ch. 2.6 - Prob. 17ECh. 2.6 - Prob. 18ECh. 2.6 - Prob. 19ECh. 2.6 - Prob. 20ECh. 2.6 - Prob. 21ECh. 2.6 - Prob. 22ECh. 2.6 - In which direction clockwise or counterclockwise...Ch. 2.6 - In which direction clockwise or counterclockwise...Ch. 2.6 - Prob. 25ECh. 2.6 - Prob. 26ECh. 2.6 - Prob. 27ECh. 2.6 - Prob. 28ECh. 2.6 - Prob. 29ECh. 2.6 - Prob. 30ECh. 2.6 - A regular hexagon is rotated about a centrally...Ch. 2.6 - A regular octagon is rotated about a centrally...Ch. 2.6 - Prob. 33ECh. 2.6 - XYZ is the image of XYZ following a 100...Ch. 2.6 - Hexagon ABCBAD is determined when the open figure...Ch. 2.6 - Prob. 36ECh. 2.CR - Prob. 1CRCh. 2.CR - Prob. 2CRCh. 2.CR - Prob. 3CRCh. 2.CR - Prob. 4CRCh. 2.CR - Given: mDCA=130mBAC=2x+ymBCE=150mDEC=2xy Find: x...Ch. 2.CR - Prob. 6CRCh. 2.CR - Prob. 7CRCh. 2.CR - Prob. 8CRCh. 2.CR - For Review Exercises 7 to 11, use the given...Ch. 2.CR - For Review Exercises 7 to 11, use the given...Ch. 2.CR - For Review Exercises 7 to 11, use the given...Ch. 2.CR - Prob. 12CRCh. 2.CR - Prob. 13CRCh. 2.CR - Prob. 14CRCh. 2.CR - For Review Exercises 12 to 15 , find the values of...Ch. 2.CR - Given: m1=x212 m4=x(x2) Find: x so that ABCDCh. 2.CR - Prob. 17CRCh. 2.CR - Prob. 18CRCh. 2.CR - Prob. 19CRCh. 2.CR - For Review Exercises 19 to 24, decide whether the...Ch. 2.CR - Prob. 21CRCh. 2.CR - Prob. 22CRCh. 2.CR - Prob. 23CRCh. 2.CR - Prob. 24CRCh. 2.CR - Complete the following table for regular polygons....Ch. 2.CR - Prob. 26CRCh. 2.CR - For Review Exercises 26 to 29, sketch, if...Ch. 2.CR - For Review Exercises 26 to 29, sketch, if...Ch. 2.CR - Prob. 29CRCh. 2.CR - For Review Exercises 30 and 31, write the...Ch. 2.CR - For Review Exercises 30 and 31, write the...Ch. 2.CR - Which statementthe converse, the inverse, or the...Ch. 2.CR - Given: ABCF23 Prove: 13Ch. 2.CR - Given: 1 is complementary to 2; 2 is complementary...Ch. 2.CR - Prob. 35CRCh. 2.CR - Given: ACDCAB Prove: DACBCh. 2.CR - Prob. 37CRCh. 2.CR - Prob. 38CRCh. 2.CR - Prob. 39CRCh. 2.CR - Prob. 40CRCh. 2.CR - Prob. 41CRCh. 2.CR - Construct an equilateral triangle ABC with side...Ch. 2.CR - Prob. 43CRCh. 2.CR - Prob. 44CRCh. 2.CR - Prob. 45CRCh. 2.CR - Complete the drawing so that the figure is...Ch. 2.CR - Prob. 47CRCh. 2.CT - Consider the figure shown at the right. a Name the...Ch. 2.CT - In the accompanying figure, m2=68, m8=112, and...Ch. 2.CT - To prove a theorem of the form "If P, then Q" by...Ch. 2.CT - Assuming that statements 1 and 2 are true, draw a...Ch. 2.CT - Let all of the lines named be coplanar. Make a...Ch. 2.CT - Prob. 6CTCh. 2.CT - Prob. 7CTCh. 2.CT - Prob. 8CTCh. 2.CT - Prob. 9CTCh. 2.CT - Prob. 10CTCh. 2.CT - Prob. 11CTCh. 2.CT - Prob. 12CTCh. 2.CT - Prob. 13CTCh. 2.CT - Prob. 14CTCh. 2.CT - Prob. 15CTCh. 2.CT - In Exercises 16 and 18 , complete the missing...Ch. 2.CT - Prob. 17CTCh. 2.CT - Prob. 18CTCh. 2.CT - Prob. 19CT
Knowledge Booster
Background pattern image
Geometry
Learn more about
Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, geometry and related others by exploring similar questions and additional content below.
Similar questions
SEE MORE QUESTIONS
Recommended textbooks for you
Text book image
Elementary Geometry for College Students
Geometry
ISBN:9781285195698
Author:Daniel C. Alexander, Geralyn M. Koeberlein
Publisher:Cengage Learning
Text book image
Elementary Geometry For College Students, 7e
Geometry
ISBN:9781337614085
Author:Alexander, Daniel C.; Koeberlein, Geralyn M.
Publisher:Cengage,
Text book image
Mathematics For Machine Technology
Advanced Math
ISBN:9781337798310
Author:Peterson, John.
Publisher:Cengage Learning,
SEE MORE TEXTBOOKS
Sequences and Series Introduction; Author: Mario's Math Tutoring;https://www.youtube.com/watch?v=m5Yn4BdpOV0;License: Standard YouTube License, CC-BY
Introduction to sequences; Author: Dr. Trefor Bazett;https://www.youtube.com/watch?v=VG9ft4_dK24;License: Standard YouTube License, CC-BY