Chapter 29, Problem 7P

To determine

To calculate: The temperature on the heated plate with fixed temperature at the boundaries and round corners at upper right and lower left corners; considering the value of weighing factor for overrelaxation as 1.5 and performing iteration up to ${\epsilon }_s=1\%$.

Answer to Problem 7P

Solution:

Heated plate having rounded upper right and lower left corners has the temperature distribution with the desired level of accuracy as,

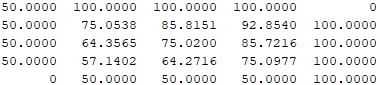
Explanation of Solution

Given Information:

The fixed temperature at top and right boundary is $100°\text{C}$ and the fixed temperature at the left and lower boundary is $50°\text{C}$.

For overrelaxation the weighing factor is 1.5.

Limiting condition for iteration is ${\epsilon }_s\le 1\%$

Formula used:

For a square grid, that is, $\Delta x=\Delta y$, the Laplacian difference equation is written using Liebmann’s method as,

$T_{i,j}=\frac{T_{i+1,j}+T_{i-1,j}+T_{i,j+1}+T_{i,j-1}}{4}$

With $i$ varying from 1 to m and $j$ varying from 1 to n.

Overrelaxation is applied using the following expression after each iteration,

$T_{i,j}^{new}=\lambda T_{i,j}^{new}+\left(1-\lambda \right)T_{i,j}^{old}$

In the above expression, $T_{i,j}^{old}$ and $T_{i,j}^{new}$ being the $T_{i,j}$ values from the previous and present iteration.

The percent relative error is calculated using the following expression,

$\left|{\left({\epsilon }_a\right)}_{i,j}\right|=\left(\left|\frac{T_{i,j}^{new}-T_{i,j}^{old}}{T_{i,j}^{new}}\right|\times 100\right)\%$

Laplacian equation for a node adjacent to an irregular boundary is solved for temperature distribution as,

$\frac{2}{\Delta x^2}\left[\frac{T_{i-1,j}-T_{i,j}}{{\alpha }_1\left({\alpha }_1+{\alpha }_2\right)}+\frac{T_{i+1,j}-T_{i,j}}{{\alpha }_2\left({\alpha }_1+{\alpha }_2\right)}\right]+\frac{2}{\Delta y^2}\left[\frac{T_{i,j-1}-T_{i,j}}{{\beta }_1\left({\beta }_1+{\beta }_2\right)}+\frac{T_{i,j+1}-T_{i,j}}{{\beta }_2\left({\beta }_1+{\beta }_2\right)}\right]=0$

Calculation:

Consider, $\Delta x=\Delta y$.

Consider the value of the parameters as,

$\begin{array}{l}{\alpha }_1=0.732\\ {\alpha }_2=1\\ {\beta }_1=0.732\\ {\beta }_2=1\end{array}$

The temperature at the node $\left(4,2\right)$ adjacent to the lower left round corner or the irregular boundary is calculated as,

$\begin{array}{c}\frac{2}{\Delta x^2}\left[\frac{T_{3,2}-T_{4,2}}{0.732\left(0.732+1\right)}+\frac{T_{5,2}-T_{4,2}}{1\left(0.732+1\right)}\right]+\frac{2}{\Delta y^2}\left[\frac{T_{4,1}-T_{4,2}}{0.732\left(0.732+1\right)}+\frac{T_{4,3}-T_{4,2}}{1\left(0.732+1\right)}\right]=0\\ \left[\frac{T_{3,2}-T_{4,2}}{0.732\left(0.732+1\right)}+\frac{T_{5,2}-T_{4,2}}{1\left(0.732+1\right)}\right]+\left[\frac{T_{4,1}-T_{4,2}}{0.732\left(0.732+1\right)}+\frac{T_{4,3}-T_{4,2}}{1\left(0.732+1\right)}\right]=0\end{array}$

Thus,

$-4T_{4,2}+0.8453T_{5,2}+0.8453T_{4,3}=-1.1547\left(T_{3,2}+T_{4,1}\right)$

Further, the temperature at the node $\left(2,4\right)$ adjacent to the upper right round corner or the irregular boundary is calculated as,

$\begin{array}{c}\frac{2}{\Delta x^2}\left[\frac{T_{1,4}-T_{2,4}}{0.732\left(0.732+1\right)}+\frac{T_{3,4}-T_{2,4}}{1\left(0.732+1\right)}\right]+\frac{2}{\Delta y^2}\left[\frac{T_{2,3}-T_{2,4}}{0.732\left(0.732+1\right)}+\frac{T_{2,5}-T_{2,4}}{1\left(0.732+1\right)}\right]=0\\ \left[\frac{T_{1,4}-T_{2,4}}{0.732\left(0.732+1\right)}+\frac{T_{3,4}-T_{2,4}}{1\left(0.732+1\right)}\right]+\left[\frac{T_{2,3}-T_{2,4}}{0.732\left(0.732+1\right)}+\frac{T_{2,5}-T_{2,4}}{1\left(0.732+1\right)}\right]=0\end{array}$

Thus,

$-4T_{2,4}+0.8453T_{3,4}+0.8453T_{2,5}=-1.1547\left(T_{1,4}+T_{2,3}\right)$

Liebmann’s method is used to solve the temperature on the heated plate iteratively in MATLAB, until the percent relative error falls below 1%.

Use the following MATLAB code to implement the Liebmann’s method and the equation at the nodes $\left(4,2\right)\&\left(2,4\right)$ to solve for the temperature distribution on the heated plate with fixed boundary conditions as,

clear;clc;

% Enter the initial temperature distribution

T = zeros(5,5);

% Enter the initial conditions

T(1,1:4) = 100;

T(2:5,5) = 100;

T(5,2:4) = 50;

T(1:4,1) = 50;

ans

n = length(T(:,1));

m = length(T(1,:));

% Enter the Weighing factor

lambda = 1.5;

iteration = 0;

A = ((1/(0.732*1.732))*2/((1/(0.732*1.732))+(1/(1.732))));

B = ((1/(1.732))*2/((1/(0.732*1.732))+(1/(1.732))));

% Start the loop and run it until Ea < 1

while 1

for i = 2:m-1

for j = 2:n-1

Told(i,j) = T(i,j);

% for lower left and upper right corner nodes

if (i == 4 && j == 2) || (i == 2 && j == 4)

T(i,j) = (-(A*(T(i-1,j)+T(i,j-1)))-(B*T(i+1,j))...

-(B*T(i,j+1)))/(-4);

else

% Liebmann's method for rest of the interior nodes

T(i,j) = (T(i+1,j)+T(i-1,j)+T(i,j+1)+T(i,j-1))/4;

% Percent relative error

Ea(i,j) = abs((T(i,j)-Told(i,j))/T(i,j))*100;

T(i,j) = (lambda*T(i,j))+((1-lambda)*Told(i,j));

end

end

end

iteration = iteration+1;

if max(Ea(:,:)) < 1

break

end

end

T

iteration

Execute the above code to obtain the temperature distribution and the number of iterations performed, in the output as shown below,

T =

50.0000 100.0000 100.0000 100.0000 0

50.0000 75.0538 85.8151 92.8540 100.0000

50.0000 64.3565 75.0200 85.7216 100.0000

50.0000 57.1402 64.2716 75.0977 100.0000

0 50.0000 50.0000 50.0000 100.0000

iteration =

9

Hence, the temperature on the heated plate with desired accuracy is achieved after 9 iterations as obtained in the above MATLAB output.