Applied Physics (11th Edition)
11th Edition
ISBN: 9780134159386
Author: Dale Ewen, Neill Schurter, Erik Gundersen
Publisher: PEARSON
expand_more
expand_more
format_list_bulleted
Concept explainers
Videos
Textbook Question
Chapter 3, Problem 1AC
The New Clark Bridge is an elegant cable-stayed Bridge. Its design requires cables to reach from the road deck up to the tower and back down to the road deck on the other side of the tower, as shown in Fig. 3.41. In order to determine the best method for shipping the cables, the shipping company needs to know the lengths of the shortest and longest cables. Given the measurements in the diagram, determine the indicated total lengths BEC and AED, respectively.
Tower's height above the road deck = 176 ft
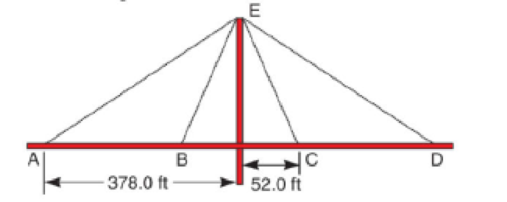
Figure 3.41
Expert Solution & Answer
Want to see the full answer?
Check out a sample textbook solution
Students have asked these similar questions
STUDENT SCREEN P
%3B
图
23. A climber is on a hike. After 180
24. Ms
minutes, he is at an altitude of 400
feet. After 360 minutes, he is at an
altitude of 700 feet. Write the
equation of the line that represents
this relationship if y is the altitude and
x is the time.
BAMS
also a
ougt
This r
for $5
repre
sani
the
The radius of an atom of gold (Au) is about 1.35 Å.
How many gold atoms would have to be lined up to span 4.0 mm? Express your answer using two significant figures.
The number of viruses (V , measured in trillions or 10¹²) that infect a person is a function of the degree of immunosuppression (I, the fraction of the immune system that is turned off by stress) according to V(I) = 5I². The fever (F, measured in ◦C) associated with an infection is a function of the number of viruses according to F(V) = 37 + 0.4V. Find fever as a function of immunosuppression. How high will the fever be if immunosuppression is complete (I = 1)?
Chapter 3 Solutions
Applied Physics (11th Edition)
Ch. 3.1 - Using the scale 1.0 cm = 50km, find the length of...Ch. 3.1 - Using the scale 1.0 cm = 50km, find the length of...Ch. 3.1 - Using the scale 1.0 cm = 50km, find the length of...Ch. 3.1 - Using the scale 1.0 cm = 50km, find the length of...Ch. 3.1 - Using the scale 1.0 cm = 50km, find the length of...Ch. 3.1 - Using the scale 1.0 cm = 50km, find the length of...Ch. 3.1 - Draw the vectors in Problems 1 through 6 using the...Ch. 3.1 - Draw the vectors in Problems 1 through 6 using the...Ch. 3.1 - Draw the vectors in Problems 1 through 6 using the...Ch. 3.1 - Draw the vectors in Problems 1 through 6 using the...
Ch. 3.1 - Draw the vectors in Problems 1 through 6 using the...Ch. 3.1 - Draw the vectors in Problems 1 through 6 using the...Ch. 3.1 - Using the scale 14 in. = 20 mi, find the length of...Ch. 3.1 - Using the scale 14 in. = 20 mi, find the length of...Ch. 3.1 - Using the scale 14 in. = 20 mi, find the length of...Ch. 3.1 - Using the scale 14 in. = 20 mi, find the length of...Ch. 3.1 - Using the scale 14 in. = 20 mi, find the length of...Ch. 3.1 - Using the scale 14 in. = 20 mi, find the length of...Ch. 3.1 - Draw the vectors in Problems 13 through 18 using...Ch. 3.1 - Draw the vectors in Problems 13 through 18 using...Ch. 3.1 - Draw the vectors in Problems 13 through 18 using...Ch. 3.1 - Draw the vectors in Problems 13 through 18 using...Ch. 3.1 - Draw the vectors in Problems 13 through 18 using...Ch. 3.1 - Draw the vectors in Problems 13 through 18 using...Ch. 3.2 - Find the x- and y-components of each vector in the...Ch. 3.2 - Find the x- and y-components of each vector in the...Ch. 3.2 - Find the x- and y-components of each vector in the...Ch. 3.2 - Find the x- and y-components of each vector in the...Ch. 3.2 - Find the x- and y-components of each vector in the...Ch. 3.2 - Find the x- and y-components of each vector in the...Ch. 3.2 - Find the x- and y-components of each vector in the...Ch. 3.2 - Find the x- and y-components of each vector in the...Ch. 3.2 - Find the x- and y-components of each vector in the...Ch. 3.2 - Find the x- and y-components of each vector in the...Ch. 3.2 - Make a sketch of each vector in standard position....Ch. 3.2 - Make a sketch of each vector in standard position....Ch. 3.2 - Make a sketch of each vector in standard position....Ch. 3.2 - Make a sketch of each vector in standard position....Ch. 3.2 - Make a sketch of each vector in standard position....Ch. 3.2 - Make a sketch of each vector in standard position....Ch. 3.2 - Make a sketch of each vector in standard position....Ch. 3.2 - Make a sketch of each vector in standard position....Ch. 3.2 - Find the x- and y- components of each vector. 19.Ch. 3.2 - Find the x- and y- components of each vector. 20.Ch. 3.2 - Find the x- and y- components of each vector. 21.Ch. 3.2 - Find the x- and y- components of each vector. 22.Ch. 3.2 - Find the x- and y- components of each vector. 23.Ch. 3.2 - Find the x- and y- components of each vector. 24.Ch. 3.2 - Find the x- and y-components of each vector given...Ch. 3.2 - Find the x- and y-components of each vector given...Ch. 3.2 - Find the x- and y-components of each vector given...Ch. 3.2 - Find the x- and y-components of each vector given...Ch. 3.2 - Find the x- and y-components of each vector given...Ch. 3.2 - Find the x- and y-components of each vector given...Ch. 3.3 - Use graph paper to find the resultant of each...Ch. 3.3 - Use graph paper to find the resultant of each...Ch. 3.3 - Use graph paper to find the resultant of each...Ch. 3.3 - Use graph paper to find the resultant of each...Ch. 3.3 - Use graph paper to find the resultant of each...Ch. 3.3 - Use graph paper to find the resultant of each...Ch. 3.3 - Use graph paper to find the resultant of each...Ch. 3.3 - Use graph paper to find the resultant of each...Ch. 3.3 - Use graph paper to find the resultant of each...Ch. 3.3 - Use graph paper to find the resultant or each...Ch. 3.3 - Use graph paper to find the resultant or each...Ch. 3.3 - Use graph paper to find the resultant of each...Ch. 3.3 - Use graph paper to find the resultant of each...Ch. 3.3 - Use graph paper to find the resultant of each...Ch. 3.3 - Find the x- and y- components of each resultant...Ch. 3.3 - Find the x- and y- components of each resultant...Ch. 3.3 - Find the x- and y- components of each resultant...Ch. 3.3 - Find the x- and y- components of each resultant...Ch. 3.3 - Find the x- and y- components of each resultant...Ch. 3.3 - Find the x- and y- components of each resultant...Ch. 3.3 - Find the x- and y- components of each resultant...Ch. 3.3 - Find the x- and y- components of each resultant...Ch. 3.3 - Find the x- and y- components of each resultant...Ch. 3.3 - Find the x- and y- components of each resultant...Ch. 3.3 - For each set of vectors, graph and find the x- and...Ch. 3.3 - For each set of vectors, graph and find the x- and...Ch. 3.3 - For each set of vectors, graph and find the x- and...Ch. 3.3 - For each set of vectors, graph and find the x- and...Ch. 3.3 - For each set of vectors, graph and find the x- and...Ch. 3.3 - For each set of vectors, graph and find the x- and...Ch. 3.3 - In Problems 31 through 42, find each resultant...Ch. 3.3 - In Problems 31 through 42, find each resultant...Ch. 3.3 - In Problems 31 through 42, find each resultant...Ch. 3.3 - In Problems 31 through 42, find each resultant...Ch. 3.3 - In Problems 31 through 42, find each resultant...Ch. 3.3 - In Problems 31 through 42, rind each resultant...Ch. 3.3 - In Problems 31 through 42, find each resultant...Ch. 3.3 - In Problems 31 through 42, find each resultant...Ch. 3.3 - In Problems 31 through 42, find each resultant...Ch. 3.3 - In Problems 31 through 42, find each resultant...Ch. 3.3 - In Problems 31 through 42, find each resultant...Ch. 3.3 - In Problems 31 through 42, find each resultant...Ch. 3.3 - A road grader must go around a pond by traveling...Ch. 3.3 - An earthmover must go north 350 m and then west...Ch. 3.3 - An airplane takes off and flies 225 km on a course...Ch. 3.3 - A ship travels 50.0 mi on a course of 15.0 south...Ch. 3.3 - A ship travels 135 km from port on a course of...Ch. 3.3 - A ship travels 145 km from port on a course of...Ch. 3 - Displacement a. can be interchanged with...Ch. 3 - When adding vectors, the order in which they are...Ch. 3 - A vector is in standard position when its initial...Ch. 3 - Discuss number plane, origin, and axis in your own...Ch. 3 - Can every vector be described in terms of its...Ch. 3 - Describe how to add two or more vectors...Ch. 3 - Describe how to find a resultant vector if given...Ch. 3 - Is a vector limited to a single position in the...Ch. 3 - Is the angle of a vector in standard position...Ch. 3 - What are the limits on the angle measure of a...Ch. 3 - Describe how to find the x- and y-components of a...Ch. 3 - Describe how to find a vector in standard position...Ch. 3 - Find the x- and y-components of vector R, which...Ch. 3 - Find the x- and y-components of vector R, which...Ch. 3 - Find the x- and y-components of vector R, which...Ch. 3 - Vector R has length 9.00 cm at 240.0. Find its x-...Ch. 3 - Vector R has length 9.00 cm at 40.0. Find its x-...Ch. 3 - Vector R has length 18.0 cm at 305.0. Find its x-...Ch. 3 - A hiker is plotting his course on a map with a...Ch. 3 - A hiker is plotting his course on a map with a...Ch. 3 - A co-pilot is charting her course on a map with a...Ch. 3 - A co-pilot is charting her course on a map with a...Ch. 3 - Vector R has x-component = +14.0 and y-component =...Ch. 3 - Vector R has x-component = -5.00 and y-component =...Ch. 3 - Vector R has x-component = +8.00 and y-component =...Ch. 3 - Vector R has x-component = -3.00 and y-component =...Ch. 3 - Vectors A, B, and C are given. Vector A has...Ch. 3 - Vectors A, B, and C are given. Vector A has...Ch. 3 - Vectors A, B. and C are given. Vector A has...Ch. 3 - Vectors A, B, and C are given. Vector A has...Ch. 3 - Graph and find x- and y-components of each...Ch. 3 - Graph and find the x- and y-components of each...Ch. 3 - An airplane takes off and flies 245 km on a course...Ch. 3 - A ship travels 155 km from port on a course of...Ch. 3 - The New Clark Bridge is an elegant cable-stayed...Ch. 3 - Frank just learned that the 800-m section of...Ch. 3 - Power cables need to be suspended by the power...Ch. 3 - With the airplane cruising at 30,000 ft, the...
Additional Science Textbook Solutions
Find more solutions based on key concepts
3. Does a good insulator prevent heat from getting through it, or does it simply delay its passage?
Conceptual Physical Science (6th Edition)
The pV-diagram of the Carnot cycle.
Sears And Zemansky's University Physics With Modern Physics
A system consisting of 20.0 mol of a monoatomic ideal gas is cooled at constant pressure from a volume of 50.0 ...
University Physics Volume 2
The volume of blood that flows per second through the pulmonary artery.
Physics (5th Edition)
Find expressions for the force needed to bring an object of mass m from rest to speed v (a) in lime t and (b) o...
Essential University Physics: Volume 1 (3rd Edition)
E. Suppose you selected two widely separated dots on the ticker tape assembled in part B. What would you call t...
Tutorials in Introductory Physics
Knowledge Booster
Learn more about
Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, physics and related others by exploring similar questions and additional content below.Similar questions
- Three displacement vectors of a croquet ball are shown in Figure P1.44, where |A|=20.0units, |B|=40.0units, and |C|=30.0units. Find (a) the resultant in unit-vector notation and (b) the magnitude and direction of the resultant displacement. Figure P1.44arrow_forwardA skater glides along a circular path of radius 5.00 m in clockwise direction. ‘When he coasts around one- half of the circle, starting from the west point, find (a) the magnitude of his displacement vector and (b) how far he actually skated. (c) What is the magnitude of his displacement vector when he skates all the way around the circle and comes back to the west point?arrow_forwardA sidewalk is to be constructed around a swimming pool that measures (10.0 0.1) m by (17.0 0.1) m. If the sidewalk is to measure (1.00 0.01) m wide by (9.0 0.1) cm thick, what volume of concrete is needed and what is the approximate uncertainty of this volume?arrow_forward
- A person going for a walk follows the path shown in Figure P1.51. The total trip consists of four straight-line paths. At the end of the walk, what is the persons resultant displacement measured from the starting point? Figure P1.51arrow_forwardThe common Eastern mole, a mammal, typically has a mass of 75 g, which corresponds to about 7.5 moles of atoms. (A mole of atoms is 6.02 * 1023 atoms.) In atomic mass units (u), what is the average mass of the atoms in the common Eastern mole?arrow_forwardYou want to calculate the area of your dorm room which is in a rectangular shape. You measure the length and the width of the room as L = 5.8 +- 0.1 m , W = 3.5 +- 0.1 m. What is the absolute error in the area in m2 units?arrow_forward
- ANSWER: 1.60 Please show all the steps and the equation required in each situation.arrow_forwardIn astronomy, a unit of distance is used called the Astronomical Unit. It is the average distance from the Earth to the Sun. If 1 au is 1.49 × 1011 m, and a light-year is the distance it takes light to travel in 1 year elapsed time (light travels at a speed of c = 3.0 x 108 ), then how many au is it to get to Alpha Centauri (our closest star with a planetary system) if is 4.367 lightyears away?arrow_forwardHow many nanoseconds does it take light to travel 1.00 ft in vacuum? (This result is a useful quantity to remember.)arrow_forward
arrow_back_ios
SEE MORE QUESTIONS
arrow_forward_ios
Recommended textbooks for you
Principles of Physics: A Calculus-Based TextPhysicsISBN:9781133104261Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning
University Physics Volume 1PhysicsISBN:9781938168277Author:William Moebs, Samuel J. Ling, Jeff SannyPublisher:OpenStax - Rice University
Classical Dynamics of Particles and SystemsPhysicsISBN:9780534408961Author:Stephen T. Thornton, Jerry B. MarionPublisher:Cengage Learning
College PhysicsPhysicsISBN:9781305952300Author:Raymond A. Serway, Chris VuillePublisher:Cengage Learning
An Introduction to Physical SciencePhysicsISBN:9781305079137Author:James Shipman, Jerry D. Wilson, Charles A. Higgins, Omar TorresPublisher:Cengage Learning
Principles of Physics: A Calculus-Based Text
Physics
ISBN:9781133104261
Author:Raymond A. Serway, John W. Jewett
Publisher:Cengage Learning
University Physics Volume 1
Physics
ISBN:9781938168277
Author:William Moebs, Samuel J. Ling, Jeff Sanny
Publisher:OpenStax - Rice University
Classical Dynamics of Particles and Systems
Physics
ISBN:9780534408961
Author:Stephen T. Thornton, Jerry B. Marion
Publisher:Cengage Learning
College Physics
Physics
ISBN:9781305952300
Author:Raymond A. Serway, Chris Vuille
Publisher:Cengage Learning
An Introduction to Physical Science
Physics
ISBN:9781305079137
Author:James Shipman, Jerry D. Wilson, Charles A. Higgins, Omar Torres
Publisher:Cengage Learning
Introduction to Vectors and Their Operations; Author: Professor Dave Explains;https://www.youtube.com/watch?v=KBSCMTYaH1s;License: Standard YouTube License, CC-BY