
Calculus: Early Transcendentals
8th Edition
ISBN: 9781285741550
Author: James Stewart
Publisher: Cengage Learning
expand_more
expand_more
format_list_bulleted
Concept explainers
Textbook Question
Chapter 3.7, Problem 6E
Graphs of the position functions of two particles are shown, where 1 is measured in seconds. When is each particle speeding up? When is it slowing down? Explain.
(a)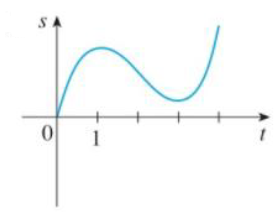
(b)
Expert Solution & Answer
Want to see the full answer?
Check out a sample textbook solution
Chapter 3 Solutions
Calculus: Early Transcendentals
Ch. 3.1 - (a) How is the number e defined? (b) Use a...Ch. 3.1 - (a) Sketch, by hand, the graph of the function...Ch. 3.1 - Differentiate the function. f(x) = 240Ch. 3.1 - Differentiate the function. f(x) = e5Ch. 3.1 - Differentiate the function. f(x) = 5.2x + 2.3Ch. 3.1 - Differentiate the function. g(x)=74x23x+12Ch. 3.1 - Differentiate the function. f(t) = 2t3 3t2 4tCh. 3.1 - Differentiate the function. f(t) = 1.4t5 2.5t2+...Ch. 3.1 - Differentiate the function. g(x) = x2(1 2x)Ch. 3.1 - Differentiate the function. H(u) = (3u 1)(u + 2)
Ch. 3.1 - Differentiate the function. g(t) = 2t3/4Ch. 3.1 - Differentiate the function. B(y) = cy6Ch. 3.1 - Differentiate the function. F(r)=5r3Ch. 3.1 - Differentiate the function. y = x5/3 x2/3Ch. 3.1 - Differentiate the function. R(a) = (3a + 1)2Ch. 3.1 - Differentiate the function. h(t)=t44etCh. 3.1 - Differentiate the function. S(p)=ppCh. 3.1 - Differentiate the function. y=x3(2+x)Ch. 3.1 - Differentiate the function. y=3ex+4x3Ch. 3.1 - Differentiate the function. S(R) = 4R2Ch. 3.1 - Differentiate the function. h(u)=Au3+Bu2+CuCh. 3.1 - Differentiate the function. y=x+xx2Ch. 3.1 - Differentiate the function. y=x2+4x+3xCh. 3.1 - Differentiate the function. G(t)=5t+7tCh. 3.1 - Differentiate the function. j(x) = x2.4 + e2.4Ch. 3.1 - Differentiate the function. k(r) = er + reCh. 3.1 - Differentiate the function. G(q) = (1 + q1)2Ch. 3.1 - Differentiate the function. F(z)=A+Bz+Cz2z2Ch. 3.1 - Differentiate the function. f(v)=v32vevvCh. 3.1 - Differentiate the function. D(t)=1+16t2(4t)3Ch. 3.1 - Differentiate the function. z=Ay10+BeyCh. 3.1 - Differentiate the function. y = ex + 1 + 1Ch. 3.1 - Find an equation of the tangent line to the curve...Ch. 3.1 - Find an equation of the tangent line to the curve...Ch. 3.1 - Find an equation of the tangent line to the curve...Ch. 3.1 - Find an equation of the tangent line to the curve...Ch. 3.1 - Find equations of the tangent line and normal line...Ch. 3.1 - Find equations of the tangent line and normal line...Ch. 3.1 - Find an equation of the tangent line to the curve...Ch. 3.1 - Find an equation of the tangent line to the curve...Ch. 3.1 - Find f'(x). Compare the graphs of f and f' and use...Ch. 3.1 - Find f'(x). Compare the graphs of f and f' and use...Ch. 3.1 - Prob. 43ECh. 3.1 - Prob. 44ECh. 3.1 - Find the first and second derivatives of the...Ch. 3.1 - Find the first and second derivatives of the...Ch. 3.1 - Find the first and second derivatives of the...Ch. 3.1 - Find the first and second derivatives of the...Ch. 3.1 - The equation of motion of a particle is s = t3 ...Ch. 3.1 - The equation of motion of a particle is s = t4 ...Ch. 3.1 - Biologists have proposed a cubic polynomial to...Ch. 3.1 - The number of tree species S in a given area A in...Ch. 3.1 - Boyles Law states that when a sample of gas is...Ch. 3.1 - Find the points on the curve y = 2x3 + 3x2 12x +...Ch. 3.1 - For what value of x does the graph of f(x) = ex ...Ch. 3.1 - Show that the curve y = 2ex + 3x + 5x3 has no...Ch. 3.1 - Find an equation of the tangent line to the curve...Ch. 3.1 - Find equations of both lines that are tangent to...Ch. 3.1 - At what point on the curve y = 1 + 2ex 3x is the...Ch. 3.1 - Find an equation of the normal line to the curve...Ch. 3.1 - Where does the normal line to the parabola y = x2 ...Ch. 3.1 - Draw a diagram to show that there are two tangent...Ch. 3.1 - (a) Find equations of both lines through the point...Ch. 3.1 - Use the definition of a derivative to show that if...Ch. 3.1 - Find the nth derivative of each function by...Ch. 3.1 - Find a second-degree polynomial P such that P(2) =...Ch. 3.1 - The equation y" + y' 2y = x2 is called a...Ch. 3.1 - Find a cubic function y = ax3 + bx2 + cx + d whose...Ch. 3.1 - Find a parabola with equation y = ax2 + bx + c...Ch. 3.1 - Let {x2+1ifx1x+1ifx1 Is f differentiable at 1?...Ch. 3.1 - At what numbers is the following function g...Ch. 3.1 - (a) For what values of x is the function f(x) =...Ch. 3.1 - Where is the function h(x) = |x 1| + |x + 2|...Ch. 3.1 - Find the parabola with equation y = ax2 + bx whose...Ch. 3.1 - Suppose the curve y = x4 + ax3 + bx2 + cx + d has...Ch. 3.1 - For what values of a and b is the line 2x + y = b...Ch. 3.1 - Prob. 78ECh. 3.1 - What is the value of c such that the line y = 2x +...Ch. 3.1 - The graph of any quadratic function f(x) = ax2 +...Ch. 3.1 - Let f(x){x2ifx2mx+bifx2 Find the values of m and b...Ch. 3.1 - Prob. 82ECh. 3.1 - Prob. 83ECh. 3.1 - Prob. 84ECh. 3.1 - If c12, how many lines through the point (0, c)...Ch. 3.1 - Prob. 86ECh. 3.2 - Find the derivative of f(x) = (1 + 2x2)(x x2) in...Ch. 3.2 - Find the derivative o f the function...Ch. 3.2 - Differentiate. f(x) = (3x2 5x)exCh. 3.2 - 4. Differentiate. g(x)=(x+2x)exCh. 3.2 - Differentiate. y=xexCh. 3.2 - Differentiate. y=ex1exCh. 3.2 - Differentiate. g(x)=1+2x34xCh. 3.2 - Differentiate. G(x)=x222x+1Ch. 3.2 - Differentiate. H(u)=(uu)(u+u)Ch. 3.2 - Differentiate. J(v) = (v3 2v)(v4 + v2)Ch. 3.2 - Prob. 11ECh. 3.2 - Differentiate. f(z) = (1 ez)(z + ez)Ch. 3.2 - Differentiate. y=x2+1x31Ch. 3.2 - Prob. 14ECh. 3.2 - Differentiate. y=t3+3tt24t+3Ch. 3.2 - Differentiate. y=1t3+2t21Ch. 3.2 - Differentiate. y=ep(p+pp)Ch. 3.2 - Differentiate. h(r)=aerb+erCh. 3.2 - Differentiate. y=sss2Ch. 3.2 - Prob. 20ECh. 3.2 - Differentiate. f(t)=t3t3Ch. 3.2 - Differentiate. V(t)=4+ttetCh. 3.2 - Differentiate. f(x)=x2exx2+exCh. 3.2 - Prob. 24ECh. 3.2 - Differentiate. f(x)=xx+cxCh. 3.2 - Differentiate. f(x)=ax+bcx+dCh. 3.2 - Find f'(x) and f"(x). f(x) = (x3 + 1)exCh. 3.2 - Find f'(x) and f"(x). f(x)=xexCh. 3.2 - Find f'(x) and f"(x). f(x)=x21+exCh. 3.2 - Find f'(x) and f"(x). f(x)=xx21Ch. 3.2 - Find an equation of the tangent line to the given...Ch. 3.2 - Find an equation of the tangent line to the given...Ch. 3.2 - Find equations of the tangent line and normal line...Ch. 3.2 - Find equations of the tangent line and normal line...Ch. 3.2 - (a) The curve y = 1/(1 + x2) is called a witch of...Ch. 3.2 - (a) The curve y = x/(1 + x2) is called a...Ch. 3.2 - (a) If f(x) = (x3 x)ex, find f'(x). (b) Check to...Ch. 3.2 - Prob. 38ECh. 3.2 - (a) If f(x) = (x2 1)/(x2 + 1), find f'(x) and...Ch. 3.2 - (a) If f(x) = (x2 1)ex, find f'(x) and f"(x). (b)...Ch. 3.2 - If f(x) = x2/(l + x), find f"(1).Ch. 3.2 - If g(x) = x/ex. find g(n)(x).Ch. 3.2 - Suppose that f(5) = 1, f'(5) = 6, g(5) = 3, and...Ch. 3.2 - Suppose that f(4) = 2, g(4) = 5, f'(4) = 6. and...Ch. 3.2 - If f(x) = exg(x), where g(0) = 2 and g'(0) = 5,...Ch. 3.2 - If h(2) = 4 and h'(2) = 3, find ddx(h(x)x)|x=2Ch. 3.2 - If g(x) = xf(x), where f(3) = 4 and f'(3) = 2,...Ch. 3.2 - If f(2) = 10 and f'(x) = x2f(x) for all x, find...Ch. 3.2 - If f and g are the functions whose graphs are...Ch. 3.2 - Let P(x) = F(x)G(x) and Q(x) = F(x)/G(x), where F...Ch. 3.2 - If g is a differentiable function, find an...Ch. 3.2 - If f is a differentiable function, find an...Ch. 3.2 - How many tangent lines to the curve y = x/(x + 1)...Ch. 3.2 - Find equations of the tangent lines to the curve...Ch. 3.2 - Find R'(0), where R(x)=x3x3+5x51+3x3+6x6+9x9 Hint:...Ch. 3.2 - Use the method of Exercise 55 to compute Q'(0),...Ch. 3.2 - In this exercise we estimate the rate at which the...Ch. 3.2 - A manufacturer produces bolts of a fabric with a...Ch. 3.2 - The Michaelis-Menten equation for the enzyme...Ch. 3.2 - Prob. 60ECh. 3.2 - (a) Use the Product Rule twice to prove that if f,...Ch. 3.2 - (a) If F(x) = f(x) g(x), where f and g have...Ch. 3.2 - Prob. 63ECh. 3.2 - (a) If g is differentiable, the Reciprocal Rule...Ch. 3.3 - Differentiate. f(x) = x2 sin xCh. 3.3 - Differentiate. f(x) = x cos x + 2 tan xCh. 3.3 - Differentiate. f(x) = ex cos xCh. 3.3 - Differentiate. y = 2 sec x csc xCh. 3.3 - Differentiate. y = sec tanCh. 3.3 - Differentiate. g() = e(tan )Ch. 3.3 - Differentiate. y = c cos t + t2 sin tCh. 3.3 - Differentiate. f(t)=cottetCh. 3.3 - Prob. 9ECh. 3.3 - Differentiate. y = sin cosCh. 3.3 - Differentiate f()=sin1+cosCh. 3.3 - Differentiate. y=cosx1sinxCh. 3.3 - Differentiate. y=tsint1+tCh. 3.3 - Differentiate. y=sint1+tantCh. 3.3 - Differentiate. f() = cos sinCh. 3.3 - Differentiate. f(t) = tet cot tCh. 3.3 - Prove that ddx(cscx)=cscxcotx.Ch. 3.3 - Prove that ddx(secx)=secxtanxCh. 3.3 - Prove that ddx(cotx)=csc2x.Ch. 3.3 - Prove, using the definition of derivative. that if...Ch. 3.3 - Find an equation of the tangent line to the curve...Ch. 3.3 - Find an equation of the tangent line to the curve...Ch. 3.3 - Find an equation of the tangent line to the curve...Ch. 3.3 - Find an equation of the tangent line to the curve...Ch. 3.3 - (a) Find an equation of the tangent line to the...Ch. 3.3 - Prob. 26ECh. 3.3 - (a) If f(x) = sec x x, find f'(x). (b) Check to...Ch. 3.3 - (a) If f(x) = ex cos x, find f'(x) and f"(x). (b)...Ch. 3.3 - If H() = sin , find H'() and H"( ).Ch. 3.3 - If f(t) = sec t, find f"(/4).Ch. 3.3 - (a) Use the Quotient Rule to differentiate the...Ch. 3.3 - Suppose f(/3) = 4 and f'(/3) = 2, and let g(x) =...Ch. 3.3 - For what values of x does the graph of f have a...Ch. 3.3 - For what values of x does the graph of f have a...Ch. 3.3 - A mass on a spring vibrates horizontally on a...Ch. 3.3 - An elastic band is hung on a hook and a mass is...Ch. 3.3 - A ladder 10 ft long rests against a vertical wall....Ch. 3.3 - An object with weight W is dragged along a...Ch. 3.3 - Find the limit. limx0sin5x3xCh. 3.3 - Find the limit. limx0sinxsinxCh. 3.3 - Find the limit. limt0tan6tsin2tCh. 3.3 - Prob. 42ECh. 3.3 - Find the limit. limx0sin3x5x34xCh. 3.3 - Find the limit. limx0sin3xsin5xx2Ch. 3.3 - Prob. 45ECh. 3.3 - Find the limit. limx0cscxsin(sinx)Ch. 3.3 - Prob. 47ECh. 3.3 - Find the limit. limx0sin(x2)xCh. 3.3 - Prob. 49ECh. 3.3 - Prob. 50ECh. 3.3 - Find the given derivative by finding the first few...Ch. 3.3 - Find the given derivative by finding the first few...Ch. 3.3 - Find constants A and B such that the function y =...Ch. 3.3 - (a) Evaluate limxxsin1x. (b) Evaluate limx0xsin1x....Ch. 3.3 - Differentiate each trigonometric identity to...Ch. 3.3 - A semicircle with diameter PQ sits on an isosceles...Ch. 3.3 - The figure shows a circular arc of length s and a...Ch. 3.3 - Prob. 58ECh. 3.4 - Write the composite function in the form f(g(x))....Ch. 3.4 - Write the composite function in the form f(g(x))....Ch. 3.4 - Write the composite function in the form f(g(x))....Ch. 3.4 - Write the composite function in the form f(g(x))....Ch. 3.4 - Write the composite function in the form f(g(x))....Ch. 3.4 - Write the composite function in the form f(g(x))....Ch. 3.4 - Find the derivative of the function. F(x) = (5x6 +...Ch. 3.4 - Find the derivative of the function. F (x) = (1 +...Ch. 3.4 - Find the derivative of the function. f(x)=5x+1Ch. 3.4 - Find the derivative of the function. f(x)=1x213Ch. 3.4 - Find the derivative of the function. f() = cos(2)Ch. 3.4 - Find the derivative of the function. g() = cos2Ch. 3.4 - Find the derivative of the function. y = x2e3xCh. 3.4 - Find the derivative of the function. f(t) = t sin ...Ch. 3.4 - Find the derivative of the function. f(t) = eat...Ch. 3.4 - Find the derivative of the function. g(x)=ex2xCh. 3.4 - Find the derivative of the function. f(x) = (2x ...Ch. 3.4 - Find the derivative of the function. g(x) = (x2 +...Ch. 3.4 - Find the derivative of the function. h(t) = (t +...Ch. 3.4 - Find the derivative of the function. F(t) = (3t ...Ch. 3.4 - Find the derivative of the function. y=xx+1Ch. 3.4 - Find the derivative of the function. y=(x+1x)5Ch. 3.4 - Find the derivative of the function. y = e tanCh. 3.4 - Find the derivative of the function. f(t)2t3Ch. 3.4 - Find the derivative of the function....Ch. 3.4 - Find the derivative of the function....Ch. 3.4 - Find the derivative of the function. r(t)=10t2Ch. 3.4 - Find the derivative of the function. f(z) =...Ch. 3.4 - Find the derivative of the function....Ch. 3.4 - Find the derivative of the function. J() = tan2(n)Ch. 3.4 - Find the derivative of the function. F(t) = et sin...Ch. 3.4 - Find the derivative of the function. F(t)=t2t3+1Ch. 3.4 - Find the derivative of the function. G(x) = 4C/xCh. 3.4 - Prob. 34ECh. 3.4 - Find the derivative of the function....Ch. 3.4 - Prob. 36ECh. 3.4 - Find the derivative of the function. y = cot2(sin...Ch. 3.4 - Prob. 38ECh. 3.4 - Find the derivative of the function. f(t) =...Ch. 3.4 - Find the derivative of the function. y = esin 2x +...Ch. 3.4 - Find the derivative of the function....Ch. 3.4 - Find the derivative of the function. y=x+x+xCh. 3.4 - Find the derivative of the function. g(x) = (2...Ch. 3.4 - Find the derivative of the function. y=234xCh. 3.4 - Find the derivative of the function....Ch. 3.4 - Find the derivative of the function. y = [x + (x +...Ch. 3.4 - Find y and y. y = cos(sin 3)Ch. 3.4 - Find y and y. y=1(1+tanx)2Ch. 3.4 - Find y and y. y=1sectCh. 3.4 - Find y and y. y=eexCh. 3.4 - Find an equation of the tangent line to the curve...Ch. 3.4 - Find an equation of the tangent line to the curve...Ch. 3.4 - Find an equation of the tangent line to the curve...Ch. 3.4 - Find an equation of the tangent line to the curve...Ch. 3.4 - Prob. 55ECh. 3.4 - (a) The curve y=|x|/2x2 is called a bullet-nose...Ch. 3.4 - (a) If f(x)=2x2x, find f(x). (b) Check to see that...Ch. 3.4 - Prob. 58ECh. 3.4 - Find all points on the graph of the function f(x)...Ch. 3.4 - At what point on the curve y=1+2x is the tangent...Ch. 3.4 - If F(x) = f(g(x)), where f(2) = 8, f(2) = 4, f(5)...Ch. 3.4 - If h(x)=4+3f(x), where f(1) = 7andf(1) = 4, find...Ch. 3.4 - A table of values for f, g, f, and g is given. (a)...Ch. 3.4 - Prob. 64ECh. 3.4 - If f and g are the functions whose graphs are...Ch. 3.4 - If f is the function whose graph is shown, let...Ch. 3.4 - If g(x)=f(x), where the graph off is shown,...Ch. 3.4 - Prob. 68ECh. 3.4 - Suppose f is differentiable on . Let F(x) = f(ex)...Ch. 3.4 - Let g(x) = ecx + f(x) and h(x) = ekxf(x), where...Ch. 3.4 - Let r(x) = f(g(h(x))), where h(1) = 2, g(2) = 3,...Ch. 3.4 - If g is a twice differentiable function and f(x) =...Ch. 3.4 - Prob. 73ECh. 3.4 - Prob. 74ECh. 3.4 - Show that the function y = e2x (A cos 3x + B sin...Ch. 3.4 - For what values of r does the function y = erx...Ch. 3.4 - Find the 50th derivative of y = cos 2x.Ch. 3.4 - Prob. 78ECh. 3.4 - The displacement of a particle on a vibrating...Ch. 3.4 - If the equation of motion of a particle is given...Ch. 3.4 - A Cepheid variable star is a star whose brightness...Ch. 3.4 - In Example 1.3.4 we arrived at a model for the...Ch. 3.4 - Prob. 83ECh. 3.4 - Under certain circumstance a rumor spreads...Ch. 3.4 - The average blood alcohol concentration (BAC) of...Ch. 3.4 - In Section 1.4 we modeled the world population...Ch. 3.4 - Prob. 87ECh. 3.4 - Air is being pumped into a spherical weather...Ch. 3.4 - Prob. 89ECh. 3.4 - Prob. 90ECh. 3.4 - Use the Chain Rule to prove the following. (a) The...Ch. 3.4 - Prob. 94ECh. 3.4 - (a) If n is a positive integer, prove that...Ch. 3.4 - Prob. 96ECh. 3.4 - Use the Chain Rule to show that if is measured in...Ch. 3.4 - (a) Write |x|=x2 and use the Chain Rule to show...Ch. 3.4 - Prob. 99ECh. 3.4 - Prob. 100ECh. 3.5 - (a) Find y by implicit differentiation. (b) Solve...Ch. 3.5 - (a) Find y by implicit differentiation. (b) Solve...Ch. 3.5 - (a) Find y by implicit differentiation. (b) Solve...Ch. 3.5 - (a) Find y by implicit differentiation. (b) Solve...Ch. 3.5 - Find dy/dx by implicit differentiation. 5. x2 4xy...Ch. 3.5 - Find dy/dx by implicit differentiation. 6. 2x2 +...Ch. 3.5 - Find dy/dx by implicit differentiation. 7. x4 +...Ch. 3.5 - Find dy/dx by implicit differentiation. 8. x3 xy2...Ch. 3.5 - Find dy/dx by implicit differentiation. 9....Ch. 3.5 - Find dy/dx by implicit differentiation. 10. xey =...Ch. 3.5 - Find dy/dx by implicit differentiation. 11. y cos...Ch. 3.5 - Find dy/dx by implicit differentiation. 12....Ch. 3.5 - Find dy/dx by implicit differentiation. 13....Ch. 3.5 - Find dy/dx by implicit differentiation. 14. ey sin...Ch. 3.5 - Find dy/dx by implicit differentiation. 15. ex/y...Ch. 3.5 - Find dy/dx by implicit differentiation. 16....Ch. 3.5 - Find dy/dx by implicit differentiation. 17....Ch. 3.5 - Find dy/dx by implicit differentiation. 18. x sin...Ch. 3.5 - Find dy/dx by implicit differentiation. 19....Ch. 3.5 - Find dy/dx by implicit differentiation. 20....Ch. 3.5 - If f(x) + x2 [f(x)]3 = 10 and f(1) = 2, find f(1).Ch. 3.5 - If g(x) + x sin g(x) = x2, find g(0).Ch. 3.5 - Regard y as the independent variable and x as the...Ch. 3.5 - Regard y as the independent variable and x as the...Ch. 3.5 - Use implicit differentiation to find an equation...Ch. 3.5 - Use implicit differentiation to find an equation...Ch. 3.5 - Use implicit differentiation to find an equation...Ch. 3.5 - Use implicit differentiation to find an equation...Ch. 3.5 - Use implicit differentiation to find an equation...Ch. 3.5 - Use implicit differentiation to find an equation...Ch. 3.5 - Use implicit differentiation to find an equation...Ch. 3.5 - Use implicit differentiation to find an equation...Ch. 3.5 - (a) The curve with equation y2 = 5x4 x2 is called...Ch. 3.5 - (a) The curve with equation y2 = x3 + 3x2 is...Ch. 3.5 - Find y by implicit differentiation. 35. x2 + 4y2 =...Ch. 3.5 - Find y by implicit differentiation. 36. x2 + xy +...Ch. 3.5 - Find y by implicit differentiation. 37. sin y +...Ch. 3.5 - Find y by implicit differentiation. 38. x3 y3 = 7Ch. 3.5 - If xy + ey = e, find the value of y at the point...Ch. 3.5 - If x2 + xy + y3 = 1, find the value of y at the...Ch. 3.5 - Find the points on the lemniscate in Exercise 31...Ch. 3.5 - Show by implicit differentiation that the tangent...Ch. 3.5 - Find an equation of the tangent line to the...Ch. 3.5 - Show that the sum of the x-and y-intercepts of any...Ch. 3.5 - Show, using implicit differentiation, that any...Ch. 3.5 - The Power Rule can be proved using implicit...Ch. 3.5 - Find the derivative of the function. Simplify...Ch. 3.5 - Find the derivative of the function. Simplify...Ch. 3.5 - Find the derivative of the function. Simplify...Ch. 3.5 - Prob. 52ECh. 3.5 - Find the derivative of the function. Simplify...Ch. 3.5 - Find the derivative of the function. Simplify...Ch. 3.5 - Find the derivative of the function. Simplify...Ch. 3.5 - Prob. 56ECh. 3.5 - Find the derivative of the function. Simplify...Ch. 3.5 - Find the derivative of the function. Simplify...Ch. 3.5 - Prob. 59ECh. 3.5 - Find the derivative of the function. Simplify...Ch. 3.5 - Find f(x). Check that your answer is reasonable by...Ch. 3.5 - Prob. 62ECh. 3.5 - Prove the formula for (d/dx)(cos1x) by the same...Ch. 3.5 - (a) One way of defining sec1x is to say that...Ch. 3.5 - Two curves are orthogonal if their tangent lines...Ch. 3.5 - Prob. 66ECh. 3.5 - Two curves are orthogonal if their tangent lines...Ch. 3.5 - Prob. 68ECh. 3.5 - Show that the ellipse x2/a2 + y2/b2 = 1 and the...Ch. 3.5 - Prob. 70ECh. 3.5 - (a) The van der Waals equation for n moles of a...Ch. 3.5 - The equation x2 xy + y2 = 3 re presents a...Ch. 3.5 - (a) Where does the normal line to the ellipse x2 ...Ch. 3.5 - Find all points on the curve x2y2 + xy = 2 where...Ch. 3.5 - Find equations of both the tangent lines to the...Ch. 3.5 - (a) Suppose f is a one-to-one differentiable...Ch. 3.5 - Prob. 78ECh. 3.5 - The Bessel function of order 0, y = J(x),...Ch. 3.5 - The figure shows a lamp located three units to the...Ch. 3.6 - Explain why the natural logarithmic function y =...Ch. 3.6 - Differentiate the function. f(x) = x ln x xCh. 3.6 - Differentiate the function. f(x ) = sin(ln x)Ch. 3.6 - Differentiate the function. f(x) = ln(sin2x)Ch. 3.6 - Differentiate the function. f(x)=ln1xCh. 3.6 - Differentiate the function. y=1lnxCh. 3.6 - Differentiate the function. f(x) = log10(1 + cos...Ch. 3.6 - Differentiate the function. f(x)log10xCh. 3.6 - Differentiate the function. g(x) = ln(xe2x)Ch. 3.6 - Differentiate the function. g(t)=1+lntCh. 3.6 - Differentiate the function. F(t) =(ln t)2 sin tCh. 3.6 - Differentiate the function. h(x)=ln(x+x21)Ch. 3.6 - Differentiate the function. G(y)=ln(2y+1)5y2+1Ch. 3.6 - Differentiate the function. p(v)=lnv1vCh. 3.6 - Differentiate the function. F(s) = ln ln sCh. 3.6 - Differentiate the function. y = ln |1 + t t3|Ch. 3.6 - Differentiate the function. T(z) = 2z log2zCh. 3.6 - Differentiate the function. y = ln(csc x cot x)Ch. 3.6 - Differentiate the function. y = ln(ex + xex)Ch. 3.6 - Differentiate the function. H(z)=a2z2a2+z2Ch. 3.6 - Differentiate the function. y = tan[ln(ax + b)]Ch. 3.6 - Differentiate the function. y = log2 (x log5 x)Ch. 3.6 - Find y and y. y=xlnxCh. 3.6 - Find y and y. y=lnx1+lnxCh. 3.6 - Find y and y. y = ln |sec x|Ch. 3.6 - Find y and y. y = ln(l + ln x)Ch. 3.6 - Differentiate f and find the domain of f....Ch. 3.6 - Differentiate f and find the domain of f....Ch. 3.6 - Differentiate f and find the domain of f. f(x) =...Ch. 3.6 - Differentiate f and find the domain of f. f(x) ln...Ch. 3.6 - If f(x) = ln(x + ln x), find f(1).Ch. 3.6 - If f(x) = cos(ln x2), find f(1).Ch. 3.6 - Find an equation of the tangent line to the curve...Ch. 3.6 - Find an equation of the tangent line to the curve...Ch. 3.6 - If f(x) = sin x + ln x, find f(x). Check that your...Ch. 3.6 - Find equations of the tangent lines to the curve y...Ch. 3.6 - Let f(x) = cx + ln(cos x). For what value of c is...Ch. 3.6 - Let f(x) = logb (3x2 2). For what value of b is...Ch. 3.6 - Use logarithmic differentiation to find the...Ch. 3.6 - Use logarithmic differentiation to find the...Ch. 3.6 - Use logarithmic differentiation to find the...Ch. 3.6 - Use logarithmic differentiation to find the...Ch. 3.6 - Use logarithmic differentiation to find the...Ch. 3.6 - Use logarithmic differentiation to find the...Ch. 3.6 - Use logarithmic differentiation to find the...Ch. 3.6 - Use logarithmic differentiation to find the...Ch. 3.6 - Use logarithmic differentiation to find the...Ch. 3.6 - Use logarithmic differentiation to find the...Ch. 3.6 - Use logarithmic differentiation to find the...Ch. 3.6 - Use logarithmic differentiation to find the...Ch. 3.6 - Find y if y = ln(x2 + y2).Ch. 3.6 - Find y if xy = yx.Ch. 3.6 - Find a formula for f(n)(x) if f(x) = ln(x 1).Ch. 3.6 - Find d9dx9(x8lnx).Ch. 3.6 - Use the definition of derivative to prove that...Ch. 3.6 - Show that limn(1+xn)n=exfor any x 0.Ch. 3.7 - A particle moves according to a law of motion s =...Ch. 3.7 - A particle moves according to a law of motion s =...Ch. 3.7 - A particle moves according to a law of motion s =...Ch. 3.7 - A particle moves according to a law of motion s =...Ch. 3.7 - Graphs of the velocity functions of two particles...Ch. 3.7 - Graphs of the position functions of two particles...Ch. 3.7 - The height (in meters) of a projectile shot...Ch. 3.7 - If a ball is thrown vertically upward with a...Ch. 3.7 - If a rock is thrown vertically upward from the...Ch. 3.7 - A particle moves with position function s = t4 ...Ch. 3.7 - (a) A company makes computer chips from square...Ch. 3.7 - (a) Sodium chlorate crystals are easy to grow in...Ch. 3.7 - (a) Find the average rate of change of the area of...Ch. 3.7 - A stone is dropped into a lake, creating a...Ch. 3.7 - A spherical balloon is being inflated. Find the...Ch. 3.7 - (a) The volume of a growing spherical cell is...Ch. 3.7 - The mass of the part of a metal rod that lies...Ch. 3.7 - If a tank holds 5000 gallons of water, which...Ch. 3.7 - The quantity of charge Q in coulombs (C) that has...Ch. 3.7 - Newtons Law of Gravitation says that the magnitude...Ch. 3.7 - Prob. 21ECh. 3.7 - Some of the highest tides in the world occur in...Ch. 3.7 - Boyles Law states that when a sample of gas is...Ch. 3.7 - If, in Example 4, one molecule of the product C is...Ch. 3.7 - In Example 6 we considered a bacteria population...Ch. 3.7 - The number of yeast cells in a laboratory culture...Ch. 3.7 - Prob. 28ECh. 3.7 - Prob. 29ECh. 3.7 - Prob. 30ECh. 3.7 - Prob. 31ECh. 3.7 - The cost function for a certain commodity is C(q)...Ch. 3.7 - Prob. 33ECh. 3.7 - If R denotes the reaction of the body to some...Ch. 3.7 - Patients undergo dialysis treatment to remove urea...Ch. 3.7 - Invasive species often display a wave of advance...Ch. 3.7 - The gas law for an ideal gas at absolute...Ch. 3.7 - In a fish farm, a population of fish is introduced...Ch. 3.7 - In the study of ecosystems, predator-prey models...Ch. 3.8 - A population of protozoa develops with a constant...Ch. 3.8 - A common inhabitant of human intestines is the...Ch. 3.8 - A bacteria culture initially contains 100 cells...Ch. 3.8 - A bacteria culture grows with constant relative...Ch. 3.8 - The table gives estimates of the world population,...Ch. 3.8 - The table gives the population of Indonesia, in...Ch. 3.8 - Experiments show that if the chemical reaction...Ch. 3.8 - Strontium-90 has a half-life of 28 days. (a) A...Ch. 3.8 - The half-life of cesium-137 is 30 years. Suppose...Ch. 3.8 - A sample oflritium-3 decayed to 94.5% of its...Ch. 3.8 - Scientists can determine the age of ancient...Ch. 3.8 - Dinosaur fossils are too old to be reliably dated...Ch. 3.8 - Prob. 13ECh. 3.8 - A curve passes through the point (0, 5) and has...Ch. 3.8 - A roast turkey is taken from an oven when its...Ch. 3.8 - In a murder investigation, the temperature of the...Ch. 3.8 - When a cold drink is taken from a refrigerator,...Ch. 3.8 - A freshly brewed cup of coffee has temperature 95C...Ch. 3.8 - Prob. 19ECh. 3.8 - (a) If 1000 is borrowed at 8% interest, find the...Ch. 3.8 - (a) If 3000 is invested at 5% interest, find the...Ch. 3.8 - (a) How long will it take an investment to double...Ch. 3.9 - Prob. 1ECh. 3.9 - (a) If A is the area of a circle with radius r and...Ch. 3.9 - Each side of a square is increasing at a rate of 6...Ch. 3.9 - The length of a rectangle is increasing at a rate...Ch. 3.9 - A cylindrical tank with radius 5 m is being filled...Ch. 3.9 - The radius of a sphere is increasing at a rate of...Ch. 3.9 - The radius of a spherical ball is increasing at a...Ch. 3.9 - The area of a triangle with sides of lengths a and...Ch. 3.9 - Suppose y=2x+1, where x and y are functions of t....Ch. 3.9 - Suppose 4x2 + 9y2 = 36, where x and y are...Ch. 3.9 - If x2 + y2 + z2 = 9, dx/dt = 5, and dy/dt = 4,...Ch. 3.9 - A particle is moving along a hyperbola xy = 8. As...Ch. 3.9 - (a) What quantities are given in the problem? (b)...Ch. 3.9 - (a) What quantities are given in the problem? (b)...Ch. 3.9 - (a) What quantities are given in the problem? (b)...Ch. 3.9 - (a) What quantities are given in the problem? (b)...Ch. 3.9 - Two cars start moving from the same point. One...Ch. 3.9 - A spotlight on the ground shines on a wall 12m...Ch. 3.9 - A man starts walking north at 4 ft/s from a point...Ch. 3.9 - A baseball diamond is a square with side 90 ft. A...Ch. 3.9 - The altitude of a triangle is increasing at a rate...Ch. 3.9 - A boat is pulled into a dock by a rope attached to...Ch. 3.9 - At noon, ship A is 100 km west of ship B. Ship A...Ch. 3.9 - Prob. 24ECh. 3.9 - Water is leaking out of an inverted conical tank...Ch. 3.9 - A trough is 10 ft long and its ends have the shape...Ch. 3.9 - A water trough is 10m long and a cross-section has...Ch. 3.9 - A swimming pool is 20 ft wide, 40 ft long, 3 ft...Ch. 3.9 - Gravel is being dumped from a conveyor belt at a...Ch. 3.9 - A kite 100ft above the ground moves horizontally...Ch. 3.9 - The sides of an equilateral triangle are...Ch. 3.9 - How fast is the angle between the ladder and the...Ch. 3.9 - The top of a ladder slides down a vertical wall at...Ch. 3.9 - According to the model we used to solve Example 2,...Ch. 3.9 - Prob. 35ECh. 3.9 - A faucet is filling a hemispherical basin of...Ch. 3.9 - Boyles Law states that when a sample of gas is...Ch. 3.9 - When air expands adiabatically (without gaining or...Ch. 3.9 - If two resistors with resistances R1 and R2 are...Ch. 3.9 - Brain weight B as a function of body weight Win...Ch. 3.9 - Two sides of a triangle have lengths 12 m and 15...Ch. 3.9 - Two carts, A and B, are connected by a rope 39 ft...Ch. 3.9 - A television camera is positioned 4000 ft from the...Ch. 3.9 - A lighthouse is located on a small island 3 km...Ch. 3.9 - A plane flies horizontally at an altitude of 5 km...Ch. 3.9 - A Ferris wheel with a radius of 10m is rotating at...Ch. 3.9 - A plane flying with a constant speed of 300 km/h...Ch. 3.9 - Two people start from the same point. One walks...Ch. 3.9 - A runner sprints around a circular track of radius...Ch. 3.9 - The minute hand on a watch is 8 mm long and the...Ch. 3.10 - Find the linearization L(x) of the function at n....Ch. 3.10 - Find the linearization L(x) of the function at n....Ch. 3.10 - Find the linearization L(x) of the function at n....Ch. 3.10 - Find the linearization L(x) of the function at n....Ch. 3.10 - Find the linear approximation of the function...Ch. 3.10 - Find the linear approximation of the function...Ch. 3.10 - Prob. 7ECh. 3.10 - Prob. 8ECh. 3.10 - Verify the given linear approximation at a = 0....Ch. 3.10 - Prob. 10ECh. 3.10 - Find the differential of each function. 11. (a) y...Ch. 3.10 - Find the differential of each function. 12. (a)...Ch. 3.10 - Find the differential of each function. 13. (a)...Ch. 3.10 - Find the differential of each function. 14. (a) y...Ch. 3.10 - (a) Find the differential dy and (b) evaluate dy...Ch. 3.10 - (a) Find the differential dy and (b) evaluate dy...Ch. 3.10 - (a) Find the differential dy and (b) evaluate dy...Ch. 3.10 - Prob. 18ECh. 3.10 - Compute y and dy for the given values of x and dx...Ch. 3.10 - Compute y and dy for the given values of x and dx...Ch. 3.10 - Compute y and dy for the given values of x and dx...Ch. 3.10 - Prob. 22ECh. 3.10 - Use a linear approximation (or differentials) to...Ch. 3.10 - Use a linear approximation (or differentials) to...Ch. 3.10 - Use a linear approximation (or differentials) to...Ch. 3.10 - Use a linear approximation (or differentials) to...Ch. 3.10 - Use a linear approximation (or differentials) to...Ch. 3.10 - Use a linear approximation (or differentials) to...Ch. 3.10 - Explain, in terms of linear approximations or...Ch. 3.10 - Explain, in terms of linear approximations or...Ch. 3.10 - Explain, in terms of linear approximations or...Ch. 3.10 - Prob. 32ECh. 3.10 - The edge of a cube was found to be 30 cm with a...Ch. 3.10 - The radius of a circular disk is given as 24 cm...Ch. 3.10 - The circumference of a sphere was measured to be...Ch. 3.10 - Use differentials to estimate the amount of paint...Ch. 3.10 - (a) Use differentials to find a formula for the...Ch. 3.10 - One side of a right triangle is known to be 20 cm...Ch. 3.10 - If a current I passes through a resistor with...Ch. 3.10 - When blood flows along a blood vessel, the flux F...Ch. 3.10 - Establish the following rules for working with...Ch. 3.10 - Prob. 42ECh. 3.10 - Suppose that the only information we have about a...Ch. 3.10 - Suppose that we dont have a formula for g(x) but...Ch. 3.11 - Find the numerical value of each expression. 1....Ch. 3.11 - Find the numerical value of each expression. 2....Ch. 3.11 - Find the numerical value of each expression. 3....Ch. 3.11 - Find the numerical value of each expression. 4....Ch. 3.11 - Find the numerical value of each expression. 5....Ch. 3.11 - Prob. 6ECh. 3.11 - Prove the identity. 7. sinh(x) = sinh x (This...Ch. 3.11 - Prob. 8ECh. 3.11 - Prove the identity. 9. cosh x + sinh x = exCh. 3.11 - Prove the identity. 10. cosh x sinh r = exCh. 3.11 - Prove the identity. 11. sinh(x + y) = sinh x cosh...Ch. 3.11 - Prob. 12ECh. 3.11 - Prove the identity. 13. coth2x 1 = csch2xCh. 3.11 - Prove the identity. 14....Ch. 3.11 - Prove the identity. 15. sinh 2x = 2 sinh x cosh xCh. 3.11 - Prob. 16ECh. 3.11 - Prove the identity. 17. tanh(lnx)=x21x2+1Ch. 3.11 - Prove the identity. 18. 1+tanhx1tanhx=e2xCh. 3.11 - Prove the identity. 19. (cosh x + sinh x)n = cosh...Ch. 3.11 - If x=1213 find the values of the other hyperbolic...Ch. 3.11 - If cosh=53 and x 0. find the values of the other...Ch. 3.11 - Prob. 22ECh. 3.11 - Use the definitions of the hyperbolic functions to...Ch. 3.11 - Prove the formulas given in Table 1 for the...Ch. 3.11 - Give an alternative solution 10 Example 3 by...Ch. 3.11 - Prob. 26ECh. 3.11 - Prove Equation 5 using (a) the method of Example 3...Ch. 3.11 - Prob. 28ECh. 3.11 - Prob. 29ECh. 3.11 - Find the derivative. Simplify where possible. 30....Ch. 3.11 - Find the derivative. Simplify where possible. 31....Ch. 3.11 - Find the derivative. Simplify where possible. 32....Ch. 3.11 - Find the derivative. Simplify where possible. 33....Ch. 3.11 - Prob. 34ECh. 3.11 - Find the derivative. Simplify where possible. 35....Ch. 3.11 - Find the derivative. Simplify where possible. 36....Ch. 3.11 - Find the derivative. Simplify where possible. 37....Ch. 3.11 - Prob. 38ECh. 3.11 - Find the derivative. Simplify where possible. 39....Ch. 3.11 - Prob. 40ECh. 3.11 - Find the derivative. Simplify where possible. 41....Ch. 3.11 - Find the derivative. Simplify where possible. 42....Ch. 3.11 - Find the derivative. Simplify where possible. 43....Ch. 3.11 - Prob. 44ECh. 3.11 - Prob. 45ECh. 3.11 - Prob. 46ECh. 3.11 - Prob. 47ECh. 3.11 - The Gateway Arch in St. Louis was designed by Eero...Ch. 3.11 - Prob. 49ECh. 3.11 - Prob. 50ECh. 3.11 - Prob. 51ECh. 3.11 - Prob. 52ECh. 3.11 - Prob. 53ECh. 3.11 - A model for the velocity of a falling object after...Ch. 3.11 - (a) Show that any function of the form y = A sinh...Ch. 3.11 - If x = ln( sec + tan ), show that sec = cosh x.Ch. 3.11 - At what point of the curve y = cosh x does the...Ch. 3.11 - Investigate the family of functions fn(x) = tanh...Ch. 3 - State each differentiation rule both in symbols...Ch. 3 - State the derivative of each function. (a) y = xn...Ch. 3 - (a) How is the number e defined? (b) Express e as...Ch. 3 - (a) Explain how implicit differentiation works....Ch. 3 - Give several examples of how the derivative can be...Ch. 3 - Prob. 6RCCCh. 3 - (a) Write an expression for the linearization of f...Ch. 3 - Determine whether the statement is true or false....Ch. 3 - Determine whether the statement is true or false....Ch. 3 - Determine whether the statement is true or false....Ch. 3 - Determine whether the statement is true or false....Ch. 3 - Determine whether the statement is true or false....Ch. 3 - Determine whether the statement is true or false....Ch. 3 - Determine whether the statement is true or false....Ch. 3 - Determine whether the statement is true or false....Ch. 3 - Determine whether the statement is true or false....Ch. 3 - Prob. 10RQCh. 3 - Prob. 11RQCh. 3 - Determine whether the statement is true or false....Ch. 3 - Determine whether the statement is true or false....Ch. 3 - Determine whether the statement is true or false....Ch. 3 - Prob. 15RQCh. 3 - Calculate y'. 1. y = (x2 + x3)4Ch. 3 - Calculate y'. 2. y=1x1x35Ch. 3 - Prob. 3RECh. 3 - Calculate y'. 4. y=tanx1+cosxCh. 3 - Prob. 5RECh. 3 - Prob. 6RECh. 3 - Prob. 7RECh. 3 - Calculate y'. 8. xey = y sin xCh. 3 - Calculate y'. 9. y = ln(x ln x)Ch. 3 - Prob. 10RECh. 3 - Prob. 11RECh. 3 - Calculate y'. 12. y = (arcsin 2x)2Ch. 3 - Prob. 13RECh. 3 - Calculate y'. 14. y = ln sec xCh. 3 - Prob. 15RECh. 3 - Prob. 16RECh. 3 - Calculate y'. 17. y=arctanCh. 3 - Prob. 18RECh. 3 - Prob. 19RECh. 3 - Prob. 20RECh. 3 - Calculate y'. 21. y = 3x ln xCh. 3 - Prob. 22RECh. 3 - Prob. 23RECh. 3 - Calculate y'. 24. y=1/x+x3Ch. 3 - Prob. 25RECh. 3 - Prob. 26RECh. 3 - Prob. 27RECh. 3 - Prob. 28RECh. 3 - Calculate y'. 29. y=lnsinx12sin2xCh. 3 - Prob. 30RECh. 3 - Prob. 31RECh. 3 - Prob. 32RECh. 3 - Calculate y'. 33. y = ln | sec 5x + tan 5x |Ch. 3 - Prob. 34RECh. 3 - Calculate y'. 35. y = cot(3x2 + 5)Ch. 3 - Prob. 36RECh. 3 - Prob. 37RECh. 3 - Prob. 38RECh. 3 - Prob. 39RECh. 3 - Prob. 40RECh. 3 - Prob. 41RECh. 3 - Prob. 42RECh. 3 - Prob. 43RECh. 3 - Prob. 44RECh. 3 - Calculate y'. 45. y = ln( cosh 3x)Ch. 3 - Prob. 46RECh. 3 - Prob. 47RECh. 3 - Prob. 48RECh. 3 - Prob. 49RECh. 3 - Prob. 50RECh. 3 - Prob. 51RECh. 3 - Prob. 52RECh. 3 - Find y if x6 + y6 = 1.Ch. 3 - Find f(n)(x) if f(x) = 1/(2 x).Ch. 3 - Prob. 55RECh. 3 - Prob. 56RECh. 3 - Find an equation of the tangent to the curve at...Ch. 3 - Prob. 58RECh. 3 - Prob. 59RECh. 3 - Find equations of the tangent line and normal line...Ch. 3 - Find equations of the tangent line and normal line...Ch. 3 - If f(x) = xesin x find f(x). Graph f and f on the...Ch. 3 - Prob. 63RECh. 3 - (a) If f(x) = 4x tan x, /2 x /2, find f and f....Ch. 3 - At what points on the curve y = sin x + cos x, 0 ...Ch. 3 - Prob. 66RECh. 3 - Prob. 67RECh. 3 - Prob. 68RECh. 3 - Suppose that f(1) = 2 f(1) = 3 f(2) = 1 f'(2) = 2...Ch. 3 - If f and g are the functions whose graphs are...Ch. 3 - Find f in terms of g. f(x) = x2g(x)Ch. 3 - Prob. 72RECh. 3 - Find f in terms of g. f(x) = [g(x)]2Ch. 3 - Prob. 74RECh. 3 - Find f in terms of g. f(x) = g(ex)Ch. 3 - Prob. 76RECh. 3 - Prob. 77RECh. 3 - Find f in terms of g. f(x) = g(ln x)Ch. 3 - Prob. 79RECh. 3 - Prob. 80RECh. 3 - Find f in terms of f and g. h(x) = f(g(sin 4x))Ch. 3 - Prob. 82RECh. 3 - At what point on the curve y = [ln(x + 4)]2 is the...Ch. 3 - (a) Find an equation of the tangent to the curve y...Ch. 3 - Prob. 85RECh. 3 - The function C(t) = K(eat ebt), where a, b, and K...Ch. 3 - Prob. 87RECh. 3 - Prob. 88RECh. 3 - A particle moves on a vertical line so that its...Ch. 3 - Prob. 90RECh. 3 - Prob. 91RECh. 3 - Prob. 92RECh. 3 - A bacteria culture contains 200 cells initially...Ch. 3 - Cobalt-60 has a half-life of 5.24 years. (a) Find...Ch. 3 - Let C(t) be the concentration of a drug in the...Ch. 3 - A cup of hot chocolate has temperature 80C in a...Ch. 3 - Prob. 97RECh. 3 - A paper cup has the shape of a cone with height 10...Ch. 3 - A balloon is rising at a constant speed of 5 ft/s....Ch. 3 - Prob. 100RECh. 3 - Prob. 101RECh. 3 - (a) Find the linear approximation to f(x)=25x2...Ch. 3 - (a) Find the linearization of f(x)1+3x3 at a = 0....Ch. 3 - Prob. 104RECh. 3 - A window has the shape of a square surmounted by a...Ch. 3 - Prob. 106RECh. 3 - Prob. 107RECh. 3 - Express the limit as a derivative and evaluate....Ch. 3 - Prob. 109RECh. 3 - Suppose f is a differentiable function such that...Ch. 3 - Prob. 111RECh. 3 - Show that the length of the portion of any tangent...Ch. 3 - Find points P and Q on the parabola y = 1 x2 so...Ch. 3 - Prob. 2PCh. 3 - Prob. 3PCh. 3 - Prob. 4PCh. 3 - If f(x)=limtxsectsecxtx, find the value of f'(/4).Ch. 3 - Find the values of the constants a and b such that...Ch. 3 - Show that sin-1(tanh x) = tan1(sinh x).Ch. 3 - Prob. 8PCh. 3 - Prove that dndxn(sin4x+cos4x)=4n1cos(4x+n/2).Ch. 3 - Prob. 10PCh. 3 - Prob. 11PCh. 3 - Find all values of r such that the parabolas y =...Ch. 3 - How many lines are tangent to both of the circles...Ch. 3 - Prob. 14PCh. 3 - The figure shows a rotating wheel with radius 40...Ch. 3 - Tangent lines T1, and T2, are drawn at two points...Ch. 3 - Prob. 17PCh. 3 - Prob. 18PCh. 3 - Prob. 19PCh. 3 - Prob. 20PCh. 3 - (a) Use the identity for tan(x y) (see Equation...Ch. 3 - Prob. 22PCh. 3 - Prob. 23PCh. 3 - Prob. 24PCh. 3 - Prob. 25PCh. 3 - For what value of k does the equation e2x=kx have...Ch. 3 - Prob. 28PCh. 3 - If y=xa212a21arctansinxa+a21+cosx show that...Ch. 3 - Given an ellipse x2/a2 + y2/b2 = 1, where a b,...Ch. 3 - Find the two points on the curve y = x4 2x2 x...Ch. 3 - Suppose that three points on the parabola y = x2...Ch. 3 - Prob. 33PCh. 3 - Prob. 34PCh. 3 - Prob. 35P
Knowledge Booster
Learn more about
Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, calculus and related others by exploring similar questions and additional content below.Similar questions
- 5-6 Yes or No? If No, give a reason aIs the average rate of change of a function between x=a and x=b the slope of the secant line through (a,f(a)) and (b,f(b))?arrow_forwardChange in Direction A graph of directed distance switches from increasing to decreasing. What happens to velocity?arrow_forward
Recommended textbooks for you
- Algebra & Trigonometry with Analytic GeometryAlgebraISBN:9781133382119Author:SwokowskiPublisher:Cengage
 Algebra and Trigonometry (MindTap Course List)AlgebraISBN:9781305071742Author:James Stewart, Lothar Redlin, Saleem WatsonPublisher:Cengage Learning
Algebra and Trigonometry (MindTap Course List)AlgebraISBN:9781305071742Author:James Stewart, Lothar Redlin, Saleem WatsonPublisher:Cengage Learning Functions and Change: A Modeling Approach to Coll...AlgebraISBN:9781337111348Author:Bruce Crauder, Benny Evans, Alan NoellPublisher:Cengage Learning
Functions and Change: A Modeling Approach to Coll...AlgebraISBN:9781337111348Author:Bruce Crauder, Benny Evans, Alan NoellPublisher:Cengage Learning  College AlgebraAlgebraISBN:9781305115545Author:James Stewart, Lothar Redlin, Saleem WatsonPublisher:Cengage Learning
College AlgebraAlgebraISBN:9781305115545Author:James Stewart, Lothar Redlin, Saleem WatsonPublisher:Cengage Learning

Algebra & Trigonometry with Analytic Geometry
Algebra
ISBN:9781133382119
Author:Swokowski
Publisher:Cengage

Algebra and Trigonometry (MindTap Course List)
Algebra
ISBN:9781305071742
Author:James Stewart, Lothar Redlin, Saleem Watson
Publisher:Cengage Learning

Functions and Change: A Modeling Approach to Coll...
Algebra
ISBN:9781337111348
Author:Bruce Crauder, Benny Evans, Alan Noell
Publisher:Cengage Learning

College Algebra
Algebra
ISBN:9781305115545
Author:James Stewart, Lothar Redlin, Saleem Watson
Publisher:Cengage Learning
Finding Local Maxima and Minima by Differentiation; Author: Professor Dave Explains;https://www.youtube.com/watch?v=pvLj1s7SOtk;License: Standard YouTube License, CC-BY