
Concept explainers
The reaction force equation at point
The reaction force equation at point
The shear force equation for section
The shear force equation for section
The bending moment equation for section
The bending moment equation for section
The deflection equations for section
The deflection equations for section
Answer to Problem 18P
The reaction force equation at point
The reaction force equation at point
The shear force equation for section
The shear force equation for section
The bending moment equation for section
The bending moment equation for section
The deflection equations for section
The deflection equations for section
Explanation of Solution
Write the balanced force equation in vertical direction.
Here, the reaction at point
Take the net moment about point
Thus, the reaction force at point A is
Substitute
Thus, the reaction force at point
Take a section at a distance
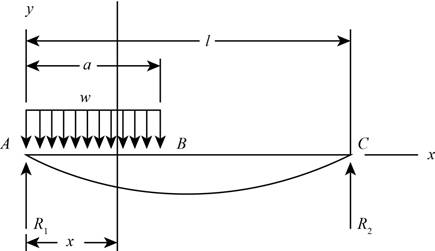
Figure (1)
Write the shear force equation for part AB.
Here, the shear force for the section
Substitute
Thus, the shear force equation for region
Take a section at a distance
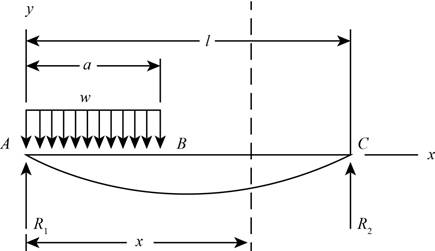
Figure (2)
Write the shear force equation for part
Here, the shear force for the section
Substitute
Thus, the shear force equation for region
Write the moment equation for section
Here, the moment for the section
Substitute
Thus, the bending moment equation for region AB is
Write the moment equation for section
Here, the moment for the section
Substitute
Thus, the bending moment equation for region
Write the bending moment equation for section
Here, Young’s modulus of the beam is
Substitute
Integrate Equation (VI).
Here, the integration constant is
Integrate Equation (VII).
Here, the second integration constant is
Substitute
Substitute
Here, the deflection for the section
Substitute
Thus, the beam deflection equation for region AB is
Write the bending moment equation for section
Here, the moment for the section
Substitute
Integrate the Equation (X).
Here, the first integration constant is
Integrate the Equation (XI).
Here, the second integration constant is
Substitute
Substitute
At
Equate the right hand side of equation (XI) and (XIII) and substitute
At
Substitute
Substitute
Substitute
Substitute
Solve the equation further,
Substitute
Thus, the beam deflection equation for region BC is
Want to see more full solutions like this?
Chapter 4 Solutions
Shigley's Mechanical Engineering Design (McGraw-Hill Series in Mechanical Engineering)
- Repeat Problem 2.5-9 for the flat bar shown in the figure but assume that and thatarrow_forward-4-4 A cantilever beam is supported at B by cable BC. The beam carries a uniform load q = 200 N/M. If the length of the beam is L = 3 m, find the force in the cable and the reactions at A. Ignore the axial flexibility of the cable.arrow_forwardA T-frame structure is torn posed of a prismatic beam ABC and a nonprismatic column DBF. The beam and the column have a pin support at .A and D, respectively. Both members are connected with a pin at B. The lengths and properties of the members are shown in the figure. Find the vertical displacement of the column at points F and B. Plot axial force (AFD) and axial displacement (ADD) diagrams For column DBF.arrow_forward
- Repeat Problem 9,5-15 for the anti-symmetric loading shown in the figure.arrow_forwardRepeat Problem 10.4-41 for the loading shown in the figure.arrow_forwardA bumper for a mine car is constructed with a spring of stiffness k = 1120 lb/in. (see figure). If a car weighing 3450 lb is traveling at velocity v = 7 mph when it strikes the spring, what is the maximum shortening of the spring?arrow_forward
- A heavy flywheel rotating at n revolutions per minute is rigidly attached to the end of a shaft of diameter d (see figure). If the bearing at A suddenly freezes, what will be the maximum angle of twist <£of the shaft? What is the corresponding maximum shear stress in the shaft? (Let L = length of the shaft, G = shear modulus of elasticity, and / = mass moment of inertia of the flywheel about the axis of the shaft. Also, disregard friction in the bearings at Sand Cand disregard the mass of the shaft.) Hint: Equate the kinetic energy of the rotating flywheel to the strain energy of the shaft.arrow_forwardAt a full d raw, an archer applies a pull of 130 N to the bowstring of the bow shown in the figure. Determine the bending moment at the midpoint of the bow.arrow_forwardRepeat Problem 11.3-9. Use two C 150 × 12.2 steel shapes and assume that E = 205 GPa and L = 6 m.arrow_forward
- Repeat Problem 6.4-14 but use the configuration of channel shapes and loading shown in the figure. Use P = 250 N.arrow_forwardRepeat Problem 6.2-1 but now assume that the steel plate is smaller (0.5 in. × 5 in.) and is aligned with the top of the beam as shown in the figure.arrow_forwardThe L-shaped arm ABCD shown in the figure lies in a vertical plane and pivots about a horizontal pin at A. The arm has a constant cross-sectional area and total weight W. A vertical spring of stiffness k supports the arm at point B. (a) Obtain a formula for the elongation of the spring due to the weight of the arm. (b) Repeat part (a) if the pin support at A is moved to D.arrow_forward
 Mechanics of Materials (MindTap Course List)Mechanical EngineeringISBN:9781337093347Author:Barry J. Goodno, James M. GerePublisher:Cengage Learning
Mechanics of Materials (MindTap Course List)Mechanical EngineeringISBN:9781337093347Author:Barry J. Goodno, James M. GerePublisher:Cengage Learning
