
Concept explainers
The infrared spectrum for methanol. CH3OH, is illustrated below. It shows the amount of light in the infrared region that methanol transmits as a function of wavelength. The vertical axis is the amount of light transmitted. At points near the top of the graph, most of the incident light is being transmitted by the sample (or, conversely, little light is absorbed). Therefore, the ″peaks″ or ″bands″ that descend from the top indicate light absorbed; the longer the band, the more light is being absorbed. The horizontal scale is in units of ″wavenumbers,″ abbreviated cm−1. The energy of light is given by Planck′s law as E = hc/λ; that is, E is proportional to 1/λ. Therefore, the horizontal scale is in units of 1/λ and reflects the energy of the light incident on the sample.
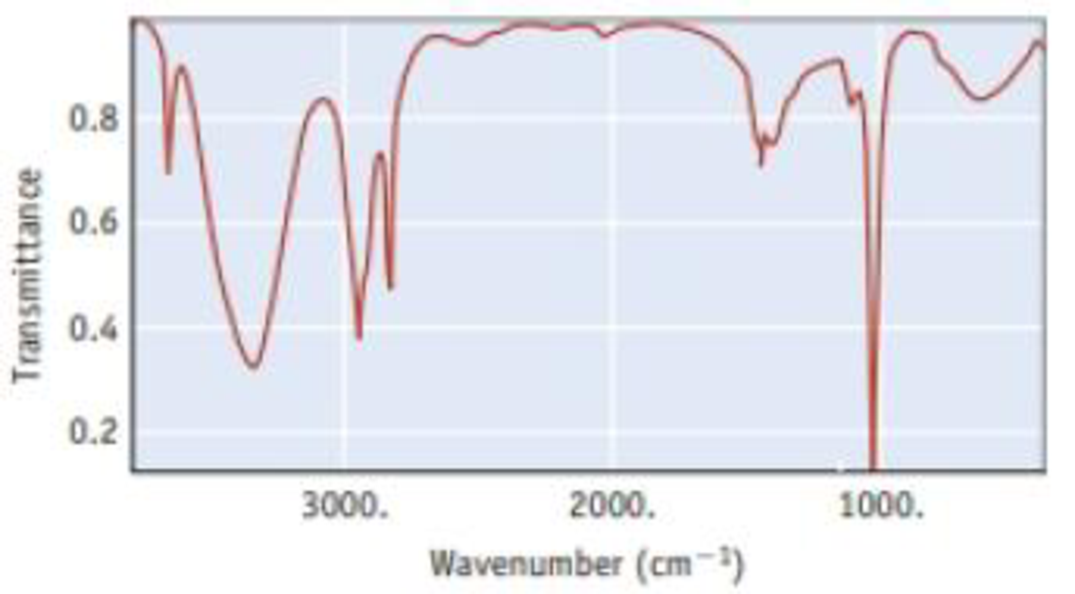
- (a) One point on the horizontal axis is marked as 2000 cm−1. What is the
wavelength of light at this point? - (b) Which is the low energy end of this spectrum (left or right), and which is the high energy end?
- (c) The broad absorption at about 3300-3400 cm−1 indicates that infrared radiation is interacting with the OH group of the methanol molecule. The narrower absorptions around 2800-3000 cm−1 are for interactions with C—H bonds. Which interaction requires more energy, with O—H or with C—H?
Trending nowThis is a popular solution!

Chapter 6 Solutions
Chemistry & Chemical Reactivity
- Ozone in the stratosphere absorbs ultraviolet light of wavelengths shorter than 320 nm, thus filtering out the most energetic radiation from sunlight. During this absorption, an ozone molecule absorbs a photon, which breaks an oxygen-oxygen bond, yielding an oxygen molecule and an oxygen atom: O3(g)+hvO2(g)+O(g) (Here, hv denotes a photon.) Suppose a flask of ozone is irradiated with a pulse of UV light of wavelength 275 nm. Assuming that each photon of this pulse that is absorbed breaks up one ozone molecule, calculate the energy absorbed per mole of O2 produced, giving the answer in kJ/mol.arrow_forwardTraffic signals are often now made of LEDs (light-emitting diodes). Amber and green ones are pictured here. (a) The light from an amber signal has a wave-length of 595 nm, and that from a green signal has a wavelength of 500 nm. Which has the higher frequency? (b) Calculate the frequency of amber light.arrow_forwardAn FM radio station found at 103.1 on the FM dial broadcasts at a frequency of 1.031188s1 (103.1 MHz). What is the wavelength of these radio waves in meters?arrow_forward
- The light produced by a red neon sign is due to the emission of light by excited neon atoms. Qualitatively describe the spectrum produced by passing light from a neon lamp through a prism.arrow_forward(a) Which color in the visible spectrum has the highest frequency? Which has the lowest frequency? (b) Is the wavelength of the radiation used in a microwave oven (2.45 GHz) longer or shorter than that from your favorite FM radio station (for example, 91.7 MHz)? (c) Are the wavelengths of x-rays longer or shorter than those of ultraviolet light? (d) Calculate the frequency of green light with a wavelength of 510. nm.arrow_forwardWhen a tube containing hydrogen atoms is energized by passing several thousand volts of electricity into the tube, the hydrogen emits light than when passed through a prism, resolves into the "bright line" spectrum shown in Fig. 11.10. Why do hydrogen atoms emit bright lines of specific wavelengths rather than a continuous spectrum?arrow_forward
- Photons of infrared radiation are responsible for much of the warmth we feel when holding our hands before a fire. These photons will also warm other objects. How many infrared photons with a wavelength of 1.5106 m must be absorbed by the water to warm a cup of water (175 g) from 25.0 C to 40 C?arrow_forwardRGB color television and computer displays use cathode ray tubes that produce colors by mixing red, green, and blue light. If we look at the screen with a magnifying glass, we can see individual dots turn on and off as the colors change. Using a spectrum of visible light, determine the approximate wavelength of each of these colors. What is the frequency and energy of a photon of each of these colors?arrow_forward6.103 Atomic absorption spectroscopy is based on the atomic spectra of the elements being studied. It can be used to determine the impurities in a metal sample. If an element is present, light at the appropriate wavelength is absorbed. You are working with a metal stamping company and the rolled steel you use to form panels for automobile doors is failing at an alarming rate. There is some chance that the problem is unacceptably high levels of manganese in the steel. Given that the atomic spectrum of manganese has three lines near 403 nm, how could you use a spectrometer to determine the amount of manganese in the steel?arrow_forward
 Chemistry & Chemical ReactivityChemistryISBN:9781133949640Author:John C. Kotz, Paul M. Treichel, John Townsend, David TreichelPublisher:Cengage Learning
Chemistry & Chemical ReactivityChemistryISBN:9781133949640Author:John C. Kotz, Paul M. Treichel, John Townsend, David TreichelPublisher:Cengage Learning Chemistry & Chemical ReactivityChemistryISBN:9781337399074Author:John C. Kotz, Paul M. Treichel, John Townsend, David TreichelPublisher:Cengage Learning
Chemistry & Chemical ReactivityChemistryISBN:9781337399074Author:John C. Kotz, Paul M. Treichel, John Townsend, David TreichelPublisher:Cengage Learning General Chemistry - Standalone book (MindTap Cour...ChemistryISBN:9781305580343Author:Steven D. Gammon, Ebbing, Darrell Ebbing, Steven D., Darrell; Gammon, Darrell Ebbing; Steven D. Gammon, Darrell D.; Gammon, Ebbing; Steven D. Gammon; DarrellPublisher:Cengage Learning
General Chemistry - Standalone book (MindTap Cour...ChemistryISBN:9781305580343Author:Steven D. Gammon, Ebbing, Darrell Ebbing, Steven D., Darrell; Gammon, Darrell Ebbing; Steven D. Gammon, Darrell D.; Gammon, Ebbing; Steven D. Gammon; DarrellPublisher:Cengage Learning Chemistry for Engineering StudentsChemistryISBN:9781337398909Author:Lawrence S. Brown, Tom HolmePublisher:Cengage Learning
Chemistry for Engineering StudentsChemistryISBN:9781337398909Author:Lawrence S. Brown, Tom HolmePublisher:Cengage Learning
 Principles of Modern ChemistryChemistryISBN:9781305079113Author:David W. Oxtoby, H. Pat Gillis, Laurie J. ButlerPublisher:Cengage Learning
Principles of Modern ChemistryChemistryISBN:9781305079113Author:David W. Oxtoby, H. Pat Gillis, Laurie J. ButlerPublisher:Cengage Learning





