
Concept explainers
The basic
Where
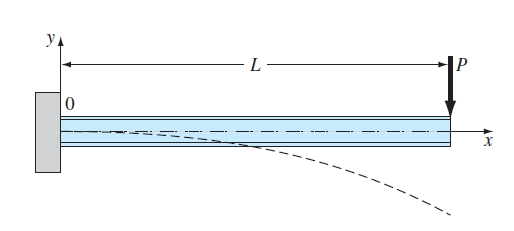
FIGURE P28.26
Want to see the full answer?
Check out a sample textbook solution
Chapter 28 Solutions
EBK NUMERICAL METHODS FOR ENGINEERS
- A Cantilever beam deflects downwards when a mass is attached to its free end. The deflection (8) is the function of beam stiffness(K), applied mass(M) and gravitational force(g=9.81 m/s2): K8=Mg Determine the stiffness of beam? The various mass are placed on the end of the beam and corresponding deflections are noted as follow: 150.05 200.05 Mass Deflection 0 0 50.15 99.90 0.6 1.8 3.0 3.6 using the "Correlation Coefficient" equation, check whether the 'line-fitting' has; (i) strong positive linear relationship (ii) strong negative linear relationship (iii) no linear relationship 250.20 299.95 350.05 401.00 4.8 6.0 6.2 7.5arrow_forwardStress, a (MPa) Strain, e (x10* m/m) Yong Modulus, E (GPa) 3.963 40.0 99.1 7.926 75.0 106 11.89 105.0 113.2 1.85 122.0 130.0 19.81 144,0 137.6 Table 2 Stress and Strain 3|Page Dissections 1. Draw the graph of stress against strain 2. Discusses the obtained results 3. From the graph find. stress ? Yong Modulus, E? 4. Why Compression test is important in industry ?arrow_forward100 80 60 40 20 0.002 0.004 0.006 0.008 0.01 0.012 Strain, in/in. FIGURE P1.17 1.18 Use Problem 1.17 to graphically determine the following: a. Modulus of resilience b. Toughness Hint: The toughness (u) can be determined by calculating the area under the stress-strain curve u = de where & is the strain at fracture. The preceding integral can be approxi- mated numerically by using a trapezoidal integration technique: u, = Eu, = o, + o e, - 6) %3D c. If the specimen is loaded to 40 ksi only and the lateral strain was found to be -0.00057 in./in., what is Poisson's ratio of this metal? d. If the specimen is loaded to 70 ksi only and then unloaded, what is the permanent strain? Stress, ksiarrow_forward
- A long steel rod is placed horizontally between two supports, one at each end. The rod bends a little in the center. Which property of this rod can be used to estimate how much the rod should bend at the center? 1. Its Shear Modulus 2. Its Young's Modulus 3. All of these Moduli can be used to compute how much it bends. 4. Its Bulk Modulus.arrow_forwardH WebAssign - ENGR 2331 Su2 x A 23 Changes in Lengths unde x yL.Het/web/Student/Assignment-Responses/last?dep326956848#Q3 : Apps M Gmail YouTube O Maps DETAILS UUMECHMATI Z.3.UT7. MT NOTES ASK TOUK TEACHEK A flat bar of rectangular cross section, length L, and constant thickness t is subjected to tension by forces P (see figure). b2 P b1 The width of the bar varies linearly from b, at the smaller end to b, at the larger end. Assume that the angle of taper is small. (a) Derive the following formula for the elongation of the bar. (Submit a file with a maximum size of 1 MB.) PL Et(b, - Choose File No file chosen This answer has not been graded yet. (b) Calculate the elongation (in inches), assuming L = 3 ft, t = 1.0 in., P = 23 kips, b, = 4.0 in., b, = 5.4 in., and E = 30 x 106 psi. (Use the deformation sign convention.) in. 73°F Partly sunny Watch it Need Help2 Read It O Type here to search hparrow_forwardA rectangular tube of outer width w = 7.5 m, outer height h = 5 m and thickness t = 0.17 m experiences bending through the x axis. What is the moment of inertia of the cross-sectional area In? y -- X MATLAB input variables: format shortEng W = 7.5; h = 5; t = 0.17; moment of inertia I, = m4arrow_forward
- 22°F Clear 1MMBU BU ► ► ► 20°HD®°°*EqqaHÛDin × ODE DDE DE DE File C:/Users/ignor/Downloads/Assignment%203%20(2).pdf T❘ Read aloud Ask Copilot Draw a) Use Newton's second law b) Use the Torque equation /// Collar A is free to slide with negligible friction on the circular guide mounted in a vertical frame. Find the EOM of collar A if the frame is given a velocity v and a constant horizontal acceleration a to the right. Search 1 A www of 6 TTTT | CD a laaa 8 o + ENG 60 T N 7:35 PM 1/17/2024 xarrow_forwardQ11. By using the Young's Modulus – Strength material selection chart in Figure Q11. Sketch the specific region which the strength, o is greater than 30 MPa and materials performance index, M = is less than 100. Submit Figure Q11. Earrow_forward(b) A design uses E > 100 GPa and M = oʻ/E > 100 MPA²/GPa. You are required to analyse and select the suitable materials using the Young Modulus (E) – Strength () materials selection chart in Figure Q12(b). Submit Figure Q12(b).arrow_forward
- For the spring-mass system shown below, If k = 7 KN/m and K2 = 8 KN/m, what is the overall stiffness of the system? elll elle k, k, Equivalent Spring Stiffness: Springs in Parallel: kEg = k1 + k2 + k3 + kn %3D Springs in Series: kn keq ka Answer: s page online.gmit.ie/mod/quiz/attempt.php?attempt%3D167036&cmid%3D155306&page%3D1... Type here to search Σarrow_forward3G 9:.. %79 Final 1st attem... F2 У - ахis Fs F4 F1 х - ахis X- axis y - axis F3 F2 F1 Figure (1) Figure (2) 250 N 36.87 D F2 60° 0.5 m 1 m o! 0.2 m 1 m 300 NE F1 1 m Figure (3) Figure (4) Q1] Answer the following questions: For figure (1): The object is subjected to two forces F1 = 25 N, and F2 = 50 N. Set x = 30°, 0 = 45° , and ß = 30°. 1- What is the magnitude of the resultant of these two forces? a) 39.4 N b) 80.1N c) 41.6 N d) 69.8 N e) 71.4 N f) 46.1 N g) None of them 2 - What is the direction of the resultant force measured counterclockwise from the positive x-axis? а) 14.30 b) 392.6° c) 9.2° d) 322.9° e) 6.8° f) 344.2° g) None of them For figure (2): The arm in is subjected to five forces as follows: F1 = 135 N, F2 = 98 N, F3 = 210 N, F4 = 56 N. If the y – direction resultant force is 144 N, and x = 40°, 0 = 50°, B = 70°: 3 – What is the magnitude of the force F5? a) 318.4 N b) 99.1N c) 151.6 N d) 36.5 N e) 111.2 N f) 18.8 N g) None of them 4 - What is the magnitude of the…arrow_forwardThe following related values of the pressure p in kN/m2 and the volume V in cubic meter where measured from the compression curve of an internal combustion engine indicator diagram. Assuming that P and V are connected by the law PVn: C, find the value of n. p 3450 2350 1725 680 270 130 V .0085 .0113 .0142 .0283 .0566 .0991arrow_forward
 Elements Of ElectromagneticsMechanical EngineeringISBN:9780190698614Author:Sadiku, Matthew N. O.Publisher:Oxford University Press
Elements Of ElectromagneticsMechanical EngineeringISBN:9780190698614Author:Sadiku, Matthew N. O.Publisher:Oxford University Press Mechanics of Materials (10th Edition)Mechanical EngineeringISBN:9780134319650Author:Russell C. HibbelerPublisher:PEARSON
Mechanics of Materials (10th Edition)Mechanical EngineeringISBN:9780134319650Author:Russell C. HibbelerPublisher:PEARSON Thermodynamics: An Engineering ApproachMechanical EngineeringISBN:9781259822674Author:Yunus A. Cengel Dr., Michael A. BolesPublisher:McGraw-Hill Education
Thermodynamics: An Engineering ApproachMechanical EngineeringISBN:9781259822674Author:Yunus A. Cengel Dr., Michael A. BolesPublisher:McGraw-Hill Education Control Systems EngineeringMechanical EngineeringISBN:9781118170519Author:Norman S. NisePublisher:WILEY
Control Systems EngineeringMechanical EngineeringISBN:9781118170519Author:Norman S. NisePublisher:WILEY Mechanics of Materials (MindTap Course List)Mechanical EngineeringISBN:9781337093347Author:Barry J. Goodno, James M. GerePublisher:Cengage Learning
Mechanics of Materials (MindTap Course List)Mechanical EngineeringISBN:9781337093347Author:Barry J. Goodno, James M. GerePublisher:Cengage Learning Engineering Mechanics: StaticsMechanical EngineeringISBN:9781118807330Author:James L. Meriam, L. G. Kraige, J. N. BoltonPublisher:WILEY
Engineering Mechanics: StaticsMechanical EngineeringISBN:9781118807330Author:James L. Meriam, L. G. Kraige, J. N. BoltonPublisher:WILEY





