
Concept explainers
The deflection of the shaft at point
The slope of the shaft at point
Answer to Problem 27P
The deflection of the shaft at point
The slope of the shaft at point
Explanation of Solution
Write the expression for the moment of inertia of the shaft.
Here, the diameter of the shaft is
Draw the free body diagram of the beam.
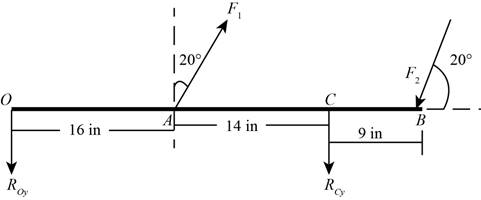
Figure (1)
The free body diagram of the beam in the direction of y-axis is shown figure (1).
Write the deflection equation along y-axis for beam 6 and beam 10 using Table A-9.
Here, the force component at point A along y-axis is
Write the force component at point
Here, the force component at
Write the force component at point
Here, the force component at
The free body diagram of the beam in the direction of z-axis is shown below.
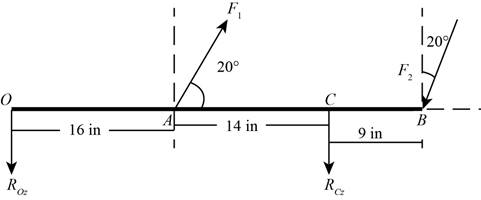
Figure (2)
Write the deflection equation along z-axis for beam 6 and beam 10 using Table A-9.
Here, the force component at point
Write the force component at point
Here, the force component at
Write the force component at point
Here, the force component at
Write the expression for net displacement at point
Here, the net deflection at point
Write the slope equation at along z-axis at point
Here, the slope along z-axis at point is
Write the slope equation at along y-axis at point
Here, the slope along z-axis at point is
Write the expression for the net slope at point
Here, the net slope is
Conclusion:
Substitute
Substitute
Substitute
Substitute
Substitute
Substitute
Substitute
Substitute
Thus, the net displacement of the shaft at point
Substitute
Substitute
Substitute
Thus, the net slope of the shaft at point
Want to see more full solutions like this?
Chapter 4 Solutions
SHIGLEY'S MECH.ENGINEERING DESIGN-EBK>I
- -7 Repeat Problem 2.3-5, but n include the weight of the bar. See Table I-I in Appendix I for the weight density of steel.arrow_forwardA stepped shaft ACE is held against rotation at ends A and B and subjected to a torque T0acting at section C(see figure). The two segments of the shaft (AC and CB) have diameters dAand dg, respectively, and polar moments of inertia IpAand IpBrespectively. The shaft has length L and segment AC has length a. For what ratio a/L will the maximum shear stresses be the same in both segments of the shaft? For what ratio a/L will the internal torques be the same in both segments of the shaft?arrow_forwardCompare the angle of twist 1 for a thin-walled circular tube (see figure) calculated from the approximate theory for thin-walled bars with the angle of twist 2 calculated from the exact theory of torsion for circular bars, Express the ratio 12terms of the non-dimensional ratio ß = r/t. Calculate the ratio of angles of twist for ß = 5, 10, and 20. What conclusion about the accuracy of the approximate theory do you draw from these results?arrow_forward
- Repeat Problem 11.3-9. Use two C 150 × 12.2 steel shapes and assume that E = 205 GPa and L = 6 m.arrow_forwardRepeat Problem 10.4-41 for the loading shown in the figure.arrow_forwardA prismatic bar AB of length L and solid circular cross section (diameter d) is loaded by a distributed torque of constant intensity t per unit distance (sec figure). Determine the maximum shear stress tmaxin the bar. Determine the angle of twist between t the ends of the bar.arrow_forward
- The nonprismalic cantilever circular bar shown has an internal cylindrical hole of diameter dtl From 0 to x so the net area of the cross section n for segment I is A. Load P is applied at x, and load Ptl is applied at x = L. Assume that E is constant. (a) Find reaction force Ry (b) Find internal axial forces Ntin segments I and 2. (c} Find .v required to obtain axial displacement at joint 3 ofarrow_forwardA statically indeterminate stepped shaft ACE is fixed at ends A and B and loaded by a torque TQat point C (see figure). The two segments of the bar are made of the same material, have lengths L4and LB, and have polar moments of inertia IAand Ipb. Determine the angle of rotation 4>of the cross section at Cby using strain energy. Hint: Use Eq, (3-55b) to determine the strain energy Urn terms of the angle d?. Then equate the strain energy to the work done by the torque to. Compare your result with Eq. (3-52) of Example 3-9.arrow_forwardA solid circulai' aluminum bar AB is fixed at both ends and loaded by a uniformly distributed torque 150N·n/m. The bar has diameter d = 30 mm. Calculate the reactive torques at the supports and the angle of twist at midspan. Assume that G = 28 GPa.arrow_forward
- Solve the preceding problem for a steel pipe column (E = 210 GPa) with length L = 1.2 m, inner diameter d2= 36 mm, and outer diameter d2=40 mm.arrow_forwardThe Z-section of Example D-7 is subjected to M = 5 kN · m, as shown. Determine the orientation of the neutral axis and calculate the maximum tensile stress c1and maximum compressive stress ocin the beam. Use the following numerical data: height; = 200 mm, width ft = 90 mm, constant thickness a = 15 mm, and B = 19.2e. Use = 32.6 × 106 mm4 and I2= 2.4 × 10e mm4 from Example D-7arrow_forwardA T-frame structure is torn posed of a prismatic beam ABC and a nonprismatic column DBF. The beam and the column have a pin support at .A and D, respectively. Both members are connected with a pin at B. The lengths and properties of the members are shown in the figure. Find the vertical displacement of the column at points F and B. Plot axial force (AFD) and axial displacement (ADD) diagrams For column DBF.arrow_forward
 Mechanics of Materials (MindTap Course List)Mechanical EngineeringISBN:9781337093347Author:Barry J. Goodno, James M. GerePublisher:Cengage Learning
Mechanics of Materials (MindTap Course List)Mechanical EngineeringISBN:9781337093347Author:Barry J. Goodno, James M. GerePublisher:Cengage Learning
