
Calculus: Early Transcendental Functions
7th Edition
ISBN: 9781337552516
Author: Ron Larson, Bruce H. Edwards
Publisher: Cengage Learning
expand_more
expand_more
format_list_bulleted
Concept explainers
Textbook Question
Chapter 4.7, Problem 37E
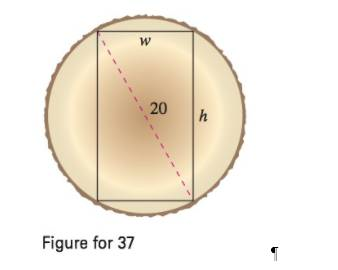
Beam Strength A wooden beam has a rectangular cross section of height h and width w (see figure). The strength. S' of the beam is directly proportional to the width and the square of the height. What are the dimensions of the strongest beam that can be cut from a round log of diameter 20 inches? (Hint:
Expert Solution & Answer
Want to see the full answer?
Check out a sample textbook solution
Chapter 4 Solutions
Calculus: Early Transcendental Functions
Ch. 4.1 - Extreme Value Theorem In your own words, describe...Ch. 4.1 - Maximum What is die difference between a relative...Ch. 4.1 - Critical Numbers Use a graphing utility to graph...Ch. 4.1 - Extrema on a Closed Interval Explain how to find...Ch. 4.1 - The Value of the Derivative at Relative Extrema In...Ch. 4.1 - Prob. 6ECh. 4.1 - The Value of the Derivative at Relative Extrema In...Ch. 4.1 - Prob. 8ECh. 4.1 - The Value of the Derivative at Relative Extrema In...Ch. 4.1 - The Value of the Derivative at Relative Extrema In...
Ch. 4.1 - Approximating Critical Numbers In Exercises 11-14,...Ch. 4.1 - Prob. 12ECh. 4.1 - Approximating Critical Numbers In Exercises 11-14,...Ch. 4.1 - Approximating Critical Numbers In Exercises 11-14,...Ch. 4.1 - Prob. 15ECh. 4.1 - Prob. 16ECh. 4.1 - Finding Critical Numbers In Exercises 15-24, find...Ch. 4.1 - Prob. 18ECh. 4.1 - Finding Critical Numbers In Exercises 15-24, find...Ch. 4.1 - Prob. 20ECh. 4.1 - Prob. 21ECh. 4.1 - Finding Critical Numbers In Exercises 15-24, find...Ch. 4.1 - Prob. 23ECh. 4.1 - Finding Critical Numbers In Exercises 15-24, find...Ch. 4.1 - Finding Extrema on a Closed Interval In Exercises...Ch. 4.1 - Finding Extrema on a Closed Interval In Exercises...Ch. 4.1 - Finding Extrema on a Closed Interval In Exercises...Ch. 4.1 - Prob. 28ECh. 4.1 - Prob. 29ECh. 4.1 - Finding Extrema on a Closed Interval In Exercises...Ch. 4.1 - Finding Extrema on a Closed Interval In Exercises...Ch. 4.1 - Finding Extrema on a Closed Interval In Exercises...Ch. 4.1 - Prob. 33ECh. 4.1 - Finding Extrema on a Closed Interval In Exercises...Ch. 4.1 - Finding Extrema on a Closed Interval In Exercises...Ch. 4.1 - Prob. 36ECh. 4.1 - Prob. 37ECh. 4.1 - Prob. 38ECh. 4.1 - Prob. 39ECh. 4.1 - Finding Extrema on a Closed Interval In Exercises...Ch. 4.1 - Prob. 41ECh. 4.1 - Finding Extrema on a Closed Interval In Exercises...Ch. 4.1 - Prob. 43ECh. 4.1 - Finding Extrema on a Closed Interval In Exercises...Ch. 4.1 - Finding Extrema on a Closed Interval In Exercises...Ch. 4.1 - Prob. 46ECh. 4.1 - Prob. 47ECh. 4.1 - Prob. 48ECh. 4.1 - Finding Extrema on an Interval In Exercises47-50,...Ch. 4.1 - Prob. 50ECh. 4.1 - Prob. 51ECh. 4.1 - Prob. 52ECh. 4.1 - Prob. 53ECh. 4.1 - Prob. 54ECh. 4.1 - Prob. 55ECh. 4.1 - Prob. 56ECh. 4.1 - Finding Extrema Using Technology In Exercises...Ch. 4.1 - Prob. 58ECh. 4.1 - Prob. 59ECh. 4.1 - Prob. 60ECh. 4.1 - Prob. 61ECh. 4.1 - Finding Maximum Values Using Technology In...Ch. 4.1 - Prob. 63ECh. 4.1 - Prob. 64ECh. 4.1 - Think About K Explain why the function f(x)=tanx a...Ch. 4.1 - HOW DO YOU SEE IT? Determine whether each labeled...Ch. 4.1 - Prob. 67ECh. 4.1 - Using Graphs In Exercises 67 and 68, determine...Ch. 4.1 - Prob. 69ECh. 4.1 - Prob. 70ECh. 4.1 - Prob. 71ECh. 4.1 - Lawn Sprinkler A lawn sprinkler is constructed in...Ch. 4.1 - Honeycomb The surface area of a cell in a...Ch. 4.1 - Highway Design la order to build a highway, it is...Ch. 4.1 - Prob. 75ECh. 4.1 - Prob. 76ECh. 4.1 - True or False? In Exercises 75-78, determine...Ch. 4.1 - True or False? In Exercises 75-78, determine...Ch. 4.1 - Functions Let the function f be differentiable on...Ch. 4.1 - Critical Numbers Consider the cubic function...Ch. 4.1 - Determine all real numbers a0 for which there...Ch. 4.2 - Rolle's Theorem In your own words, describe...Ch. 4.2 - Prob. 2ECh. 4.2 - Writing In Exercises 5-6, explain why Rolle's...Ch. 4.2 - Writing In Exercises 5-6, explain why Rolles...Ch. 4.2 - Prob. 5ECh. 4.2 - Writing In Exercises 5-6, explain why Rolle's...Ch. 4.2 - Using Rolle's Theorem In Exercises 7-10, dud the...Ch. 4.2 - Prob. 8ECh. 4.2 - Prob. 9ECh. 4.2 - Prob. 10ECh. 4.2 - Using Rolle's Theorem In Exercises 11-26,...Ch. 4.2 - Using Rolle's Theorem In Exercises 11-26,...Ch. 4.2 - Prob. 13ECh. 4.2 - Prob. 14ECh. 4.2 - Prob. 15ECh. 4.2 - Prob. 16ECh. 4.2 - Prob. 17ECh. 4.2 - Using Rolle's Theorem In Exercises 11-26,...Ch. 4.2 - Using Rolle's Theorem In Exercises 11-26,...Ch. 4.2 - Prob. 20ECh. 4.2 - Prob. 21ECh. 4.2 - Prob. 22ECh. 4.2 - Prob. 23ECh. 4.2 - Prob. 24ECh. 4.2 - Using Rolle's Theorem In Exercises 11-26,...Ch. 4.2 - Prob. 26ECh. 4.2 - Prob. 27ECh. 4.2 - Prob. 28ECh. 4.2 - Prob. 29ECh. 4.2 - Prob. 30ECh. 4.2 - Prob. 31ECh. 4.2 - Using Rolle's Theorem In Exercises 27-32, use a...Ch. 4.2 - Vertical Motion The height of a ball t seconds...Ch. 4.2 - Prob. 34ECh. 4.2 - Prob. 35ECh. 4.2 - Mean Value Theorem In Exercises 35 and36, copy the...Ch. 4.2 - Prob. 37ECh. 4.2 - Writing In Exercises 37-40, explain why the Mean...Ch. 4.2 - Prob. 39ECh. 4.2 - Prob. 40ECh. 4.2 - Prob. 41ECh. 4.2 - Mean Value Theorem Consider the graph of the...Ch. 4.2 - Using the Mean Value Theorem In Exercises 43-56,...Ch. 4.2 - Prob. 44ECh. 4.2 - Prob. 45ECh. 4.2 - Prob. 46ECh. 4.2 - Prob. 47ECh. 4.2 - Using the Mean Value Theorem In Exercises 43-56,...Ch. 4.2 - Prob. 49ECh. 4.2 - Prob. 50ECh. 4.2 - Using the Mean Value Theorem In Exercises 43-56,...Ch. 4.2 - Prob. 52ECh. 4.2 - Prob. 53ECh. 4.2 - Prob. 54ECh. 4.2 - Prob. 55ECh. 4.2 - Prob. 56ECh. 4.2 - Prob. 57ECh. 4.2 - Prob. 58ECh. 4.2 - Prob. 59ECh. 4.2 - Using the Mean Value Theorem In Exercises 57-62,...Ch. 4.2 - Using the Mean Value Theorem In Exercises 57-62,...Ch. 4.2 - Using the Mean Value Theorem In Exercises 57-62,...Ch. 4.2 - Vertical Motion The height of an object r seconds...Ch. 4.2 - Sales A company introduces a new product for which...Ch. 4.2 - Prob. 65ECh. 4.2 - Prob. 66ECh. 4.2 - Prob. 67ECh. 4.2 - Prob. 68ECh. 4.2 - Speed A plane begins its takeoff at 2:00 p.m. on a...Ch. 4.2 - Temperature Wien an object is removed from a...Ch. 4.2 - Prob. 71ECh. 4.2 - Acceleration At 9:13 a.m.. a sports car is...Ch. 4.2 - Think About It Sketch the graph of an arbitrary...Ch. 4.2 - HOW DO YOU SEE IT? The figure shows two pans of...Ch. 4.2 - Prob. 75ECh. 4.2 - Prob. 76ECh. 4.2 - Finding a Solution In Exercises 75-78, use the...Ch. 4.2 - Prob. 78ECh. 4.2 - Prob. 79ECh. 4.2 - Prob. 80ECh. 4.2 - Prob. 81ECh. 4.2 - Prob. 82ECh. 4.2 - Prob. 83ECh. 4.2 - Prob. 84ECh. 4.2 - True or False? In Exercises 83-86, determine...Ch. 4.2 - Prob. 86ECh. 4.2 - Prob. 87ECh. 4.2 - Prob. 88ECh. 4.2 - Prob. 89ECh. 4.2 - Prob. 90ECh. 4.2 - Prob. 91ECh. 4.2 - Prob. 92ECh. 4.2 - Prob. 93ECh. 4.2 - Prob. 94ECh. 4.2 - Prob. 95ECh. 4.3 - CONCEPT CHECK Increasing and Decreasing Functions...Ch. 4.3 - Prob. 2ECh. 4.3 - Using a Graph In Exercises 3 and 4, use the graph...Ch. 4.3 - Prob. 4ECh. 4.3 - Using a Graph In Exercises 5-10, use the graph to...Ch. 4.3 - Using a Graph In Exercises 5-10, use the graph to...Ch. 4.3 - Prob. 7ECh. 4.3 - Using a Graph In Exercises 5-10, use the graph to...Ch. 4.3 - Prob. 9ECh. 4.3 - Prob. 10ECh. 4.3 - Prob. 11ECh. 4.3 - Prob. 12ECh. 4.3 - Intervals on Which a Function Is Increasing or...Ch. 4.3 - Prob. 14ECh. 4.3 - Intervals on Which a Function Is Increasing or...Ch. 4.3 - Intervals on Which a Function Is Increasing or...Ch. 4.3 - Intervals on Which a Function Is Increasing or...Ch. 4.3 - Intervals on Which a Function Is Increasing or...Ch. 4.3 - Prob. 19ECh. 4.3 - Prob. 20ECh. 4.3 - Intervals on Which a Function Is Increasing or...Ch. 4.3 - Prob. 22ECh. 4.3 - Prob. 23ECh. 4.3 - Prob. 24ECh. 4.3 - Prob. 25ECh. 4.3 - Prob. 26ECh. 4.3 - Prob. 27ECh. 4.3 - Prob. 28ECh. 4.3 - Prob. 29ECh. 4.3 - Prob. 30ECh. 4.3 - Prob. 31ECh. 4.3 - Applying the First Derivative Test In Exercises...Ch. 4.3 - Prob. 33ECh. 4.3 - Prob. 34ECh. 4.3 - Prob. 35ECh. 4.3 - Applying the First Derivative Test In Exercises...Ch. 4.3 - Applying the First Derivative Test In Exercises...Ch. 4.3 - Prob. 38ECh. 4.3 - Prob. 39ECh. 4.3 - Prob. 40ECh. 4.3 - Applying the First Derivative Test In Exercises...Ch. 4.3 - Prob. 42ECh. 4.3 - Prob. 43ECh. 4.3 - Prob. 44ECh. 4.3 - Prob. 45ECh. 4.3 - Applying the First Derivative Test In Exercises...Ch. 4.3 - Prob. 47ECh. 4.3 - Applying the First Derivative Test In Exercises...Ch. 4.3 - Prob. 49ECh. 4.3 - Applying the First Derivative Test In Exercises...Ch. 4.3 - Prob. 51ECh. 4.3 - Prob. 52ECh. 4.3 - Prob. 53ECh. 4.3 - Prob. 54ECh. 4.3 - Prob. 55ECh. 4.3 - Prob. 56ECh. 4.3 - Prob. 57ECh. 4.3 - Prob. 58ECh. 4.3 - Prob. 59ECh. 4.3 - Prob. 60ECh. 4.3 - Prob. 61ECh. 4.3 - Prob. 62ECh. 4.3 - Prob. 63ECh. 4.3 - Prob. 64ECh. 4.3 - Prob. 65ECh. 4.3 - Prob. 66ECh. 4.3 - Prob. 67ECh. 4.3 - Prob. 68ECh. 4.3 - Prob. 69ECh. 4.3 - Finding and Analyzing Derivatives Using Technology...Ch. 4.3 - Prob. 71ECh. 4.3 - Prob. 72ECh. 4.3 - Prob. 73ECh. 4.3 - Think About It In Exercises 73-78, the graph of f...Ch. 4.3 - Prob. 75ECh. 4.3 - Think About It In Exercises 73-78, the graph of f...Ch. 4.3 - Prob. 77ECh. 4.3 - Prob. 78ECh. 4.3 - Prob. 79ECh. 4.3 - Prob. 80ECh. 4.3 - Prob. 81ECh. 4.3 - Prob. 82ECh. 4.3 - Prob. 83ECh. 4.3 - Prob. 84ECh. 4.3 - Prob. 85ECh. 4.3 - Prob. 86ECh. 4.3 - Prob. 87ECh. 4.3 - Prob. 88ECh. 4.3 - Prob. 89ECh. 4.3 - Prob. 90ECh. 4.3 - Prob. 91ECh. 4.3 - Prob. 92ECh. 4.3 - Prob. 93ECh. 4.3 - Prob. 94ECh. 4.3 - Prob. 95ECh. 4.3 - Prob. 96ECh. 4.3 - Prob. 97ECh. 4.3 - Prob. 98ECh. 4.3 - Prob. 99ECh. 4.3 - Prob. 100ECh. 4.3 - Prob. 101ECh. 4.3 - Prob. 102ECh. 4.3 - Prob. 103ECh. 4.3 - Creating Polynomial Functions In Exercises...Ch. 4.3 - Prob. 105ECh. 4.3 - Prob. 106ECh. 4.3 - Prob. 107ECh. 4.3 - Prob. 108ECh. 4.3 - Prob. 109ECh. 4.3 - Prob. 110ECh. 4.3 - Prob. 111ECh. 4.3 - Prob. 112ECh. 4.3 - Prob. 113ECh. 4.3 - Prob. 114ECh. 4.3 - Prob. 115ECh. 4.3 - Prob. 116ECh. 4.3 - Prob. 117ECh. 4.3 - Finding Values Consider f(x)=axebx2. Find a and b...Ch. 4.3 - Prob. 119ECh. 4.4 - CONCEPT CHECK Test for Concavity in your own...Ch. 4.4 - Prob. 2ECh. 4.4 - Determining Concavity In Exercises 5-14, determine...Ch. 4.4 - Determining Concavity In Exercises 5-14, determine...Ch. 4.4 - Prob. 5ECh. 4.4 - Prob. 6ECh. 4.4 - Determining Concavity In Exercises 5-14, determine...Ch. 4.4 - Prob. 8ECh. 4.4 - Prob. 9ECh. 4.4 - Determining Concavity In Exercises 5-14, determine...Ch. 4.4 - Prob. 11ECh. 4.4 - Prob. 12ECh. 4.4 - Prob. 13ECh. 4.4 - Prob. 14ECh. 4.4 - Finding Points of Inflection In Exercises 15-36,...Ch. 4.4 - Prob. 16ECh. 4.4 - Finding Points of Inflection In Exercises15-36,...Ch. 4.4 - Prob. 18ECh. 4.4 - Prob. 19ECh. 4.4 - Finding Points of Inflection In Exercises15-36,...Ch. 4.4 - Prob. 21ECh. 4.4 - Prob. 22ECh. 4.4 - Finding Points of Inflection In Exercises15-36,...Ch. 4.4 - Finding Points of Inflection In Exercises15-36,...Ch. 4.4 - Prob. 25ECh. 4.4 - Finding Points of Inflection In Exercises15-36,...Ch. 4.4 - Prob. 27ECh. 4.4 - Prob. 28ECh. 4.4 - Finding Points of Inflection In Exercises15-36,...Ch. 4.4 - Prob. 30ECh. 4.4 - Prob. 31ECh. 4.4 - Prob. 32ECh. 4.4 - Finding Points of Inflection In Exercises15-36,...Ch. 4.4 - Prob. 34ECh. 4.4 - Prob. 35ECh. 4.4 - Finding Points of Inflection In Exercises15-36,...Ch. 4.4 - Prob. 37ECh. 4.4 - Prob. 38ECh. 4.4 - Prob. 39ECh. 4.4 - Prob. 40ECh. 4.4 - Using the Second Derivative Test In Exercises...Ch. 4.4 - Prob. 42ECh. 4.4 - Prob. 43ECh. 4.4 - Prob. 44ECh. 4.4 - Prob. 45ECh. 4.4 - Prob. 46ECh. 4.4 - Prob. 47ECh. 4.4 - Prob. 48ECh. 4.4 - Prob. 49ECh. 4.4 - Prob. 50ECh. 4.4 - Prob. 51ECh. 4.4 - Prob. 52ECh. 4.4 - Prob. 53ECh. 4.4 - Prob. 54ECh. 4.4 - Prob. 55ECh. 4.4 - Prob. 56ECh. 4.4 - Prob. 57ECh. 4.4 - Prob. 58ECh. 4.4 - Prob. 59ECh. 4.4 - Prob. 60ECh. 4.4 - Finding Extrema and Points of Inflection Using...Ch. 4.4 - Prob. 62ECh. 4.4 - Prob. 63ECh. 4.4 - Prob. 64ECh. 4.4 - Sketching Graphs In parts (a) and (b), the graph...Ch. 4.4 - HOW DO YOU SEE IT? Using the graph of f, state the...Ch. 4.4 - Prob. 67ECh. 4.4 - Prob. 68ECh. 4.4 - Prob. 69ECh. 4.4 - Prob. 70ECh. 4.4 - Think About It The figure shows the graph of f....Ch. 4.4 - Think About It Water is running into the vase...Ch. 4.4 - Conjecture Consider the function f(x)=(x2)n. (a)...Ch. 4.4 - Prob. 74ECh. 4.4 - Prob. 75ECh. 4.4 - Prob. 76ECh. 4.4 - Aircraft Glide Path A small aircraft starts its...Ch. 4.4 - Highway Design A section of highway connecting two...Ch. 4.4 - Average Cost A manufacturer has determined that...Ch. 4.4 - Prob. 80ECh. 4.4 - Prob. 81ECh. 4.4 - Modeling Data The average typing speeds S (in...Ch. 4.4 - Prob. 83ECh. 4.4 - Prob. 84ECh. 4.4 - Prob. 85ECh. 4.4 - Prob. 86ECh. 4.4 - Prob. 87ECh. 4.4 - Prob. 88ECh. 4.4 - Prob. 89ECh. 4.4 - Prob. 90ECh. 4.4 - Prob. 91ECh. 4.4 - Prob. 92ECh. 4.4 - Prob. 93ECh. 4.4 - Prob. 94ECh. 4.5 - CONCEPT CHECK Writing Describe in your own words...Ch. 4.5 - Prob. 2ECh. 4.5 - Prob. 3ECh. 4.5 - Prob. 4ECh. 4.5 - Matching In Exercises 5-10, match the function...Ch. 4.5 - Prob. 6ECh. 4.5 - Prob. 7ECh. 4.5 - Matching In Exercises 5-10, match the function...Ch. 4.5 - Prob. 9ECh. 4.5 - Prob. 10ECh. 4.5 - Finding Limits at Infinity In Exercises 11 and 12,...Ch. 4.5 - Finding Limits at Infinity In Exercises 11 and 12,...Ch. 4.5 - Prob. 13ECh. 4.5 - Prob. 14ECh. 4.5 - Finding Limits at Infinity In Exercises 13-16,...Ch. 4.5 - Finding Limits at Infinity In Exercises 13-16,...Ch. 4.5 - Prob. 17ECh. 4.5 - Finding a Limit In Exercises 17-42, find the...Ch. 4.5 - Prob. 19ECh. 4.5 - Finding a Limit In Exercises 17-42, find the...Ch. 4.5 - Prob. 21ECh. 4.5 - Prob. 22ECh. 4.5 - Prob. 23ECh. 4.5 - Finding a Limit In Exercises 17-42, find the...Ch. 4.5 - Prob. 25ECh. 4.5 - Finding a Limit In Exercises 17-42, find the...Ch. 4.5 - Prob. 27ECh. 4.5 - Finding a Limit In Exercises 17-42, find the...Ch. 4.5 - Prob. 29ECh. 4.5 - Finding a Limit In Exercises 17-42, find the...Ch. 4.5 - Finding a Limit In Exercises 17-42, find the...Ch. 4.5 - Prob. 32ECh. 4.5 - Prob. 33ECh. 4.5 - Finding a Limit In Exercises 17-42, find the...Ch. 4.5 - Prob. 35ECh. 4.5 - Finding a Limit In Exercises 17-42, find the...Ch. 4.5 - Prob. 37ECh. 4.5 - Prob. 38ECh. 4.5 - Finding a Limit In Exercises 17-42, find the...Ch. 4.5 - Finding a Limit In Exercises 17-42, find the...Ch. 4.5 - Prob. 41ECh. 4.5 - Prob. 42ECh. 4.5 - Prob. 43ECh. 4.5 - Prob. 44ECh. 4.5 - Prob. 45ECh. 4.5 - Prob. 46ECh. 4.5 - Prob. 47ECh. 4.5 - Prob. 48ECh. 4.5 - Prob. 49ECh. 4.5 - Prob. 50ECh. 4.5 - Prob. 51ECh. 4.5 - Prob. 52ECh. 4.5 - Prob. 53ECh. 4.5 - Prob. 54ECh. 4.5 - Prob. 55ECh. 4.5 - Prob. 56ECh. 4.5 - Engine Efficiency The efficiency (in percent) of...Ch. 4.5 - Physics Newtons First Law of Motion and Einsteins...Ch. 4.5 - Prob. 59ECh. 4.5 - Prob. 60ECh. 4.5 - Prob. 61ECh. 4.5 - HOW DO YOU SEE IT? The graph show the temperature...Ch. 4.5 - Learning Theory In a group project in learning...Ch. 4.5 - Prob. 64ECh. 4.5 - Prob. 65ECh. 4.5 - Using the Definition of Limits at Infinity The...Ch. 4.5 - Using the Definition of Limits at Infinity...Ch. 4.5 - Using the Definition of Limits at Infinity...Ch. 4.5 - Prob. 69ECh. 4.5 - Prob. 70ECh. 4.5 - Prob. 71ECh. 4.5 - Prob. 72ECh. 4.5 - Prob. 73ECh. 4.5 - Distance A line with slope m passes through the...Ch. 4.5 - Prob. 75ECh. 4.5 - Prob. 76ECh. 4.6 - CONCEPT CHECK Analyzing the Graph of a Function...Ch. 4.6 - CONCEPT CHECK Analyzing a Graph Explain how to...Ch. 4.6 - CONCEPT CHECK Slant Asymptote Which type of...Ch. 4.6 - CONCEPT CHECK Polynomial What are the maximum...Ch. 4.6 - Analyzing the Graph of a Function In Exercises...Ch. 4.6 - Analyzing the Graph of a Function In Exercises...Ch. 4.6 - Analyzing the Graph of a Function In Exercises...Ch. 4.6 - Analyzing the Graph of a Function In Exercises...Ch. 4.6 - Analyzing the Graph of a Function In Exercises...Ch. 4.6 - Analyzing the Graph of a Function In Exercises...Ch. 4.6 - Analyzing the Graph of a Function In Exercises...Ch. 4.6 - Analyzing the Graph of a Function In Exercises...Ch. 4.6 - Analyzing the Graph of a Function In Exercises...Ch. 4.6 - Analyzing the Graph of a Function In Exercises...Ch. 4.6 - Analyzing the Graph of a Function In Exercises...Ch. 4.6 - Analyzing the Graph of a Function In Exercises...Ch. 4.6 - Analyzing the Graph of a Function In Exercises...Ch. 4.6 - Analyzing the Graph of a Function In Exercises...Ch. 4.6 - Analyzing the Graph of a Function In Exercises...Ch. 4.6 - Analyzing the Graph of a Function In Exercises...Ch. 4.6 - Analyzing the Graph of a Function In Exercises...Ch. 4.6 - Analyzing the Graph of a Function In Exercises...Ch. 4.6 - Analyzing the Graph of a Function In Exercises...Ch. 4.6 - Analyzing the Graph of a Function In Exercises...Ch. 4.6 - Analyzing the Graph of a Function In Exercises...Ch. 4.6 - Analyzing the Graph of a Function In Exercises...Ch. 4.6 - Analyzing the Graph of a Function In Exercises...Ch. 4.6 - Analyzing the Graph of a Function In Exercises...Ch. 4.6 - Analyzing the Graph of a Function In Exercises...Ch. 4.6 - Analyzing the Graph of a Function In Exercises...Ch. 4.6 - Analyzing the Graph of a Function In Exercises...Ch. 4.6 - Analyzing the Graph of a Function In Exercises...Ch. 4.6 - Analyzing the Graph of a Function In Exercises...Ch. 4.6 - Analyzing the Graph of a Function In Exercises...Ch. 4.6 - Analyzing the Graph of a Trigonometric Function In...Ch. 4.6 - Analyzing the Graph of a Trigonometric Function In...Ch. 4.6 - Analyzing the Graph of a Trigonometric Function In...Ch. 4.6 - Analyzing the Graph of a Trigonometric Function In...Ch. 4.6 - Analyzing the Graph of a Trigonometric Function In...Ch. 4.6 - Analyzing the Graph of a Trigonometric Function In...Ch. 4.6 - Analyzing the Graph of a Trigonometric Function In...Ch. 4.6 - Analyzing the Graph of a Trigonometric Function In...Ch. 4.6 - Analyzing the Graph of a Transcendental Function...Ch. 4.6 - Analyzing the Graph of a Transcendental Function...Ch. 4.6 - Analyzing the Graph of a Transcendental Function...Ch. 4.6 - Analyzing the Graph of a Transcendental Function...Ch. 4.6 - Analyzing the Graph of a Transcendental Function...Ch. 4.6 - Analyzing the Graph of a Transcendental Function...Ch. 4.6 - Analyzing the Graph of a Transcendental Function...Ch. 4.6 - Analyzing the Graph of a Transcendental Function...Ch. 4.6 - Analyzing the Graph of a Transcendental Function...Ch. 4.6 - Analyzing the Graph of a Transcendental Function...Ch. 4.6 - Analyzing the Graph of a Transcendental Function...Ch. 4.6 - Analyzing the Graph of a Transcendental Function...Ch. 4.6 - Analyzing the Graph of a Function Using Technology...Ch. 4.6 - Analyzing the Graph of a Function Using Technology...Ch. 4.6 - Analyzing the Graph of a Function Using Technology...Ch. 4.6 - Prob. 58ECh. 4.6 - Prob. 59ECh. 4.6 - Prob. 60ECh. 4.6 - Prob. 61ECh. 4.6 - Prob. 62ECh. 4.6 - Identifying Graphs In Exercises 63 and 64, the...Ch. 4.6 - Prob. 64ECh. 4.6 - Prob. 65ECh. 4.6 - Graphical Reasoning In Exercises 65-68, use the...Ch. 4.6 - Prob. 67ECh. 4.6 - Prob. 68ECh. 4.6 - Graphical Reasoning Consider the function...Ch. 4.6 - Prob. 70ECh. 4.6 - Prob. 71ECh. 4.6 - Prob. 72ECh. 4.6 - Prob. 73ECh. 4.6 - Prob. 74ECh. 4.6 - EXPLORING CONCEPTS Using a Derivative Let f(t)0...Ch. 4.6 - EXPLORING CONCEPTS Using a Derivative Let f(0)=3...Ch. 4.6 - EXPLORING CONCEPTS A Function and Its Derivative...Ch. 4.6 - HOW DO YOU SEE IT? The graph of f is shown in the...Ch. 4.6 - Prob. 79ECh. 4.6 - Prob. 80ECh. 4.6 - Prob. 81ECh. 4.6 - Prob. 82ECh. 4.6 - Prob. 83ECh. 4.6 - Prob. 84ECh. 4.6 - Prob. 85ECh. 4.6 - Prob. 86ECh. 4.6 - Slant Asymptote In Exercises 85-90, use a graphing...Ch. 4.6 - Prob. 88ECh. 4.6 - Prob. 89ECh. 4.6 - Prob. 90ECh. 4.6 - Investigation Let P(x0,y0) be an arbitrary point...Ch. 4.6 - Graphical Reasoning Identify the real numbers...Ch. 4.6 - Prob. 93ECh. 4.6 - Think About It In Exercises 93-96, create a...Ch. 4.6 - Prob. 95ECh. 4.6 - Prob. 96ECh. 4.6 - Prob. 97ECh. 4.6 - Prob. 98ECh. 4.6 - True or False? In Exercises 97-100, determine...Ch. 4.6 - True or False? In Exercises 97-100, determine...Ch. 4.6 - Graphical Reasoning The graph of the first...Ch. 4.6 - Graphical Reasoning The graph of the first...Ch. 4.6 - Graphical Reasoning Consider the function...Ch. 4.6 - Graphical Reasoning Consider the function...Ch. 4.6 - Prob. 105ECh. 4.6 - Prob. 106ECh. 4.6 - Investigation Consider the function f(x)=2xnx4+1...Ch. 4.6 - PUTNAM EXAM CHALLENGE Let f(x) be defined for axb....Ch. 4.7 - CONCEPT CHECK Writing In your own words, describe...Ch. 4.7 - CONCEPT CHECK Optimization Problems In your own...Ch. 4.7 - Numerical Graphical and Analytic Analysis Find two...Ch. 4.7 - Numerical, Graphical, and Analytic Analysis An...Ch. 4.7 - Finding Numbers In Exercises 5-10, find two...Ch. 4.7 - Prob. 6ECh. 4.7 - Prob. 7ECh. 4.7 - Prob. 8ECh. 4.7 - Prob. 9ECh. 4.7 - Prob. 10ECh. 4.7 - Prob. 11ECh. 4.7 - Maximum Area In Exercises 11 and 12, find the...Ch. 4.7 - Minimum Perimeter In Exercises 13 and 14, find the...Ch. 4.7 - Minimum Perimeter In Exercises 13 and 14, find the...Ch. 4.7 - Minimum Distance In Exercises 15 and 16, find the...Ch. 4.7 - Minimum Distance In Exercises 15 and 16, find the...Ch. 4.7 - Minimum Area A rectangular poster is to contain648...Ch. 4.7 - Minimum Area A rectangular page is to contain36...Ch. 4.7 - Minimum Length A farmer plans to fence a...Ch. 4.7 - Maximum Volume A rectangular solid (with a square...Ch. 4.7 - Maximum Area A Norman window is constructed by...Ch. 4.7 - Maximum Area A rectangle is bounded by the x- and...Ch. 4.7 - Minimum Length and Minimum Area A right triangle...Ch. 4.7 - Maximum Area Find the area of the largest...Ch. 4.7 - Maximum Area A rectangle is bounded by the x-axis...Ch. 4.7 - Prob. 26ECh. 4.7 - Numerical Graphical and Analytic Analysis An...Ch. 4.7 - Numerical, Graphical, and Analytic Analysis A...Ch. 4.7 - Maximum Volume A rectangular package to be sent by...Ch. 4.7 - Maximum Volume Rework Exercise 29 for a...Ch. 4.7 - Prob. 31ECh. 4.7 - EXPLORING CONCEPTS Area and Perimeter The...Ch. 4.7 - Minimum Surface Area A solid is formed by...Ch. 4.7 - Minimum Cost An industrial tank of the shape...Ch. 4.7 - Prob. 35ECh. 4.7 - Maximum Area Twenty feet of wire is to be used to...Ch. 4.7 - Beam Strength A wooden beam has a rectangular...Ch. 4.7 - Minimum Length Two factories are located at the...Ch. 4.7 - Prob. 39ECh. 4.7 - Illumination A light source is located over the...Ch. 4.7 - Minimum Time A man is in a boat 2 miles from the...Ch. 4.7 - Population Growth Fifty elk are introduced into a...Ch. 4.7 - Prob. 43ECh. 4.7 - Minimum Time When light waves traveling in a...Ch. 4.7 - Maximum Volume A sector with central angle is cut...Ch. 4.7 - Area Perform the following steps to find the...Ch. 4.7 - Prob. 47ECh. 4.7 - HOW DO YOU SEE IT? The graph shows the profit P...Ch. 4.7 - Prob. 49ECh. 4.7 - Area Find the area of the largest rectangle that...Ch. 4.7 - Minimum Distance In Exercises 51-53, consider a...Ch. 4.7 - Minimum Distance In Exercises 51-53, consider a...Ch. 4.7 - Minimum Distance In Exercises 51-53, consider a...Ch. 4.7 - Maximum Area Consider a symmetric cross inscribed...Ch. 4.7 - Prob. 55ECh. 4.7 - Prob. 56ECh. 4.7 - Prob. 57ECh. 4.7 - Prob. 58ECh. 4.8 - CONCEPT CHECK Tangent Line Approximations What is...Ch. 4.8 - Prob. 2ECh. 4.8 - Prob. 3ECh. 4.8 - Prob. 4ECh. 4.8 - Prob. 5ECh. 4.8 - Using a Tangent Line Approximation In Exercises...Ch. 4.8 - Prob. 7ECh. 4.8 - Prob. 8ECh. 4.8 - Prob. 9ECh. 4.8 - Using a Tangent Line Approximation In Exercises...Ch. 4.8 - Prob. 11ECh. 4.8 - Using a Tangent Line Approximation In Exercises...Ch. 4.8 - Prob. 13ECh. 4.8 - Prob. 14ECh. 4.8 - Comparing y and dy In Exercises 15-20, use the...Ch. 4.8 - Prob. 16ECh. 4.8 - Prob. 17ECh. 4.8 - Prob. 18ECh. 4.8 - Prob. 19ECh. 4.8 - Prob. 20ECh. 4.8 - Prob. 21ECh. 4.8 - Prob. 22ECh. 4.8 - Prob. 23ECh. 4.8 - Finding a Differential In Exercises 21-32, find...Ch. 4.8 - Prob. 25ECh. 4.8 - Prob. 26ECh. 4.8 - Prob. 27ECh. 4.8 - Prob. 28ECh. 4.8 - Prob. 29ECh. 4.8 - Prob. 30ECh. 4.8 - Prob. 31ECh. 4.8 - Prob. 32ECh. 4.8 - Using Differentials In Exercises 33 and 34, use...Ch. 4.8 - Using Differentials In Exercises 33 and 34, use...Ch. 4.8 - Prob. 35ECh. 4.8 - Prob. 36ECh. 4.8 - Area The measurement of the side of a square floor...Ch. 4.8 - Area The measurements of the base and altitude of...Ch. 4.8 - Prob. 39ECh. 4.8 - Prob. 40ECh. 4.8 - Stopping Distance The total stopping distance T of...Ch. 4.8 - HOW DO YOU SEE IT? The graph shows the profit P...Ch. 4.8 - Pendulum The period of a pendulum is given by...Ch. 4.8 - Prob. 44ECh. 4.8 - Relative Humidity When the dewpoint is 65...Ch. 4.8 - Surveying A surveyor standing 50 feet from the...Ch. 4.8 - Prob. 47ECh. 4.8 - Prob. 48ECh. 4.8 - Prob. 49ECh. 4.8 - Prob. 50ECh. 4.8 - Prob. 51ECh. 4.8 - Prob. 52ECh. 4.8 - Prob. 53ECh. 4.8 - Prob. 54ECh. 4.8 - Prob. 55ECh. 4.8 - Prob. 56ECh. 4.8 - Prob. 57ECh. 4.8 - Prob. 58ECh. 4.8 - True or False? In Exercises 55-59, determine...Ch. 4 - Finding Extrema on a Closed Interval In Exercises...Ch. 4 - Prob. 2RECh. 4 - Prob. 3RECh. 4 - Prob. 4RECh. 4 - Prob. 5RECh. 4 - Prob. 6RECh. 4 - Prob. 7RECh. 4 - Prob. 8RECh. 4 - Prob. 9RECh. 4 - Prob. 10RECh. 4 - Prob. 11RECh. 4 - Prob. 12RECh. 4 - Prob. 13RECh. 4 - Prob. 14RECh. 4 - Prob. 15RECh. 4 - Prob. 16RECh. 4 - Prob. 17RECh. 4 - Prob. 18RECh. 4 - Prob. 19RECh. 4 - Prob. 20RECh. 4 - Intervals on Which a Function Is Increasing or...Ch. 4 - Prob. 22RECh. 4 - Prob. 23RECh. 4 - Prob. 24RECh. 4 - Prob. 25RECh. 4 - Prob. 26RECh. 4 - Prob. 27RECh. 4 - Prob. 28RECh. 4 - Prob. 29RECh. 4 - Prob. 30RECh. 4 - Prob. 31RECh. 4 - Prob. 32RECh. 4 - Prob. 33RECh. 4 - Prob. 34RECh. 4 - Prob. 35RECh. 4 - Prob. 36RECh. 4 - Prob. 37RECh. 4 - Prob. 38RECh. 4 - Prob. 39RECh. 4 - Prob. 40RECh. 4 - Prob. 41RECh. 4 - Prob. 42RECh. 4 - Prob. 43RECh. 4 - Prob. 44RECh. 4 - Prob. 45RECh. 4 - Prob. 46RECh. 4 - Prob. 47RECh. 4 - Prob. 48RECh. 4 - Prob. 49RECh. 4 - Prob. 50RECh. 4 - Prob. 51RECh. 4 - Prob. 52RECh. 4 - Prob. 53RECh. 4 - Prob. 54RECh. 4 - Prob. 55RECh. 4 - Prob. 56RECh. 4 - Prob. 57RECh. 4 - Prob. 58RECh. 4 - Prob. 59RECh. 4 - Prob. 60RECh. 4 - Prob. 61RECh. 4 - Prob. 62RECh. 4 - Prob. 63RECh. 4 - Prob. 64RECh. 4 - Prob. 65RECh. 4 - Prob. 66RECh. 4 - Prob. 67RECh. 4 - Prob. 68RECh. 4 - Prob. 69RECh. 4 - Prob. 70RECh. 4 - Prob. 71RECh. 4 - Prob. 72RECh. 4 - Prob. 73RECh. 4 - Prob. 74RECh. 4 - Prob. 75RECh. 4 - Prob. 76RECh. 4 - Prob. 77RECh. 4 - Prob. 78RECh. 4 - Prob. 79RECh. 4 - Prob. 80RECh. 4 - Prob. 81RECh. 4 - Prob. 82RECh. 4 - Prob. 83RECh. 4 - Prob. 84RECh. 4 - Prob. 85RECh. 4 - Prob. 86RECh. 4 - Prob. 87RECh. 4 - Prob. 88RECh. 4 - Prob. 89RECh. 4 - Prob. 90RECh. 4 - Prob. 91RECh. 4 - Prob. 92RECh. 4 - Finding Numbers Find two positive numbers such...Ch. 4 - Minimum Distance Find the point on the graph of...Ch. 4 - Maximum Area A rancher has 400 feet of fencing...Ch. 4 - Prob. 96RECh. 4 - Minimum Length A right triangle in the first...Ch. 4 - Minimum Length The wall of a building is to be...Ch. 4 - Maximum Length Find the length of the longest pipe...Ch. 4 - Prob. 100RECh. 4 - Maximum Volume Find the volume of the largest...Ch. 4 - Prob. 102RECh. 4 - Prob. 103RECh. 4 - Prob. 104RECh. 4 - Prob. 105RECh. 4 - Prob. 106RECh. 4 - Volume and Surface Area The radius of a sphere is...Ch. 4 - Prob. 108RECh. 4 - Profit The profit P for a company is P=100xex/400...Ch. 4 - Prob. 1PSCh. 4 - Relative Extrema (a) Graph the fourth-degree...Ch. 4 - Relative Minimum Let f(x)=cx+x2. Determine all...Ch. 4 - Prob. 4PSCh. 4 - Prob. 5PSCh. 4 - Illumination The amount of illumination of a...Ch. 4 - Minimum Distance Consider a room in the shape of a...Ch. 4 - Areas of Triangles The line joining P and Q...Ch. 4 - Prob. 9PSCh. 4 - Mean Value Theorem Determine the values a, b, c,...Ch. 4 - Prob. 11PSCh. 4 - Prob. 12PSCh. 4 - Prob. 13PSCh. 4 - Prob. 14PSCh. 4 - Prob. 15PSCh. 4 - Maximum Area The figures show a rectangle, a...Ch. 4 - Prob. 17PSCh. 4 - Prob. 18PSCh. 4 - Prob. 19PS
Knowledge Booster
Learn more about
Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, calculus and related others by exploring similar questions and additional content below.Similar questions
- Hookes Law Hookes Law states that the force needed to keep a spring stretched x units beyond its natural length is directly proportional to x. Here the constant of proportionality is called the spring constant. a Write Hookes Law as an equation. b If a spring has a natural length of 5 cm and a force of 30 N is required to maintain the spring stretched to a length of 9 cm, find the spring constant. c What force is needed to keep the spring stretched to a length of 11 cm?arrow_forwardHubbles Constant Astronomers believe that the universe is expanding and that stellar objects are moving away from us at a radial velocity V proportional to the distance D from Earth to the object. a. Write V as a function of D using H as the constant of proportionality. b. The equation in part a was first discovered by Edwin Hubble in 1929 and is known as Hubbles law. The constant of proportionality H is known as Hubbles constant. The currently accepted value of Hubbles constant is 70 kilometers per second per megaparsec. One megaparsec is about 3.0861019 kilometers. With these units for H, the distance D is measured in megaparsecs, and the velocity V is measured in kilometers per second. The galaxy G2237+305 is about 122.7 megaparsecs from Earth. How fast is G2237+305 receding from Earth? c. One important feature of Hubbles constant is that scientists use it to estimate the age of the universe. The approximate relation is y=1012H Where y is time in years. Hubbles constant is extremely difficult to measure, and Edwin Hubbles best estimate in 1929 was about 530 kilometers per second per megaparsec. What is the approximate age of the universe when this value of H is used? d. The calculation in part c would give scientists some concern, since Earth is thought to be about 4.6 billion years old. What estimate of the age of the universe does the more modern value of 70 kilometers per second per megaparsec give?arrow_forwardKeplers Third Law Keplers Third Law of planetary motion states that the square of the period T of a planet the time it takes for the planet to make a complete revolution about the sun is directly proportional to the cube of its average distance d from the sun. a Express Keplers Third Law as an equation. b Find the constant of proportionality by using the fact that for our planet the period is about 365 days and the average distance is about 93 million miles. c The planet Neptune is about 2.79109 mi from the sun. Find the period of Neptune.arrow_forward
- Kepler’s Third Law Kepler’s Third Law of planetary motion states that the square of the period T of a planet (the time it takes fur the planet to make a complete resolution about the sun) is directly proportional to the cube of its average distance d from the sun. (a) Express Kepler’s Third Law as an equation. (b) Find the constant of proportionality by using the Fact that for our planet the period is about 365 days and the average distance is about 93 million miles (c) The planet Neptune is about 2.79109 mi from the sun. Find the period of Neptune.arrow_forwardFrictional Force The frictional force F between the tires and the road required to keep a car on a curved section of a highway is directly proportional to the square of the speed s of the car. If the speed of the car is doubled, the force will change by what factor?arrow_forward
arrow_back_ios
arrow_forward_ios
Recommended textbooks for you

 Algebra and Trigonometry (MindTap Course List)AlgebraISBN:9781305071742Author:James Stewart, Lothar Redlin, Saleem WatsonPublisher:Cengage Learning
Algebra and Trigonometry (MindTap Course List)AlgebraISBN:9781305071742Author:James Stewart, Lothar Redlin, Saleem WatsonPublisher:Cengage Learning College AlgebraAlgebraISBN:9781305115545Author:James Stewart, Lothar Redlin, Saleem WatsonPublisher:Cengage Learning
College AlgebraAlgebraISBN:9781305115545Author:James Stewart, Lothar Redlin, Saleem WatsonPublisher:Cengage Learning- Algebra & Trigonometry with Analytic GeometryAlgebraISBN:9781133382119Author:SwokowskiPublisher:Cengage
 Functions and Change: A Modeling Approach to Coll...AlgebraISBN:9781337111348Author:Bruce Crauder, Benny Evans, Alan NoellPublisher:Cengage Learning
Functions and Change: A Modeling Approach to Coll...AlgebraISBN:9781337111348Author:Bruce Crauder, Benny Evans, Alan NoellPublisher:Cengage Learning


Algebra and Trigonometry (MindTap Course List)
Algebra
ISBN:9781305071742
Author:James Stewart, Lothar Redlin, Saleem Watson
Publisher:Cengage Learning

College Algebra
Algebra
ISBN:9781305115545
Author:James Stewart, Lothar Redlin, Saleem Watson
Publisher:Cengage Learning

Algebra & Trigonometry with Analytic Geometry
Algebra
ISBN:9781133382119
Author:Swokowski
Publisher:Cengage

Functions and Change: A Modeling Approach to Coll...
Algebra
ISBN:9781337111348
Author:Bruce Crauder, Benny Evans, Alan Noell
Publisher:Cengage Learning
01 - What Is A Differential Equation in Calculus? Learn to Solve Ordinary Differential Equations.; Author: Math and Science;https://www.youtube.com/watch?v=K80YEHQpx9g;License: Standard YouTube License, CC-BY
Higher Order Differential Equation with constant coefficient (GATE) (Part 1) l GATE 2018; Author: GATE Lectures by Dishank;https://www.youtube.com/watch?v=ODxP7BbqAjA;License: Standard YouTube License, CC-BY
Solution of Differential Equations and Initial Value Problems; Author: Jefril Amboy;https://www.youtube.com/watch?v=Q68sk7XS-dc;License: Standard YouTube License, CC-BY