Chapter 6, Problem 4P

(a)

To determine

To show that: The percentage of the volume of the object above the surface of the liquid is $\frac{{\rho }_f-{\rho }_o}{{\rho }_f}\times 100$

Explanation of Solution

Given information:

The buoyant force is $F={\rho }_{f}g{\displaystyle {\int }_{-h}^{0}A\left(y\right)dy}$.

The weight of the object is $W={\rho }_{o}g{\displaystyle {\int }_{-h}^{L-h}A\left(y\right)dy}$.

Calculation:

Consider the volume above the surface as follows:

${\displaystyle {\int }_0^{L-h}A\left(y\right)dy}$ (1)

Modify Equation (1).

${\displaystyle {\int }_0^{L-h}A\left(y\right)dy}={\displaystyle {\int }_{-h}^{L-h}A\left(y\right)dy}-{\displaystyle {\int }_{-h}^{0}A\left(y\right)dy}$

Divide both sides of the Equation by ${\displaystyle {\int }_{-h}^{L-h}A\left(y\right)dy}$ as shown below.

$\frac{{\displaystyle {\int }_0^{L-h}A\left(y\right)dy}}{{\displaystyle {\int }_{-h}^{L-h}A\left(y\right)dy}}=\frac{{\displaystyle {\int }_{-h}^{L-h}A\left(y\right)dy}-{\displaystyle {\int }_{-h}^{0}A\left(y\right)dy}}{{\displaystyle {\int }_{-h}^{L-h}A\left(y\right)dy}}$ (2)

Apply Archimedes Principle as shown below.

$F=W$

Substitute ${\rho }_{f}g{\displaystyle {\int }_{-h}^{0}A\left(y\right)dy}$ for F and ${\rho }_{o}g{\displaystyle {\int }_{-h}^{L-h}A\left(y\right)dy}$ for W in the above Equation.

$\begin{array}{l}{\rho }_{f}g{\displaystyle {\int }_{-h}^{0}A\left(y\right)dy}={\rho }_{o}g{\displaystyle {\int }_{-h}^{L-h}A\left(y\right)dy}\\ {\rho }_f{\displaystyle {\int }_{-h}^{0}A\left(y\right)dy}={\rho }_o{\displaystyle {\int }_{-h}^{L-h}A\left(y\right)dy}\\ {\displaystyle {\int }_{-h}^{0}A\left(y\right)dy}=\frac{{\rho }_o}{{\rho }_f}{\displaystyle {\int }_{-h}^{L-h}A\left(y\right)dy}\end{array}$

Substitute $\frac{{\rho }_o}{{\rho }_f}{\displaystyle {\int }_{-h}^{L-h}A\left(y\right)dy}$ for ${\displaystyle {\int }_{-h}^{0}A\left(y\right)dy}$ in Equation (2).

$\begin{array}{c}\frac{{\displaystyle {\int }_0^{L-h}A\left(y\right)dy}}{{\displaystyle {\int }_{-h}^{L-h}A\left(y\right)dy}}=\frac{{\displaystyle {\int }_{-h}^{L-h}A\left(y\right)dy}-\frac{{\rho }_o}{{\rho }_f}{\displaystyle {\int }_{-h}^{L-h}A\left(y\right)dy}}{{\displaystyle {\int }_{-h}^{L-h}A\left(y\right)dy}}\\ =\frac{{\displaystyle {\int }_{-h}^{L-h}A\left(y\right)dy}\left(1-\frac{{\rho }_o}{{\rho }_f}\right)}{{\displaystyle {\int }_{-h}^{L-h}A\left(y\right)dy}}\\ =1-\frac{{\rho }_o}{{\rho }_f}\\ =\frac{{\rho }_f-{\rho }_o}{{\rho }_f}\end{array}$

Find the percentage of the volume above the surface.

$\text{Percentage}=\frac{{\rho }_f-{\rho }_o}{{\rho }_f}\times 100$

Therefore, the percentage of the volume of the object above the surface of the liquid is $\underset{\_}{\frac{{\rho }_f-{\rho }_o}{{\rho }_f}\times 100}$ is proved.

(b)

To determine

To calculate: The percentage of the volume of an iceberg above the water.

Answer to Problem 4P

The percentage of the volume of an iceberg above the water is $\underset{\_}{11\%}$.

Explanation of Solution

Given information:

The density of ice is $917{\text{kg/m}}^3$.

The density of seawater is $1,030{\text{kg/m}}^3$.

Calculation:

Refer to part (a).

The percentage of the volume of the object above the surface of the liquid is $\text{Percentage}=\frac{{\rho }_f-{\rho }_o}{{\rho }_f}\times 100$.

Substitute $917{\text{kg/m}}^3$ for ${\rho }_o$ and $1030{\text{kg/m}}^3$ for ${\rho }_f$ in the above Equation.

$\begin{array}{c}\text{Percentage}=\frac{1,030-917}{1,030}\times 100\\ =0.1097\times 100\\ =10.97\%\\ =11\%\end{array}$

Therefore, the percentage of the volume of an iceberg above the water is $\underset{\_}{11\%}$.

(c)

To determine

To show: Does the water overflow when the ice melts?

Answer to Problem 4P

The water does not overflow when the ice melts.

Explanation of Solution

Given information:

An ice cube floats in a glass filled to the brim with water.

Calculation:

Let $V_i$ be the volume of the ice and $V_w$ be the volume of the water from melting of ice.

Refer to part (a).

The volume of ice above the surface of the water is $\frac{{\rho }_f-{\rho }_o}{{\rho }_f}{V}_i$.

The volume below the surface of the water is,

$\begin{array}{c}{V}_i-\frac{{\rho }_f-{\rho }_o}{{\rho }_f}{V}_i=\frac{V_i{\rho }_f-V_i{\rho }_f+V_i{\rho }_o}{{\rho }_f}\\ =\frac{{\rho }_o}{{\rho }_f}{V}_i\end{array}$

Suppose the mass of the ice cube is the same as the mass of the water which is formed when the cube melts.

$\begin{array}{l}{\rho }_o{V}_i={\rho }_f{V}_w\\ V_w=\frac{{\rho }_o}{{\rho }_f}{V}_i\end{array}$

So, when the ice cube melts the volume of the resulting water is same as the underwater volume of the ice cube.

Hence, the water does not overflow when the ice melts.

(d)

To determine

To calculate: The work required to completely submerge the sphere.

Answer to Problem 4P

The work required to completely submerge the sphere is $\underset{\_}{1.05\times {10}^3\text{J}}$.

Explanation of Solution

Given information:

A sphere of radius 0.4 m.

Density of the water is $1,000{\text{kg/m}}^3$.

Calculation:

Suppose the height of the exposed part of the ball is y.

Sketch the instant when the height of the exposed part of the ball is y as shown in Figure 1.

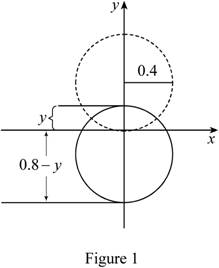
Refer to Figure 1.

$h=0.8-y$

Find the volume of the segment of a sphere as shown below.

$V=\frac{1}{3}\pi h^2\left(3r-h\right)$ (3)

Substitute 0.4 m for r and $\left(0.8-y\right)$ for h in Equation (3).

$\begin{array}{c}V=\frac{1}{3}\pi \times {\left(0.8-y\right)}^2\left(3\times 0.4-\left(0.8-y\right)\right)\\ =\frac{1}{3}\pi \times {\left(0.8-y\right)}^2\left(1.2-\left(0.8-y\right)\right)\end{array}$

Modify the above Equation as shown below.

$\begin{array}{c}V=\frac{1}{3}\pi \times s^2\left(1.2-s\right)\\ =\frac{1}{3}\pi \left(1.2s^2-s^3\right)\end{array}$

Find the work done to submerge the sphere.

$\begin{array}{c}W={\displaystyle {\int }_0^{0.8}1000\times 9.81\times \frac{1}{3}\pi \left(1.2s^2-s^3\right)ds}\\ =10,273\times {\left(1.2\frac{s^3}{3}-\frac{s^4}{4}\right)}_0^{0.8}\\ =10,273\times \left(1.2\times \frac{{0.8}^3}{3}-\frac{{0.8}^4}{4}-0\right)\\ =10,273\times 0.1024\end{array}$

$\begin{array}{c}=1,051.96\text{J}\\ \text{=1}\text{.05}\times {\text{10}}^3\text{J}\end{array}$

Therefore, the work required to completely submerge the sphere is $\underset{\_}{1.05\times {10}^3\text{J}}$.