
In Exercises 13 to 18, find the area of the given
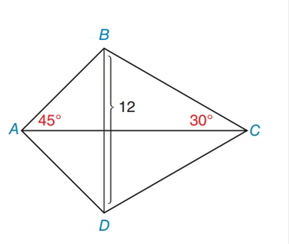
kite
Trending nowThis is a popular solution!

Chapter 8 Solutions
Elementary Geometry for College Students
Additional Math Textbook Solutions
Geometry, Student Edition
McDougal Littell Jurgensen Geometry: Student Edition Geometry
Geometry For Enjoyment And Challenge
EBK STATISTICAL TECHNIQUES IN BUSINESS
Precalculus: Mathematics for Calculus (Standalone Book)
Intermediate Algebra (12th Edition)
- In Exercises 13 to 18, find the area of the given polygon. Kite ABCDarrow_forwardIn Exercises 1 to 8, find the perimeter of each polygon. ABCD with ABBC d1=4md2=10marrow_forwardIn Exercises 47 to 50, use the fact that the area of the polygon is unique. In ABCD,AB=7 and BC=12. The length of altitude AF to side BC is 5. Find the length of altitude AE from A to DC.arrow_forward
- In Exercises 9 to 18, find the areas of the figures shown or described. ABCDarrow_forwardIn Exercises 27 to 30, find the area of the figure shown. Given: In O, OA=5, BC=6, and CD=4 Find: AABCDarrow_forwardIn Exercises 27 to 30, find the area of the figure shown. Given: Hexagon RSTVWX with WV-XT-RS- RS=10 ST=8 TV=5 WV=16 WX-VT- Find: ARSTVWXarrow_forward
- In Exercises 1 to 8, find the perimeter of each polygon.arrow_forwardIn Exercises 9 to 18, find the areas of the figures shown or described. A right triangle has one leg measuring 20 in. and a hypotenuse measuring 29 in.arrow_forwardIn Exercises 27 to 30, find the area of the figure shown. Given: Pentagon RSTVW with mVRS=mVSR=60,RS=82, and RW-WV-VT-TS- Find: ARSTVWarrow_forward
- In Exercises 17 to 30, use the formula A=12aP to find the area of the regular polygon described. Find the area of a regular octagon with an apothem of length a = 9.8 in. and each side of length s = 8.1 in.arrow_forwardIn Review Exercises 15 to 22, state whether the statements are always true A, sometimes true S, or never true N. If a parallelogram is inscribed in a circle, then each of its diagonals must be a diameter.arrow_forwardIn Exercises 32 to 37, write a paragraph proof. Given: RSandTVarediametersofW Prove: RSTVTSarrow_forward
 Elementary Geometry For College Students, 7eGeometryISBN:9781337614085Author:Alexander, Daniel C.; Koeberlein, Geralyn M.Publisher:Cengage,
Elementary Geometry For College Students, 7eGeometryISBN:9781337614085Author:Alexander, Daniel C.; Koeberlein, Geralyn M.Publisher:Cengage, Elementary Geometry for College StudentsGeometryISBN:9781285195698Author:Daniel C. Alexander, Geralyn M. KoeberleinPublisher:Cengage Learning
Elementary Geometry for College StudentsGeometryISBN:9781285195698Author:Daniel C. Alexander, Geralyn M. KoeberleinPublisher:Cengage Learning

