Business
Engineering
Math
Science
Social Science
Elementary Geometry for College St...
Solutions
Elementary Geometry for College St...
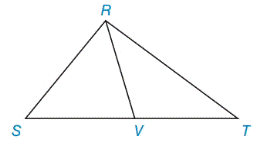
The following problem is based on this theorem: “A median of a triangle separates it into two triangles of equal area.”
In the figure,
a) Explain why
b) If
a)
To explain:
Given,
In figure,
Here,
Since,
Let b be the length of base of
(i.e.)
Then,
(i.e.)
In both triangle of
b)
To find:
Chapter 8 Solutions
Additional Math Solutions
Find more solutions based on key concepts
Show solutions addExpand each expression in Exercises 122. (x+1)(x3)
Applied Calculus
In Exercises 31-34, find an equation of the line that passes through the points. 34. (1, 2) and (3, 4)
Applied Calculus for the Managerial, Life, and Social Sciences: A Brief Approach
Two sociologists administered questionnaires to samples of undergraduates that measured attitudes toward interp...
Essentials Of Statistics
Solving a Linear System Using a Graphing Calculator Solve the system of linear equations by using the r r e f c...
Precalculus: Mathematics for Calculus (Standalone Book)
Starting at a fixed time, each car entering an intersection is observed to see whether it turns left (L), right...
Probability and Statistics for Engineering and the Sciences
In Exercises 2330, factor each expression and simplify as much as possible. (x2+1)(x+1)43(x+1)73
Finite Mathematics
Use Simpsons Rule with n = 10 to approximate the area of the surface obtained by rotating the curve about the x...
Calculus (MindTap Course List)
For the following distribution of quiz scores, how many individuals took the quiz? x f 5 6 4 5 3 5 2 3 1 2 a. 5...
Essentials of Statistics for The Behavioral Sciences (MindTap Course List)
Determining Continuity In Exercises 111122, describe the interval(s) on which the function is continuous. Expla...
Calculus: An Applied Approach (MindTap Course List)
Find an equation for the surface obtained by rotating the curve y=x about the x-axis.
Calculus: Early Transcendentals
If one bushel of corn weighs 56 lb, how many bushels are contained in 14,224 lb or corn?
Elementary Technical Mathematics
BREAK-EVEN POINTS AND MAXIMIZATION 1.The total costs for a company are given by And the total revenues...
Mathematical Applications for the Management, Life, and Social Sciences
Pascals Triangle The triangular pattern in the following figure is known as Pascals triangle. Pascal's triangle...
Mathematical Excursions (MindTap Course List)
Find the most general antiderivative of the function. (Check your answer by differentiation.) f(x)=x23+xx
Single Variable Calculus: Early Transcendentals, Volume I
The distribution of sample means is not always a normal distribution. Under what circumstances is the distribut...
Statistics for The Behavioral Sciences (MindTap Course List)
Finding a Derivative of a Transcendental Function In Exercises 43-60, find the derivative of the transcendental...
Calculus: Early Transcendental Functions
In west Texas, water is extremely important. The following data represent pH levels in groundwater for a random...
Understanding Basic Statistics
Rewrite each expression in Exercises 116 as a single rational expression, simplified as much as possible. 1(x+y...
Finite Mathematics and Applied Calculus (MindTap Course List)
Find the point in which the line with parametric equations x = 2 t, y = 1 + 3t, z = 4t intersects the plane 2x...
Multivariable Calculus
A spherical balloon is being inflated and the radius of the balloon is increasing at a rate of 2 cm/s. (a) Expr...
Single Variable Calculus
For problems 15-26, simplify each numerical expression. Be sure to take advantage of the properties whenever th...
Intermediate Algebra
Finding a Limit In Exercises 41-46, write a simpler function that agrees with the given function at all but one...
Calculus of a Single Variable
For each expression that follows, replace x with 30, y with 45, and z with 60, and then simplify as much as pos...
Trigonometry (MindTap Course List)
What is the maturity value of the following loans? Use to find the maturity values. 5. $15,800 7 4 years _____...
Contemporary Mathematics for Business & Consumers
Determine whether each integral is convergent or divergent. Evaluate those that are convergent. 12. (y33y2)dy
Single Variable Calculus: Early Transcendentals
In Exercises 118, use the techniques presented in this section to find all solutions of the given equation. x31...
Elements Of Modern Algebra
Absolute and Conditional Convergence In your own words, describe the difference between absolute and conditiona...
Calculus: Early Transcendental Functions (MindTap Course List)
The equation of the tangent plane corresponding to (1, 2) to the surface S parameterized by r(u, v) = (u + v)i ...
Study Guide for Stewart's Multivariable Calculus, 8th
Find the periodic payment required to accumulate 50000 over 36 quarters with interest earned at the rate of 378...
Finite Mathematics for the Managerial, Life, and Social Sciences
The solution to xdydx2y=x3 is: a) y=ex3+Cx2 b) y=ex3+x2+C c) y=x3+x2+C d) y=x3+Cx2
Study Guide for Stewart's Single Variable Calculus: Early Transcendentals, 8th
Determine whether each of the following hypotheses is testable and refutable. If not, explain why. a. Young chi...
Research Methods for the Behavioral Sciences (MindTap Course List)
Many families in California are using backyard structures for home offices, art studios, and hobby areas as wel...
STATISTICS F/BUSINESS+ECONOMICS-TEXT
Each of the following common fractions has a denominator that is a power of 10. Write the equivalent decimal fr...
Mathematics For Machine Technology
Write an equation in standard form of each of each ellipse described. Center at (3,4); a=3, b=2;major axis para...
College Algebra (MindTap Course List)
Explain the general advantages and disadvantages of within-subjects designs compared to between-subjects design...
Research Methods for the Behavioral Sciences (MindTap Course List)
Centroid In Exercises 47-52, find the centroid of the solid region hounded by the graphs of the equations or de...
Calculus (MindTap Course List)
True or False? In exercises 67-70, determine whether the statement is true or false. If it is false, explain wh...
Multivariable Calculus
The random variable x is known to be uniformly distributed between 1.0 and 1.5. a. Show the graph of the probab...
Statistics for Business & Economics, Revised (MindTap Course List)
The article Americans are Getting the Wrong Idea on Alcohol and Health (Associated Press, April 19, 2005) repor...
Introduction To Statistics And Data Analysis
