
Interpretation:
To show
To show the Jacobian matrix for the linearization has the form
Here, A and B are
By considering trace and determinant of matrix
To show that depending on the sizes of g and T, the determinant of matrix
By using computer, show that Hopf bifurcation can be supercritical.
Concept Introduction:
To find fixed point of the system, put
Jacobian matrix is used to check the stability of the fixed points, and it is given as:
The system which is settling down to equilibrium by exponentially damping and its decay rate depends on a control parameter
Answer to Problem 17E
Solution:
It is shown that the Jacobian matrix for the linearization has the form
It is shown that all eigenvalues of the matrix
It is shown that values of g and T determine whether the determinant of matrix
It is shown that the system goes through supercritical Hopf bifurcation.
Explanation of Solution
a)
The system equations are:
Assuming that
Here, the condition of
In above equation, L.H.S. and R.H.S. are zero and positive respectively when
Thus, the curves intersect and have unique symmetric solution.
b)
The Jacobian matrix is:
To prove determinant law,
Expanding along last column,
Again expanding along bottom row,
Therefore,
This result is used for calculation of eigenvalues of the
c)
Using determinant is product of the eigenvalues and trace is sum of eigenvalues,
But
Here,
From the above result,
The trace
Thus,
d)
For the matrix
The determinant
And trace
From the above results, the determinant is positive if
Trace can negative or positive depending upon values of b and T.
From the above conclusions of eigenvalues, pitchfork or Hopf bifurcation can occur at the point
By adjusting parameter g, if initially trace is negative, and by varying parameter g, its value is shifting towards positive value, then the pitchfork bifurcation occurs at
By adjusting parameter T, if the determinant is positive, by changing the parameter T, the trace of the matrix changes its sign, then the Hopf bifurcation occurs at a
e)
The plots of
For T being very small, the system is nearly settled down to fixed point

Increasing the value of T, the stable limit cycles just appear.

Further increasing the value of T, the size of the limit cycle increases.
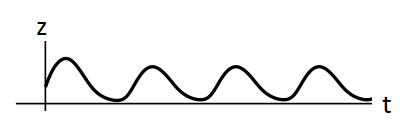
Therefore, the system goes through supercritical Hopf bifurcation.
Want to see more full solutions like this?
Chapter 8 Solutions
Nonlinear Dynamics and Chaos
- For 25 years, Arthur Reynolds and Judy Temple tracked more than 1,400 children who participated in a publicly funded early childhood development program beginning at age 3. They found that children who participated in the program showed higher levels of educational attainment, socioeconomic status, and job skills, as well as lower rates of substance abuse, felony arrest, and incarceration, than those who did not receive school-based early education. One possible theory for the success of this program is that improving school readiness improved the children's success in school. The improved success in school in turn improved their readiness for adulthood, resulting in increased job skills and socioeconomic status as well as lower rates of substance abuse. What is the independent and dependent variable?arrow_forwardExercise 13-4 (LO13-2) The production department of Celltronics International wants to explore the relationship between the number of employees who assemble a subassembly and the number produced. As an experiment, two employees were assigned to assemble the subassemblies. They produced 15 during a one-hour period. Then four employees assembled them. They produced 25 during a one-hour period. The complete set of paired observations follows. Number ofAssemblers One-HourProduction (units) 2 15 4 25 1 10 5 40 3 30 The dependent variable is production; that is, it is assumed that different levels of production result from a different number of employees. Draw a scatter diagram. Please state exact coordinates Based on the scatter diagram, does there appear to be any relationship between the number of assemblers and production? Compute the coefficient correlation. (Negative values should be…arrow_forward1.11 Buteyko method, scope of inference: Exercise 1.4 introduces a study on using the Buteyko shallow breathing technique to reduce asthma symptoms and improve quality of life. As part of this study 600 asthma patients aged 18-69 who relied on medication for asthma treatment were recruited and randomly assigned to two groups: one practiced the Buteyko method and the other did not. Those in the Buteyko group experienced, on average, a significant reduction in asthma symptoms and an improvement in quality of life. a) Identify the population of interest and the sample in the study. b) Comment on whether or not the results of the study can be generalized to the population, and if the findings of the study can be used to establish causal relationships.arrow_forward
- In a study with a non-directional hypothesis… A) There are two rejection regions that have the same area that adds up to the alpha level. B) There is a single rejection region with an area that corresponds to the alpha level. C) There are two rejection regions that have the same area that adds up to the p-value. D) There is a single rejection region with an area that corresponds to the p-value.arrow_forward27. An article in Radio Engineering and Electronic Physics (1980, Vol. 25, pp. 74-79) investigated the behavior of a stochastic generator in the presence of external noise. The number of periods was measured in a sample of 100 trains for each of two different levels of noise voltage, 100 and 150 mV. For 100 mV, the mean number of periods in a train was 7.9 with s1 = 2.6. For 150 mV, the mean was 6.9 with s2 = 2.4. Use α = 0.01 and assume that each population is normally distributed and the two population variances are equal. (a) It was originally suspected that raising noise voltage would reduce mean number of periods. Do the data support this claim? (b) Calculate a confidence interval to answer the question in part (a).arrow_forwardA test of body reaction to the Malaysian citizens who have taken their vaccine was conducted. Selected citizens who got side effect are categorised according to their blood type and the type of vaccine received. From a sample of 250 citizens, 150 of them were administered with Sinovac while the rest received AstraZeneca. Table 4 shows the number of citizens who had side effect after being vaccinated. Type of vaccine Blood type A B AB O Sinovac 50 M 50 20 AstraZeneca 30 20 20 N Does different blood type among people who had side effect relate to the type of vaccinereceived at A=0.025?arrow_forward
- Show what correction (using the generalized least squares method) we should use if the form of heteroskedasticity was the following, show mathematically For both a) and b)arrow_forwardA developmental psychologist experiment to determine if exposure to an enriched environment shortly after birth will cause increased brain development. Twenty, two-month-old rats are randomly selected from a pool of one thousand two-month-old rat pups. Ten of the twenty pups are exposed to an enriched environment for three weeks and the other ten to the usual environment for the same period of time. At a suitable time after the exposure, the psychologist measures the number of neurons per cm3 in each rat's brain. A comparison is then made of the mean number of neurons per cm3 for each group.a. What is the population?b. What is the independent variable?c. What is the sample?d. What is the statistics?e. What is the dependent variable?arrow_forwardAn article in Biotechnology Progress [“Optimization of Conditions for Bacteriocin Extraction in PEG/Salt Aqueous Two-Phase Systems Using Statistical Experimental Designs” (2001, Vol. 17, pp. 366–368)] reported an experiment to investigate and optimize the extraction of nisin in aqueous two-phase systems (ATPS). Nisin recovery was the dependent variable (y). The two regressor variables were the concentration (%) of PEG 4000 (indicated as x1) and the concentration (%) of Na2SO4 (indicated as x2). The data is shown below. a) Find the fit parameters of the proposed model. b) Establish, by means of a hypothesis test, if the regression is significant. c) State, if the regression coefficients are significant. d) Evaluate R2 as well as R_adjusted^2. e) Construct and analyze the residual plot.arrow_forward
- A local church is interested in determining how length of residence in the present community relates to church attendance. Using a random sample of 15 individuals, they gathered data on how many times in the previous 5 weeks each individual attended church services. The data are provided below. Length of residence in the community Less than 2 years 2-5 years More than 5 years 0 0 1 1 2 3 3 3 3 4 4 4 4 5 4 Using the 5-step model, determine whether and how church attendance is related to length of residence in the community. Use 5% and 1% levels of statistical significance. What are the assumptions for this problem?arrow_forwardIn the simple linear regression model , the Gauss Markov ( classical ) assumptions guarantee that the OLS estimator of the unknown parameters is BLUE. Among those assumptions , in order to have consistency of the OLS estimator we need ( this is a question on the necessary condition ): Question 4Select one: a. we need that the errors are not correlated with each others and that they have zero mean b. we need that the errors are homoscedastic ( all have the same variance) c. we need that the residuals are not correlated with the explanatory variables and that the residuals have zero mean d. we need that the errors have zero mean and that they are not correlated with the regressors ( no endogeneity) e. we need that the errors are homoscedastic ( all have the same variance) and not correlated with each others ( no serial correlation)arrow_forwardData have been collected on the weekly sales of Zippy Chippy, a silicon valley firm, and on whether the U.S economy was rising to a cycle peak, at a cycle peak ,falling to a cycle trough, or at a cycle trough. The results are: Weekly chip sales High Medium Low Total 20 7 3 30 40 30 20 8 2 30 5 5 Economy at peak 30 at trough 100 at rising 30 at falling 40 Total 100 60 40 200 for exercise above:…arrow_forward
 Advanced Engineering MathematicsAdvanced MathISBN:9780470458365Author:Erwin KreyszigPublisher:Wiley, John & Sons, Incorporated
Advanced Engineering MathematicsAdvanced MathISBN:9780470458365Author:Erwin KreyszigPublisher:Wiley, John & Sons, Incorporated Numerical Methods for EngineersAdvanced MathISBN:9780073397924Author:Steven C. Chapra Dr., Raymond P. CanalePublisher:McGraw-Hill Education
Numerical Methods for EngineersAdvanced MathISBN:9780073397924Author:Steven C. Chapra Dr., Raymond P. CanalePublisher:McGraw-Hill Education Introductory Mathematics for Engineering Applicat...Advanced MathISBN:9781118141809Author:Nathan KlingbeilPublisher:WILEY
Introductory Mathematics for Engineering Applicat...Advanced MathISBN:9781118141809Author:Nathan KlingbeilPublisher:WILEY Mathematics For Machine TechnologyAdvanced MathISBN:9781337798310Author:Peterson, John.Publisher:Cengage Learning,
Mathematics For Machine TechnologyAdvanced MathISBN:9781337798310Author:Peterson, John.Publisher:Cengage Learning,






