Algebra and Trigonometry (MindTap Course List)
Algebra and Trigonometry (MindTap Course List)
4th Edition
ISBN: 9781305071742
Author: James Stewart, Lothar Redlin, Saleem Watson
Publisher: Cengage Learning
bartleby

Concept explainers

Vertices Of An Ellipse
In the study of the conic section of the geometry, An ellipse is a plane curve surrounding two focal points, or foci where the set of all locus of points in the plane has their sum of the distances to the two foci is constant. On the ellipse curve, it is…
bartleby

Videos

Textbook Question
Book Icon
Chapter 12.2, Problem 64E

How Wide Is an Ellipse at a Focus? A latus rectum for an ellipse is a line segment perpendicular to the major axis at a focus, with endpoints on the ellipse, as shown in the figure. Show that the length of a latus rectum is 2 b 2 / a for the ellipse

x 2 a 2 + y 2 b 2 = 1 a > b

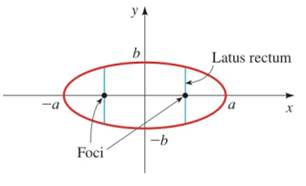
Chapter 12.2, Problem 64E, How Wide Is an Ellipse at a Focus? A latus rectum for an ellipse is a line segment perpendicular to

Expert Solution & Answer
Check Mark

Want to see the full answer?

Check out a sample textbook solution
Blurred answer
Previous
Chapter 12.2, Problem 63E
Next
Chapter 12.2, Problem 65E

Chapter 12 Solutions

Algebra and Trigonometry (MindTap Course List)

Ch. 12.1 - A parabola is the set of all points in the plane...Ch. 12.1 - Prob. 2ECh. 12.1 - Prob. 3ECh. 12.1 - Prob. 4ECh. 12.1 - Prob. 5ECh. 12.1 - Prob. 6ECh. 12.1 - 5-10 Graphs of Parabolas Match the equation with...Ch. 12.1 - Prob. 8ECh. 12.1 - 5-10 Graphs of Parabolas Match the equation with...Ch. 12.1 - Prob. 10E
Ch. 12.1 - Prob. 11ECh. 12.1 - Prob. 12ECh. 12.1 - 11-24 Graphing Parabolas An equation of a parabola...Ch. 12.1 - 11-24 Graphing Parabolas An equation of a parabola...Ch. 12.1 - Prob. 15ECh. 12.1 - 11-24 Graphing Parabolas An equation of a parabola...Ch. 12.1 - Prob. 17ECh. 12.1 - Prob. 18ECh. 12.1 - 11-24 Graphing Parabolas An equation of a parabola...Ch. 12.1 - 11-24 Graphing Parabolas An equation of a parabola...Ch. 12.1 - Prob. 21ECh. 12.1 - Prob. 22ECh. 12.1 - Prob. 23ECh. 12.1 - 11-24 Graphing Parabolas An equation of a parabola...Ch. 12.1 - 25-30 Graphing Parabolas Use a graphing device to...Ch. 12.1 - Prob. 26ECh. 12.1 - Prob. 27ECh. 12.1 - Prob. 28ECh. 12.1 - Prob. 29ECh. 12.1 - Prob. 30ECh. 12.1 - 31-48 Finding the Equation of a Parabola Find an...Ch. 12.1 - Prob. 32ECh. 12.1 - Prob. 33ECh. 12.1 - 31-48 Finding the Equation of a Parabola Find an...Ch. 12.1 - Prob. 35ECh. 12.1 - 31-48 Finding the Equation of a Parabola Find an...Ch. 12.1 - 31-48 Finding the Equation of a Parabola Find an...Ch. 12.1 - Prob. 38ECh. 12.1 - Prob. 39ECh. 12.1 - Prob. 40ECh. 12.1 - Prob. 41ECh. 12.1 - Prob. 42ECh. 12.1 - 31-48 Finding the Equation of a Parabola Find an...Ch. 12.1 - 31-48 Finding the Equation of a Parabola Find an...Ch. 12.1 - Prob. 45ECh. 12.1 - 31-48 Finding the Equation of a Parabola Find an...Ch. 12.1 - Prob. 47ECh. 12.1 - Prob. 48ECh. 12.1 - 49-58 Finding the Equation of a Parabola Find an...Ch. 12.1 - 49-58 Finding the Equation of a Parabola Find an...Ch. 12.1 - Prob. 51ECh. 12.1 - Prob. 52ECh. 12.1 - 49-58 Finding the Equation of a Parabola Find an...Ch. 12.1 - Prob. 54ECh. 12.1 - 49-58 Finding the Equation of a Parabola Find an...Ch. 12.1 - 49-58 Finding the Equation of a Parabola Find an...Ch. 12.1 - 49-58 Finding the Equation of a Parabola Find an...Ch. 12.1 - 49-58 Finding the Equation of a Parabola Find an...Ch. 12.1 - SKILLS 59-60 Families of Parabolasa Find equations...Ch. 12.1 - SKILLS 59-60 Families of Parabolas a Find...Ch. 12.1 - APPLICATIONS Parabolic Reflector A lamp with a...Ch. 12.1 - APPLICATIONS Satellite Dish A reflector for a...Ch. 12.1 - APPLICATIONS Suspension Bridge In a suspension...Ch. 12.1 - Prob. 64ECh. 12.1 - DISCUSS WRITE: Parabolas in the Real World Several...Ch. 12.1 - Prob. 66ECh. 12.2 - CONCEPTS An ellipse is the set of all points in...Ch. 12.2 - Prob. 2ECh. 12.2 - Prob. 3ECh. 12.2 - Prob. 4ECh. 12.2 - Prob. 5ECh. 12.2 - Prob. 6ECh. 12.2 - SKILLS 5-8Graphs of Ellipses Match the equation...Ch. 12.2 - Prob. 8ECh. 12.2 - Prob. 9ECh. 12.2 - Prob. 10ECh. 12.2 - Prob. 11ECh. 12.2 - Prob. 12ECh. 12.2 - SKILLS 9-28 Graphing Ellipse An equation of an...Ch. 12.2 - SKILLS 9-28 Graphing Ellipse An equation of an...Ch. 12.2 - Prob. 15ECh. 12.2 - SKILLS Graphing Ellipse An equation of an ellipse...Ch. 12.2 - Prob. 17ECh. 12.2 - Prob. 18ECh. 12.2 - SKILLS 9-28 Graphing Ellipses An equation of an...Ch. 12.2 - SKILLS 9-28 Graphing Ellipses An equation of an...Ch. 12.2 - Prob. 21ECh. 12.2 - Prob. 22ECh. 12.2 - Prob. 23ECh. 12.2 - Prob. 24ECh. 12.2 - 9-28. Graphing Ellipses An equation of ellipse is...Ch. 12.2 - 9-28. Graphing Ellipses An equation of ellipse is...Ch. 12.2 - Prob. 27ECh. 12.2 - Prob. 28ECh. 12.2 - Prob. 29ECh. 12.2 - Prob. 30ECh. 12.2 - 29-34 Finding the Equation of an Ellipse Find an...Ch. 12.2 - 29-34 Finding the Equation of an Ellipse Find an...Ch. 12.2 - Prob. 33ECh. 12.2 - Prob. 34ECh. 12.2 - Prob. 35ECh. 12.2 - Prob. 36ECh. 12.2 - 35-38 Graphing Ellipses Use a graphing device to...Ch. 12.2 - Prob. 38ECh. 12.2 - Prob. 39ECh. 12.2 - 39-56 Finding the Equation of an Ellipse Find an...Ch. 12.2 - Prob. 41ECh. 12.2 - Prob. 42ECh. 12.2 - 39-56 Finding the Equation of an Ellipse Find an...Ch. 12.2 - 39-56 Finding the Equation of an Ellipse Find an...Ch. 12.2 - Prob. 45ECh. 12.2 - Prob. 46ECh. 12.2 - Prob. 47ECh. 12.2 - 39-56 Finding the Equation of an Ellipse Find an...Ch. 12.2 - 39-56 Finding the Equation of an Ellipse Find an...Ch. 12.2 - Prob. 50ECh. 12.2 - Prob. 51ECh. 12.2 - Prob. 52ECh. 12.2 - Prob. 53ECh. 12.2 - SKILLS 39-56 Finding the Equation of an Ellipse...Ch. 12.2 - SKILLS 39-56 Finding the Equation of an Ellipse...Ch. 12.2 - Prob. 56ECh. 12.2 - Prob. 57ECh. 12.2 - Prob. 58ECh. 12.2 - Prob. 59ECh. 12.2 - Prob. 60ECh. 12.2 - SKILLS Plus Ancillary Circle The ancillary circle...Ch. 12.2 - Prob. 62ECh. 12.2 - Prob. 63ECh. 12.2 - How Wide Is an Ellipse at a Focus? A latus rectum...Ch. 12.2 - APPLICATIONS Perihelion and Aphelion The planets...Ch. 12.2 - Prob. 66ECh. 12.2 - APPLICATIONS Lunar Orbit For an object in an...Ch. 12.2 - Plywood Ellipse A carpenter wishes to construct an...Ch. 12.2 - Prob. 69ECh. 12.2 - Prob. 70ECh. 12.2 - Prob. 71ECh. 12.2 - DISCUSS Is It an Ellipse? A piece of paper is...Ch. 12.3 - CONCEPTS A Hyperbola is the set of all points in...Ch. 12.3 - Prob. 2ECh. 12.3 - Prob. 3ECh. 12.3 - Prob. 4ECh. 12.3 - Prob. 5ECh. 12.3 - Prob. 6ECh. 12.3 - SKILLS Graphs of Hyperbolas Match the equation...Ch. 12.3 - Prob. 8ECh. 12.3 - Prob. 9ECh. 12.3 - Prob. 10ECh. 12.3 - Prob. 11ECh. 12.3 - Graphing Hyperbolas An equation of a hyperbola is...Ch. 12.3 - Graphing Hyperbolas An equation of a hyperbola is...Ch. 12.3 - Prob. 14ECh. 12.3 - Prob. 15ECh. 12.3 - SKILLS 926Graphing HyperbolasAn equation of a...Ch. 12.3 - Prob. 17ECh. 12.3 - SKILLS 926Graphing Hyperbolas An equation of a...Ch. 12.3 - SKILLS 926Graphing Hyperbolas An equation of a...Ch. 12.3 - Prob. 20ECh. 12.3 - Prob. 21ECh. 12.3 - SKILLS 926Graphing Hyperbolas An equation of a...Ch. 12.3 - Prob. 23ECh. 12.3 - SKILLS 926Graphing Hyperbolas An equation of a...Ch. 12.3 - SKILLS 926Graphing Hyperbolas An equation of a...Ch. 12.3 - Prob. 26ECh. 12.3 - Prob. 27ECh. 12.3 - Prob. 28ECh. 12.3 - Prob. 29ECh. 12.3 - Prob. 30ECh. 12.3 - Prob. 31ECh. 12.3 - 27-32. Finding the equation of a Hyperbola Find...Ch. 12.3 - Prob. 33ECh. 12.3 - Prob. 34ECh. 12.3 - Prob. 35ECh. 12.3 - Prob. 36ECh. 12.3 - 37-50. Finding the Equation of a Hyperbola Find an...Ch. 12.3 - Prob. 38ECh. 12.3 - Prob. 39ECh. 12.3 - 37-50 Finding the equation of a HyperbolaFind the...Ch. 12.3 - Prob. 41ECh. 12.3 - Prob. 42ECh. 12.3 - 37-50 Finding the equation of a Hyperbola Find an...Ch. 12.3 - 37-50 Finding the equation of a Hyperbola Find an...Ch. 12.3 - Prob. 45ECh. 12.3 - Prob. 46ECh. 12.3 - Prob. 47ECh. 12.3 - Prob. 48ECh. 12.3 - 37-50 Finding the equation of a Hyperbola Find an...Ch. 12.3 - Prob. 50ECh. 12.3 - Prob. 51ECh. 12.3 - Prob. 52ECh. 12.3 - Prob. 53ECh. 12.3 - Prob. 54ECh. 12.3 - Prob. 55ECh. 12.3 - Prob. 56ECh. 12.3 - Comet Trajectories Some comets, such as Halleys...Ch. 12.3 - Prob. 58ECh. 12.3 - Prob. 59ECh. 12.3 - Prob. 60ECh. 12.4 - Suppose we want to graph an equation in x and y. a...Ch. 12.4 - Prob. 2ECh. 12.4 - Prob. 3ECh. 12.4 - Prob. 4ECh. 12.4 - Prob. 5ECh. 12.4 - Prob. 6ECh. 12.4 - SKILLS 5-12 Graphing Shifted Ellipses An equation...Ch. 12.4 - Prob. 8ECh. 12.4 - Prob. 9ECh. 12.4 - Prob. 10ECh. 12.4 - Prob. 11ECh. 12.4 - Prob. 12ECh. 12.4 - SKILLS 13-20 Graphing Shifted Parabolas An...Ch. 12.4 - Prob. 14ECh. 12.4 - Prob. 15ECh. 12.4 - Prob. 16ECh. 12.4 - Prob. 17ECh. 12.4 - Prob. 18ECh. 12.4 - SKILLS 13-20 Graphing Shifted Parabolas An...Ch. 12.4 - SKILLS 13-20 Graphing Shifted Parabolas An...Ch. 12.4 - Prob. 21ECh. 12.4 - Prob. 22ECh. 12.4 - Prob. 23ECh. 12.4 - Prob. 24ECh. 12.4 - 21-28 Graphing Shifted HyperbolasAn equation of...Ch. 12.4 - Prob. 26ECh. 12.4 - Prob. 27ECh. 12.4 - Prob. 28ECh. 12.4 - Prob. 29ECh. 12.4 - Prob. 30ECh. 12.4 - Prob. 31ECh. 12.4 - Prob. 32ECh. 12.4 - Prob. 33ECh. 12.4 - Prob. 34ECh. 12.4 - Prob. 35ECh. 12.4 - Prob. 36ECh. 12.4 - 35-46Finding the Equation of a Shifted Conic Find...Ch. 12.4 - Prob. 38ECh. 12.4 - 35-46Finding the Equation of a Shifted Conic Find...Ch. 12.4 - Prob. 40ECh. 12.4 - Prob. 41ECh. 12.4 - Prob. 42ECh. 12.4 - Prob. 43ECh. 12.4 - Prob. 44ECh. 12.4 - Prob. 45ECh. 12.4 - Prob. 46ECh. 12.4 - Prob. 47ECh. 12.4 - Prob. 48ECh. 12.4 - SKILLS 47-58 Graphing Shifted Conics Complete the...Ch. 12.4 - Prob. 50ECh. 12.4 - Prob. 51ECh. 12.4 - Prob. 52ECh. 12.4 - Prob. 53ECh. 12.4 - Prob. 54ECh. 12.4 - 47-58 Graphing Shifted Conics Complete the square...Ch. 12.4 - SKILLS 47-58 Graphing Shifted Conics Complete the...Ch. 12.4 - Prob. 57ECh. 12.4 - Prob. 58ECh. 12.4 - Prob. 59ECh. 12.4 - Prob. 60ECh. 12.4 - 59-62. Graphing Shifting Conics Use a graphing...Ch. 12.4 - Prob. 62ECh. 12.4 - Prob. 63ECh. 12.4 - Prob. 64ECh. 12.4 - Prob. 65ECh. 12.4 - Prob. 66ECh. 12.4 - Orbit of a satellite A satellite is in an...Ch. 12.4 - DISCUSS: A Family of Confocal Conics Conics that...Ch. 12.5 - Suppose the x- and y-axes are routed through an...Ch. 12.5 - Prob. 2ECh. 12.5 - Prob. 3ECh. 12.5 - Prob. 4ECh. 12.5 - Prob. 5ECh. 12.5 - Prob. 6ECh. 12.5 - Prob. 7ECh. 12.5 - 3-8 Rotation of Axes Determine the XY-coordinates...Ch. 12.5 - Prob. 9ECh. 12.5 - Prob. 10ECh. 12.5 - Prob. 11ECh. 12.5 - Prob. 12ECh. 12.5 - Prob. 13ECh. 12.5 - Prob. 14ECh. 12.5 - Prob. 15ECh. 12.5 - Prob. 16ECh. 12.5 - Prob. 17ECh. 12.5 - Prob. 18ECh. 12.5 - Prob. 19ECh. 12.5 - Prob. 20ECh. 12.5 - Prob. 21ECh. 12.5 - 15-28 Graphing a Rotated Conic a Use the...Ch. 12.5 - Prob. 23ECh. 12.5 - Prob. 24ECh. 12.5 - Prob. 25ECh. 12.5 - Prob. 26ECh. 12.5 - Prob. 27ECh. 12.5 - Prob. 28ECh. 12.5 - Prob. 29ECh. 12.5 - Prob. 30ECh. 12.5 - Prob. 31ECh. 12.5 - Prob. 32ECh. 12.5 - Prob. 33ECh. 12.5 - Prob. 34ECh. 12.5 - Prob. 35ECh. 12.5 - Prob. 36ECh. 12.5 - Prob. 37ECh. 12.5 - Prob. 38ECh. 12.5 - Prob. 39ECh. 12.6 - CONCEPTS All conics can be described geometrically...Ch. 12.6 - Prob. 2ECh. 12.6 - Prob. 3ECh. 12.6 - Prob. 4ECh. 12.6 - Prob. 5ECh. 12.6 - Prob. 6ECh. 12.6 - Prob. 7ECh. 12.6 - Prob. 8ECh. 12.6 - Prob. 9ECh. 12.6 - Prob. 10ECh. 12.6 - Prob. 11ECh. 12.6 - Prob. 12ECh. 12.6 - Prob. 13ECh. 12.6 - Prob. 14ECh. 12.6 - Prob. 15ECh. 12.6 - Prob. 16ECh. 12.6 - Prob. 17ECh. 12.6 - Prob. 18ECh. 12.6 - Prob. 19ECh. 12.6 - Prob. 20ECh. 12.6 - Prob. 21ECh. 12.6 - Prob. 22ECh. 12.6 - Prob. 23ECh. 12.6 - Prob. 24ECh. 12.6 - Prob. 25ECh. 12.6 - Prob. 26ECh. 12.6 - Prob. 27ECh. 12.6 - Prob. 28ECh. 12.6 - Prob. 29ECh. 12.6 - Prob. 30ECh. 12.6 - Prob. 31ECh. 12.6 - Prob. 32ECh. 12.6 - Prob. 33ECh. 12.6 - Prob. 34ECh. 12.6 - Prob. 35ECh. 12.6 - Prob. 36ECh. 12.6 - Prob. 37ECh. 12.6 - Prob. 38ECh. 12.6 - Prob. 39ECh. 12.6 - Prob. 40ECh. 12.6 - Prob. 41ECh. 12.6 - Prob. 42ECh. 12.6 - Prob. 43ECh. 12.6 - Prob. 44ECh. 12.6 - Prob. 45ECh. 12.6 - Prob. 46ECh. 12.6 - Prob. 47ECh. 12.CR - Prob. 1CCCh. 12.CR - Prob. 2CCCh. 12.CR - a Give the geometric definition of a hyperbola. b...Ch. 12.CR - Prob. 4CCCh. 12.CR - Prob. 5CCCh. 12.CR - Prob. 6CCCh. 12.CR - Prob. 7CCCh. 12.CR - Prob. 8CCCh. 12.CR - Prob. 1ECh. 12.CR - Prob. 2ECh. 12.CR - Prob. 3ECh. 12.CR - Prob. 4ECh. 12.CR - Prob. 5ECh. 12.CR - Prob. 6ECh. 12.CR - Prob. 7ECh. 12.CR - Prob. 8ECh. 12.CR - Prob. 9ECh. 12.CR - Prob. 10ECh. 12.CR - Prob. 11ECh. 12.CR - Prob. 12ECh. 12.CR - Prob. 13ECh. 12.CR - Prob. 14ECh. 12.CR - Prob. 15ECh. 12.CR - Prob. 16ECh. 12.CR - Prob. 17ECh. 12.CR - Prob. 18ECh. 12.CR - Prob. 19ECh. 12.CR - Prob. 20ECh. 12.CR - Prob. 21ECh. 12.CR - Prob. 22ECh. 12.CR - Prob. 23ECh. 12.CR - Prob. 24ECh. 12.CR - Prob. 25ECh. 12.CR - Prob. 26ECh. 12.CR - Prob. 27ECh. 12.CR - Prob. 28ECh. 12.CR - Prob. 29ECh. 12.CR - Prob. 30ECh. 12.CR - Prob. 31ECh. 12.CR - Prob. 32ECh. 12.CR - Prob. 33ECh. 12.CR - Prob. 34ECh. 12.CR - Prob. 35ECh. 12.CR - Prob. 36ECh. 12.CR - Prob. 37ECh. 12.CR - Prob. 38ECh. 12.CR - Prob. 39ECh. 12.CR - Prob. 40ECh. 12.CR - Prob. 41ECh. 12.CR - Prob. 42ECh. 12.CR - Prob. 43ECh. 12.CR - Prob. 44ECh. 12.CR - Prob. 45ECh. 12.CR - Prob. 46ECh. 12.CR - Prob. 47ECh. 12.CR - Prob. 48ECh. 12.CR - Prob. 49ECh. 12.CR - Prob. 50ECh. 12.CR - 43-54 Indentifying and Graphic a conicDetermine...Ch. 12.CR - Prob. 52ECh. 12.CR - Prob. 53ECh. 12.CR - Prob. 54ECh. 12.CR - Prob. 55ECh. 12.CR - Prob. 56ECh. 12.CR - Prob. 57ECh. 12.CR - Prob. 58ECh. 12.CR - Prob. 59ECh. 12.CR - Prob. 60ECh. 12.CR - Prob. 61ECh. 12.CR - Prob. 62ECh. 12.CR - Prob. 63ECh. 12.CR - Prob. 64ECh. 12.CR - Prob. 65ECh. 12.CR - Prob. 66ECh. 12.CR - Prob. 67ECh. 12.CR - Prob. 68ECh. 12.CR - Prob. 69ECh. 12.CR - Prob. 70ECh. 12.CR - Prob. 71ECh. 12.CR - Prob. 72ECh. 12.CR - Prob. 73ECh. 12.CR - Prob. 74ECh. 12.CR - Prob. 75ECh. 12.CR - Prob. 76ECh. 12.CR - Prob. 77ECh. 12.CR - Prob. 78ECh. 12.CR - Prob. 79ECh. 12.CR - Prob. 80ECh. 12.CT - Prob. 1CTCh. 12.CT - Prob. 2CTCh. 12.CT - Prob. 3CTCh. 12.CT - Prob. 4CTCh. 12.CT - Prob. 5CTCh. 12.CT - Find an equation for the hyperbola with foci (0,5)...Ch. 12.CT - 7-9 Find an equation for the conic whose graph is...Ch. 12.CT - Prob. 8CTCh. 12.CT - Prob. 9CTCh. 12.CT - Prob. 10CTCh. 12.CT - 10-12 Determine whether the equation represents...Ch. 12.CT - Prob. 12CTCh. 12.CT - Prob. 13CTCh. 12.CT - Find an equation for the parabola with focus (2,4)...Ch. 12.CT - A parabolic reflector for a car headlight forms a...Ch. 12.CT - aUse the discriminant to determine whether the...Ch. 12.CT - Prob. 17CTCh. 12.FOM - Prob. 1PCh. 12.FOM - Prob. 2PCh. 12.FOM - Prob. 3PCh. 12.FOM - Prob. 4PCh. 12.FOM - Prob. 5PCh. 12.FOM - Prob. 6P

Additional Math Textbook Solutions

Find more solutions based on key concepts
For each of the following linear operators L on 2 , determine the matrix A representing L with respect to e1,e2...

Linear Algebra with Applications (9th Edition) (Featured Titles for Linear Algebra (Introductory))

Consider the subspaceim(A) of 2 , where A=[2436] . Find a basis of ker(AT) , and draw a sketch illustratingthe ...

Linear Algebra with Applications (2-Download)

The largest polynomial that divides evenly into a list of polynomials is called the _______.

Elementary & Intermediate Algebra

In Exercises 17—82, add or subtract as indicated. Simplify the result, if possible. 56. yy2+5y+6+4y2y6

Introductory Algebra for College Students (7th Edition)

NOTE: Write your answers using interval notation when appropriate. CHECKING ANALYTIC SKILLS Fill in each blank ...

Graphical Approach To College Algebra

Subtract. Check each answer by adding. a. 12-9 b. 22-7 c. 35-35 d. 70-0

Prealgebra (7th Edition)

Knowledge Booster
Background pattern image
Algebra
Learn more about
Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, algebra and related others by exploring similar questions and additional content below.
Similar questions
Recommended textbooks for you
Text book image
College Algebra
Algebra
ISBN:9781305115545
Author:James Stewart, Lothar Redlin, Saleem Watson
Publisher:Cengage Learning
Text book image
Algebra and Trigonometry (MindTap Course List)
Algebra
ISBN:9781305071742
Author:James Stewart, Lothar Redlin, Saleem Watson
Publisher:Cengage Learning
Text book image
College Algebra (MindTap Course List)
Algebra
ISBN:9781305652231
Author:R. David Gustafson, Jeff Hughes
Publisher:Cengage Learning
Text book image
College Algebra
Algebra
ISBN:9781337282291
Author:Ron Larson
Publisher:Cengage Learning
Text book image
College Algebra
Algebra
ISBN:9781938168383
Author:Jay Abramson
Publisher:OpenStax
Text book image
Intermediate Algebra
Algebra
ISBN:9780998625720
Author:Lynn Marecek
Publisher:OpenStax College
SEE MORE TEXTBOOKS
What is Ellipse?; Author: Don't Memorise;https://www.youtube.com/watch?v=nzwCInIMlU4;License: Standard YouTube License, CC-BY