EBK NUMERICAL METHODS FOR ENGINEERS
7th Edition
ISBN: 9780100254145
Author: Chapra
Publisher: YUZU
expand_more
expand_more
format_list_bulleted
Videos
Textbook Question
Chapter 16, Problem 32P
In a similar fashion to the case study described in Sec. 16.4, develop the potential energy function for the system depictedin Fig.P16.32. Develop cont our and surface plotsin MATLAB. Minimize the potential energy function in order to determine the equilibrium displacements
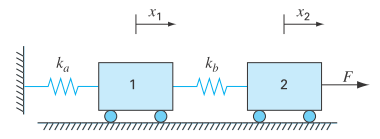
FIGURE P16.32
Two frictionless masses connected to a wall by a pair of linear elastic springs.
Expert Solution & Answer
Want to see the full answer?
Check out a sample textbook solution
Students have asked these similar questions
A schematic diagram of the knee joint is shown in Fig, where Cdenotes the effective center of rotation of the knee and P is the point of insertion of the quadriceps tendon to the patella. The distance from C to P is 10 cm. The quadriceps, responsible for extension of the knee, are known to produce maximum isometric tetanic tension at an effective optimal length of 30 cm. This occurs when the knee flexion angle, θ, is 45◦. Obtaining muscle performance data from the appropriate figure in this chapter, determine the range of knee flexion angles for which the quadriceps produce an isometric tetanic tension at least 80% of maximal. Hint: be careful to use radians (rather than degrees) in this question when appropriate.
An object of mass m and homogeneous structure given below is in equilibrium between two springs and a
damper in the vertical direction. Under the influence of the disrupting force F(t), the system is set in motion.
Here, the mass of the system will be taken as m=4 (kg), k1-95800 N/m and k2= 1706 (N/m), c=704
(Ns/m).
a) For the case where the input of the request is F(t) and the output is y1, find the
transfer function Y1(s)/ F(s).
b) Calculate the zeros and poles of the system using the transfer function you
found..
m
K₂
F(t)
K₁
A
B
Y₂
A wind turbine testing laboratory provided the following results results: • Speed in the feed section = VA • Speed in the discharge section = VD • Feed (cross-section) area = A • Static pressure in the supply section = PA • Temperature in the feed section = T • Static pressure in the discharge section = Patm Estimate the reaction (strength) that the wind turbine will exert on the support with the information you collected in the tests. Take on that the air behaves like a perfect gas.
Chapter 16 Solutions
EBK NUMERICAL METHODS FOR ENGINEERS
Ch. 16 - 16.1 Design the optimal cylindrical container...Ch. 16 - 16.2 (a) Design the optimal conical container...Ch. 16 - Design the optimal cylindrical tank with...Ch. 16 - The specific growth rate of a yeast that produces...Ch. 16 - A chemical plant makes three major products on a...Ch. 16 - 16.6 Recently chemical engineers have become...Ch. 16 - 16.7 A mixture of benzene and toluene are to be...Ch. 16 - 16.8 A compound A will be converted into B in a...Ch. 16 - In problem 16.8, only one reactor is used. If two...Ch. 16 - 16.10 For the reaction:
equilibrium can be...
Ch. 16 - A chemical plant requires 106L/day of a solution....Ch. 16 - You must design a triangular open channel to carry...Ch. 16 - 16.13 As an agricultural engineer, you must design...Ch. 16 - 16.14 Find the optimal dimensions for a heated...Ch. 16 - A finite-element model of a cantilever beam...Ch. 16 - 16.16 Suppose that you are asked to design a...Ch. 16 - TheStreeter-Phelps model can be used to compute...Ch. 16 - Prob. 18PCh. 16 - 16.19 The flow in an open channel can be predicted...Ch. 16 - A cylindrical beam carries a compression load...Ch. 16 - The Splash River has a flow rate of 2106m3/d, of...Ch. 16 - 16.22 Determine the beam cross-sectional areas...Ch. 16 - AtotalchargeQ is uniformly distributed around a...Ch. 16 - A system consist softwopower plants that must...Ch. 16 - 16.25 The torque transmitted to an induction motor...Ch. 16 - (a) A computer equipment manufacture rproduces...Ch. 16 - A manufacturer provides specialized microchips....Ch. 16 - 16.28 The total drag on an airfoil can be...Ch. 16 - Mechanical/Aerospace Engineering
16.29 Roller...Ch. 16 - 16.30 An aerospace company is developing a new...Ch. 16 - 16.31 A manufacturing firm produces four types of...Ch. 16 - In a similar fashion to the case study described...Ch. 16 - 16.33 Recent interest in competitive and...
Knowledge Booster
Learn more about
Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, mechanical-engineering and related others by exploring similar questions and additional content below.Similar questions
- The mass of Block(A) in Fig. below is( 6 kg ).The coefficient of friction between the block and the surface on which it rests is (0.25) .The weight (w) is (12N) and the system is in Equilibrium.(a)Find the friction force exerted on Block( A).//(b) Find the maximum weight of (W) for which the system will remain in Equilibriumarrow_forward68% @ uw 10:12 * Asiacell 1ı, docs.google.com 2. If a wooden block of weight W = 9.7 N placed on a smooth surface inclined at an angle 35 and is at rest, then the reaction (F) offered by the surface is * F 35° - 5.6 N ON 9.8 N 7.9 N 13. Find the angle between the horizontal and vertical forces acting in the given figure consisting of a beam with various sections.arrow_forward4. The specific weight of water in the ocean may be calculated from the empirical relation: y = y + Kh/2 (in which h is the depth below the ocean surface, and K is an empirical constant for seawater). Drive an expression for the pressure, P, at any depth h. Find the specific weight and pressure at a depth of 2.0 miles, assuming yo-64 lb/ft³, h in feet, and K = 0.025 lb/ft³.arrow_forward
- A fender is mounted on a automobile though dampers (to absorb collision energy) and springs (so that the fender can recover after low-speed collisions). During a crash-test, the automobile is moving at 2 m/s when its fender strikes a concrete barrier. The vehicle mass, m, is 1,000 kg. (In comparison, the fender itself is essentially massless.) The springs that mount the fender have a stiffness, k, of 1,000,000 N/m. y m barrier 1) Write a differential equation for the deflection of the springs when the fender is in contact with the barrier. 2) If the damping coefficient, c, is 30,000 N-s/m, what is the damping ratio of the mass-spring-damper system when the fender is in contact with the barrier? 3) For that damping coefficient, make a reasonably accurate sketch (with properly labeled axes) of the time-course of the force exerted on the barrier, starting from the moment of first contact. 4) Is there any value of the damping coefficient, c, that would yield no rebound of the vehicle from…arrow_forwardA three wheeled OTV has been designed such that the forces from the wheels and motors are uniform, hence the reaction forces at the point of contact with the upper surface can be modeled as a single vertical reaction support. The platform is a square with side length 200mm and has a thickness of 20mm. Plywood has a density of 0.37 g/cm^3. For the purposes of finding the platform weight, W, ignore any holes in the plywood for motor mounts. Due to a misscommunication in the team, the motor mounts M1, M2, and M3 were not attached symmetrically! The potential consequences of this are a difference in reaction forces at the platform to keep it balanced. This difference in reaction forces will result a different normal force at each wheel, and hence the potential for different traction forces, leading to an inability to drive the OTV straight. • F₁: (-75,-75) F₂: (85,-75) F: (15,85) P WEDNE 0 Bottom view 0 M2 A coordinate system has been defined, such that middle of the board is 0,0. In this…arrow_forwardA three wheeled OTV has been designed such that the forces from the wheels and motors are uniform, hence the reaction forces at the point of contact with the upper surface can be modeled as a single vertical reaction support. The platform is a square with side length 200mm and has a thickness of 20mm. Plywood has a density of 0.3 g/cm^3. For the purposes of finding the platform weight, W, ignore any holes in the plywood for motor mounts. Due to a misscommunication in the team, the motor mounts M1, M2, and M3 were not attached symmetrically! The potential consequences of this are a difference in reaction forces at the platform to keep it balanced. This difference in reaction forces will result a different normal force at each wheel, and hence the potential for different traction forces, leading to an inability to drive the OTV straight. Co • F: (-75,-75) F₂: (85, -75) • F3: (15,85) -17.4319 MAT 1.338758 3.18886 7 Top View A coordinate system has been defined, such that middle of the…arrow_forward
- (b) Figure Q.3(b) shows a 510 kg balloon with buoyancy force of F = 6 kN, and the air resistance is Fb = 100y N, where v is veloceity in m/s. (1) Draw a free body diagram and the kinetic diagram of the balloon. (ii) Express the acceleration of the balloon in term of v. (ii) If the balloon starts from rest, find the velocity of the balloon. UNIVERSITIT (iv) Using the expression of velocity obtained in (iii, determine the maximum velocity of the balloon. Fp = (100v)N F 6 kN Figure Q.3(b) ALAYSIA KERANA TUHarrow_forwardExample 1: Four masses m1, m2, m3, m4 are 200 kg. 300 kg. 240 kg and 260 kg, respectively. The corresponding radii of rotation are 0.2, 0.15, 0.25 and 0.3 meters, respectively, and the angles between successive masses are 45°, 75° and 135°. Find the position and magnitude of the balance mass required, if its radius of rotation is set to 0.2 m.arrow_forwardFind the equation of pressure, P exerted by a fluid as a function of density, r, gravity, g and height of the fluid, h.arrow_forward
- X₁ Find expression for X2 K₁ K₂ K3 00000 m, 00000 m₂ 00000 In the figure above, mass m1 = m2 and the spring constants k1=k3. When mass m1 is displaced slightly by a distance. x1, from equillibrium as shown, m2 also displaces by x2. a) the potential energy of the system, U(x1,x2)arrow_forwardE3. Suppose a mass-spring system is described by the ODE u"+9u = 0 with initial conditions u(0) = -1, and u' (0)I= 0. %3D a) How high up and how far down does the mass go? b) What is the velocity of the mass when it passes through equilibrium? c) Will the mass move slower as it passes through equilibrium the 5th time it passes through compared to the 1st time? d) Show that the time between a high point and the subsequent low point is 1/2 the period. e) Show that the time between a high point and the subsequent passage through equilibrium is 1/4 the period. (You might need the identity: arctan(2) + arctan(1/z) = /2.)arrow_forwardA mass of 300g hangs in a spring with a spring stiffness of 40 N/m (same situation as in Exercise 4.6). The mass is connected to the spring with a weightless cord, the rigidity of the cord can be considered infinite, ie it is so large that it does not affect the rigidity of the system. We start with a situation where the spring is not loaded and the weight is placed at the end of the spring. So the weight is ground free so that it falls from a height equal to the length of the string before it starts to act on the spring. 0 cm, 6.0 cm, 12 cm, 24 cm. That is, for situations when the length of the cord is 0 cm, 6.0 cm, 12 cm and 24 cm.arrow_forward
arrow_back_ios
SEE MORE QUESTIONS
arrow_forward_ios
Recommended textbooks for you
Elements Of ElectromagneticsMechanical EngineeringISBN:9780190698614Author:Sadiku, Matthew N. O.Publisher:Oxford University Press
Mechanics of Materials (10th Edition)Mechanical EngineeringISBN:9780134319650Author:Russell C. HibbelerPublisher:PEARSON
Thermodynamics: An Engineering ApproachMechanical EngineeringISBN:9781259822674Author:Yunus A. Cengel Dr., Michael A. BolesPublisher:McGraw-Hill Education
Control Systems EngineeringMechanical EngineeringISBN:9781118170519Author:Norman S. NisePublisher:WILEY
Mechanics of Materials (MindTap Course List)Mechanical EngineeringISBN:9781337093347Author:Barry J. Goodno, James M. GerePublisher:Cengage Learning
Engineering Mechanics: StaticsMechanical EngineeringISBN:9781118807330Author:James L. Meriam, L. G. Kraige, J. N. BoltonPublisher:WILEY
Elements Of Electromagnetics
Mechanical Engineering
ISBN:9780190698614
Author:Sadiku, Matthew N. O.
Publisher:Oxford University Press
Mechanics of Materials (10th Edition)
Mechanical Engineering
ISBN:9780134319650
Author:Russell C. Hibbeler
Publisher:PEARSON
Thermodynamics: An Engineering Approach
Mechanical Engineering
ISBN:9781259822674
Author:Yunus A. Cengel Dr., Michael A. Boles
Publisher:McGraw-Hill Education
Control Systems Engineering
Mechanical Engineering
ISBN:9781118170519
Author:Norman S. Nise
Publisher:WILEY
Mechanics of Materials (MindTap Course List)
Mechanical Engineering
ISBN:9781337093347
Author:Barry J. Goodno, James M. Gere
Publisher:Cengage Learning
Engineering Mechanics: Statics
Mechanical Engineering
ISBN:9781118807330
Author:James L. Meriam, L. G. Kraige, J. N. Bolton
Publisher:WILEY
Trigonometry - Harmonic Motion - Equation Setup; Author: David Hays;https://www.youtube.com/watch?v=BPrZnn3DJ6Q;License: Standard YouTube License, CC-BY
Simple Harmonic Motion - An introduction : ExamSolutions Maths Revision; Author: ExamSolutions;https://www.youtube.com/watch?v=tH2vldyP5OE;License: Standard YouTube License, CC-BY