
Single Variable Calculus: Early Transcendentals, Volume I
8th Edition
ISBN: 9781305270343
Author: James Stewart
Publisher: Cengage Learning
expand_more
expand_more
format_list_bulleted
Concept explainers
Textbook Question
Chapter 4.4, Problem 6E
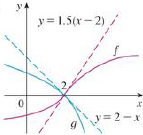
Use the graphs of f and g and their tangent lines at (2, 0) to find
Expert Solution & Answer
Want to see the full answer?
Check out a sample textbook solution
Students have asked these similar questions
Find the slope of the tangent line to the parabola y=4x-x^2 at the point (1,3)
1) using the definition: m=lim->a f(x)-f(a)/x-a
2)using the equation: m=lim->0 f(a+h)-f(a)/h
Use the definition of the derivative to evaluate
lim In(2+h) - In(2)/h
h approaches 0
Use the limit definition to find the slope of the tangent line to the graph of f at the given point.
f(x) = 17 − x2, (4, 1)
Chapter 4 Solutions
Single Variable Calculus: Early Transcendentals, Volume I
Ch. 4.1 - Explain the difference between an absolute minimum...Ch. 4.1 - Prob. 2ECh. 4.1 - Prob. 3ECh. 4.1 - Prob. 4ECh. 4.1 - Use the graph to state the absolute and local...Ch. 4.1 - Use the graph to state the absolute and local...Ch. 4.1 - Sketch the graph of a function f that is...Ch. 4.1 - Sketch the graph of a function f that is...Ch. 4.1 - Prob. 9ECh. 4.1 - Prob. 10E
Ch. 4.1 - (a) Sketch the graph of a function that has a...Ch. 4.1 - (a) Sketch the graph of a function on [1, 2] that...Ch. 4.1 - (a) Sketch the graph of a function on [1, 2] that...Ch. 4.1 - (a) Sketch the graph of a function that has two...Ch. 4.1 - Sketch the graph of f by hand and use your sketch...Ch. 4.1 - Prob. 16ECh. 4.1 - Prob. 17ECh. 4.1 - Prob. 18ECh. 4.1 - Prob. 19ECh. 4.1 - Prob. 20ECh. 4.1 - Prob. 21ECh. 4.1 - Prob. 22ECh. 4.1 - Prob. 23ECh. 4.1 - Prob. 24ECh. 4.1 - Prob. 25ECh. 4.1 - Prob. 26ECh. 4.1 - Prob. 27ECh. 4.1 - Prob. 28ECh. 4.1 - Prob. 29ECh. 4.1 - Prob. 30ECh. 4.1 - Prob. 31ECh. 4.1 - Prob. 32ECh. 4.1 - Prob. 33ECh. 4.1 - Prob. 34ECh. 4.1 - Prob. 35ECh. 4.1 - Prob. 36ECh. 4.1 - Prob. 37ECh. 4.1 - Prob. 38ECh. 4.1 - Prob. 39ECh. 4.1 - Prob. 40ECh. 4.1 - Prob. 41ECh. 4.1 - Prob. 42ECh. 4.1 - Prob. 43ECh. 4.1 - Prob. 44ECh. 4.1 - A formula for the derivative of a function f is...Ch. 4.1 - A formula for the derivative of a function f is...Ch. 4.1 - Find the absolute maximum and absolute minimum...Ch. 4.1 - Find the absolute maximum and absolute minimum...Ch. 4.1 - Find the absolute maximum and absolute minimum...Ch. 4.1 - Find the absolute maximum and absolute minimum...Ch. 4.1 - Find the absolute maximum and absolute minimum...Ch. 4.1 - Find the absolute maximum and absolute minimum...Ch. 4.1 - Find the absolute maximum and absolute minimum...Ch. 4.1 - Find the absolute maximum and absolute minimum...Ch. 4.1 - Find the absolute maximum and absolute minimum...Ch. 4.1 - Find the absolute maximum and absolute minimum...Ch. 4.1 - Find the absolute maximum and absolute minimum...Ch. 4.1 - Find the absolute maximum and absolute minimum...Ch. 4.1 - Find the absolute maximum and absolute minimum...Ch. 4.1 - Find the absolute maximum and absolute minimum...Ch. 4.1 - Find the absolute maximum and absolute minimum...Ch. 4.1 - Find the absolute maximum and absolute minimum...Ch. 4.1 - If a and b are positive numbers, find the maximum...Ch. 4.1 - Use a graph to estimate the critical numbers of...Ch. 4.1 - Prob. 65ECh. 4.1 - (a) Use a graph to estimate the absolute maximum...Ch. 4.1 - (a) Use a graph to estimate the absolute maximum...Ch. 4.1 - (a) Use a graph to estimate the absolute maximum...Ch. 4.1 - After the consumption of an alcoholic beverage,...Ch. 4.1 - After an antibiotic tablet is taken, the...Ch. 4.1 - Between 0C and 30C, the volume V (in cubic...Ch. 4.1 - An object with weight W is dragged along a...Ch. 4.1 - The water level, measured in feet above mean sea...Ch. 4.1 - On May 7, 1992, the space shuttle Endeavour was...Ch. 4.1 - Prob. 75ECh. 4.1 - Prob. 76ECh. 4.1 - Prob. 77ECh. 4.1 - Prob. 78ECh. 4.1 - Prob. 79ECh. 4.1 - A cubic function is a polynomial of degree 3; that...Ch. 4.2 - The graph of a function f is shown. Verify that f...Ch. 4.2 - Draw the graph of a function defined on [0, 8]...Ch. 4.2 - The graph of a function g is shown. (a) Verify...Ch. 4.2 - Draw the graph of a function that is continuous on...Ch. 4.2 - Verify that the function satisfies the three...Ch. 4.2 - Verify that the function satisfies the three...Ch. 4.2 - Verify that the function satisfies the three...Ch. 4.2 - Verify that the function satisfies the three...Ch. 4.2 - Let f(x) = 1 x2/3. Show that f(l) = f(1) but...Ch. 4.2 - Let f(x) = tan x. Show that f(0) = f() but there...Ch. 4.2 - Verify that the function satisfies the hypotheses...Ch. 4.2 - Verify that the function satisfies the hypotheses...Ch. 4.2 - Verify that the function satisfies the hypotheses...Ch. 4.2 - Verify that the function satisfies the hypotheses...Ch. 4.2 - Find the number c that satisfies the conclusion of...Ch. 4.2 - Find the number c that satisfies the conclusion of...Ch. 4.2 - Let f(x) = (x 3)2. Show that there is no value of...Ch. 4.2 - Let f(x) = 2 |2x 1|. Show that there is no value...Ch. 4.2 - Show that the equation has exactly one real root....Ch. 4.2 - Show that the equation has exactly one real root....Ch. 4.2 - Show that the equation x3 15x + c = 0 has at most...Ch. 4.2 - Show that the equation x4 + 4x + c = 0 has at most...Ch. 4.2 - (a) Show that a polynomial of degree 3 has at most...Ch. 4.2 - Prob. 24ECh. 4.2 - Prob. 25ECh. 4.2 - Prob. 26ECh. 4.2 - Does there exist a function f such that f(0) = 1,...Ch. 4.2 - Prob. 28ECh. 4.2 - Show that sin x x if 0 x 2.Ch. 4.2 - Prob. 30ECh. 4.2 - Prob. 31ECh. 4.2 - If f(x) = c (c a constant) for all x, use...Ch. 4.2 - Prob. 33ECh. 4.2 - Use the method of Example 6 to prove the identity...Ch. 4.2 - Prob. 36ECh. 4.2 - Prob. 37ECh. 4.2 - A number a is called a fixed point of a function f...Ch. 4.3 - Use the given graph of f to find the following....Ch. 4.3 - Prob. 2ECh. 4.3 - Prob. 3ECh. 4.3 - Prob. 4ECh. 4.3 - The graph of the derivative f of a function f is...Ch. 4.3 - The graph of the derivative f of a function f is...Ch. 4.3 - In each part state the x-coordinates of the...Ch. 4.3 - The graph of the first derivative f of a function...Ch. 4.3 - (a) Find the intervals on which f is increasing or...Ch. 4.3 - Prob. 10ECh. 4.3 - Prob. 11ECh. 4.3 - (a) Find the intervals on which f is increasing or...Ch. 4.3 - Prob. 13ECh. 4.3 - Prob. 14ECh. 4.3 - Prob. 15ECh. 4.3 - Prob. 16ECh. 4.3 - Prob. 17ECh. 4.3 - Prob. 18ECh. 4.3 - Prob. 19ECh. 4.3 - Prob. 20ECh. 4.3 - Prob. 21ECh. 4.3 - Prob. 22ECh. 4.3 - Prob. 23ECh. 4.3 - Prob. 24ECh. 4.3 - Prob. 25ECh. 4.3 - Prob. 26ECh. 4.3 - Prob. 27ECh. 4.3 - Prob. 28ECh. 4.3 - Prob. 29ECh. 4.3 - Prob. 30ECh. 4.3 - Sketch the graph of a function that satisfies all...Ch. 4.3 - Prob. 32ECh. 4.3 - Suppose f is a continuous function where f(x) 0...Ch. 4.3 - The graph of a function y = f(x) is shown. At...Ch. 4.3 - The graph of the derivative f of a continuous...Ch. 4.3 - The graph of the derivative f of a continuous...Ch. 4.3 - (a) Find the intervals of increase or decrease....Ch. 4.3 - (a) Find the intervals of increase or decrease....Ch. 4.3 - (a) Find the intervals of increase or decrease....Ch. 4.3 - (a) Find the intervals of increase or decrease....Ch. 4.3 - (a) Find the intervals of increase or decrease....Ch. 4.3 - (a) Find the intervals of increase or decrease....Ch. 4.3 - (a) Find the intervals of increase or decrease....Ch. 4.3 - (a) Find the intervals of increase or decrease....Ch. 4.3 - (a) Find the intervals of increase or decrease....Ch. 4.3 - (a) Find the intervals of increase or decrease....Ch. 4.3 - (a) Find the intervals of increase or decrease....Ch. 4.3 - (a) Find the intervals of increase or decrease....Ch. 4.3 - (a) Find the vertical and horizontal asymptotes....Ch. 4.3 - (a) Find the vertical and horizontal asymptotes....Ch. 4.3 - Prob. 51ECh. 4.3 - (a) Find the vertical and horizontal asymptotes....Ch. 4.3 - Prob. 53ECh. 4.3 - Prob. 54ECh. 4.3 - Prob. 55ECh. 4.3 - Prob. 56ECh. 4.3 - Prob. 57ECh. 4.3 - Prob. 58ECh. 4.3 - Prob. 59ECh. 4.3 - Prob. 60ECh. 4.3 - Prob. 61ECh. 4.3 - Prob. 62ECh. 4.3 - In an episode of The Simpsons television show,...Ch. 4.3 - Prob. 67ECh. 4.3 - Prob. 68ECh. 4.3 - Prob. 69ECh. 4.3 - Prob. 70ECh. 4.3 - Prob. 71ECh. 4.3 - Prob. 72ECh. 4.3 - Find a cubic function f(x) = ax3 + bx2 + cx + d...Ch. 4.3 - Prob. 74ECh. 4.3 - Prob. 75ECh. 4.3 - Prob. 76ECh. 4.3 - Prob. 77ECh. 4.3 - Prob. 78ECh. 4.3 - Prob. 79ECh. 4.3 - Prob. 80ECh. 4.3 - Prob. 81ECh. 4.3 - Prob. 82ECh. 4.3 - Prob. 83ECh. 4.3 - Prob. 84ECh. 4.3 - Prob. 85ECh. 4.3 - Prob. 86ECh. 4.3 - Prob. 87ECh. 4.3 - Prob. 88ECh. 4.3 - Prob. 89ECh. 4.3 - Prob. 90ECh. 4.3 - Prob. 92ECh. 4.3 - Prob. 93ECh. 4.4 - Given that...Ch. 4.4 - Prob. 2ECh. 4.4 - Prob. 3ECh. 4.4 - Prob. 4ECh. 4.4 - Use the graphs of f and g and their tangent lines...Ch. 4.4 - Use the graphs of f and g and their tangent lines...Ch. 4.4 - The graph of a function f and its tangent line at...Ch. 4.4 - Prob. 8ECh. 4.4 - Prob. 9ECh. 4.4 - Prob. 10ECh. 4.4 - Prob. 11ECh. 4.4 - Prob. 12ECh. 4.4 - Prob. 13ECh. 4.4 - Prob. 14ECh. 4.4 - Prob. 15ECh. 4.4 - Prob. 16ECh. 4.4 - Prob. 17ECh. 4.4 - Prob. 18ECh. 4.4 - Prob. 19ECh. 4.4 - Prob. 20ECh. 4.4 - Find the limit. Use lHospitals Rule where...Ch. 4.4 - Prob. 22ECh. 4.4 - Prob. 23ECh. 4.4 - Prob. 24ECh. 4.4 - Find the limit. Use lHospitals Rule where...Ch. 4.4 - Find the limit. Use lHospitals Rule where...Ch. 4.4 - Prob. 27ECh. 4.4 - Prob. 28ECh. 4.4 - Prob. 29ECh. 4.4 - Prob. 30ECh. 4.4 - Prob. 31ECh. 4.4 - Prob. 32ECh. 4.4 - Prob. 33ECh. 4.4 - Prob. 34ECh. 4.4 - Prob. 35ECh. 4.4 - Prob. 36ECh. 4.4 - Prob. 37ECh. 4.4 - Prob. 38ECh. 4.4 - Prob. 39ECh. 4.4 - Prob. 40ECh. 4.4 - Prob. 41ECh. 4.4 - Prob. 42ECh. 4.4 - Prob. 43ECh. 4.4 - Prob. 44ECh. 4.4 - Prob. 45ECh. 4.4 - Prob. 46ECh. 4.4 - Prob. 47ECh. 4.4 - Prob. 48ECh. 4.4 - Prob. 49ECh. 4.4 - Prob. 50ECh. 4.4 - Prob. 51ECh. 4.4 - Find the limit. Use lHospitals Rule where...Ch. 4.4 - Prob. 53ECh. 4.4 - Find the limit. Use lHospitals Rule where...Ch. 4.4 - Find the limit. Use lHospitals Rule where...Ch. 4.4 - Find the limit. Use lHospitals Rule where...Ch. 4.4 - Find the limit. Use lHospitals Rule where...Ch. 4.4 - Find the limit. Use lHospitals Rule where...Ch. 4.4 - Prob. 59ECh. 4.4 - Prob. 60ECh. 4.4 - Prob. 61ECh. 4.4 - Prob. 62ECh. 4.4 - Prob. 63ECh. 4.4 - Prob. 64ECh. 4.4 - Prob. 65ECh. 4.4 - Prob. 66ECh. 4.4 - Prob. 67ECh. 4.4 - Prob. 68ECh. 4.4 - Prob. 69ECh. 4.4 - Prob. 70ECh. 4.4 - Prob. 71ECh. 4.4 - Prob. 72ECh. 4.4 - Prob. 73ECh. 4.4 - Prob. 74ECh. 4.4 - Prob. 75ECh. 4.4 - Prob. 76ECh. 4.4 - Prob. 77ECh. 4.4 - Prob. 78ECh. 4.4 - If an initial amount A0 of money is invested at an...Ch. 4.4 - Prob. 80ECh. 4.4 - Prob. 81ECh. 4.4 - Prob. 82ECh. 4.4 - Prob. 83ECh. 4.4 - Prob. 84ECh. 4.4 - Prob. 85ECh. 4.4 - Prob. 86ECh. 4.4 - Prob. 87ECh. 4.4 - Prob. 88ECh. 4.4 - Prob. 89ECh. 4.4 - Prob. 90ECh. 4.4 - Prob. 91ECh. 4.4 - Prob. 92ECh. 4.5 - Use the guidelines of this section to sketch the...Ch. 4.5 - Prob. 2ECh. 4.5 - Prob. 3ECh. 4.5 - Prob. 4ECh. 4.5 - Prob. 5ECh. 4.5 - Prob. 6ECh. 4.5 - Prob. 7ECh. 4.5 - Prob. 8ECh. 4.5 - Prob. 9ECh. 4.5 - Use the guidelines of this section to sketch the...Ch. 4.5 - Prob. 11ECh. 4.5 - Use the guidelines of this section to sketch the...Ch. 4.5 - Prob. 13ECh. 4.5 - Prob. 14ECh. 4.5 - Prob. 15ECh. 4.5 - Prob. 16ECh. 4.5 - Prob. 17ECh. 4.5 - Prob. 18ECh. 4.5 - Prob. 19ECh. 4.5 - Prob. 20ECh. 4.5 - Prob. 21ECh. 4.5 - Prob. 22ECh. 4.5 - Prob. 23ECh. 4.5 - Prob. 24ECh. 4.5 - Prob. 25ECh. 4.5 - Prob. 26ECh. 4.5 - Prob. 27ECh. 4.5 - Prob. 28ECh. 4.5 - Prob. 29ECh. 4.5 - Prob. 30ECh. 4.5 - Prob. 31ECh. 4.5 - Prob. 32ECh. 4.5 - Prob. 33ECh. 4.5 - Prob. 34ECh. 4.5 - Prob. 35ECh. 4.5 - Prob. 36ECh. 4.5 - Prob. 37ECh. 4.5 - Prob. 38ECh. 4.5 - Prob. 39ECh. 4.5 - Prob. 40ECh. 4.5 - Prob. 41ECh. 4.5 - Prob. 42ECh. 4.5 - Prob. 43ECh. 4.5 - Prob. 44ECh. 4.5 - Prob. 45ECh. 4.5 - Prob. 46ECh. 4.5 - Prob. 47ECh. 4.5 - Prob. 48ECh. 4.5 - Prob. 49ECh. 4.5 - Prob. 50ECh. 4.5 - Prob. 51ECh. 4.5 - Prob. 52ECh. 4.5 - Prob. 53ECh. 4.5 - Prob. 54ECh. 4.5 - Prob. 55ECh. 4.5 - Prob. 56ECh. 4.5 - Prob. 57ECh. 4.5 - A model for the concentration at time t of a drug...Ch. 4.5 - Prob. 59ECh. 4.5 - Prob. 60ECh. 4.5 - Prob. 61ECh. 4.5 - Prob. 62ECh. 4.5 - Prob. 63ECh. 4.5 - Prob. 64ECh. 4.5 - Use the guidelines of this section to sketch the...Ch. 4.5 - Prob. 66ECh. 4.5 - Prob. 67ECh. 4.5 - Prob. 68ECh. 4.5 - Prob. 69ECh. 4.5 - Use the guidelines of this section to sketch the...Ch. 4.5 - Prob. 71ECh. 4.5 - Prob. 72ECh. 4.5 - Prob. 73ECh. 4.5 - Prob. 74ECh. 4.5 - Prob. 75ECh. 4.5 - Prob. 76ECh. 4.6 - Prob. 1ECh. 4.6 - Prob. 2ECh. 4.6 - Prob. 3ECh. 4.6 - Prob. 4ECh. 4.6 - Prob. 5ECh. 4.6 - Prob. 6ECh. 4.6 - Prob. 9ECh. 4.6 - Prob. 10ECh. 4.6 - Prob. 13ECh. 4.6 - Prob. 14ECh. 4.6 - Prob. 27ECh. 4.6 - Prob. 28ECh. 4.6 - Prob. 29ECh. 4.6 - Prob. 30ECh. 4.6 - Prob. 33ECh. 4.6 - Prob. 34ECh. 4.6 - Prob. 35ECh. 4.6 - Prob. 38ECh. 4.6 - Prob. 39ECh. 4.6 - Prob. 40ECh. 4.7 - Consider the following problem: Find two numbers...Ch. 4.7 - Find two numbers whose difference is 100 and whose...Ch. 4.7 - Prob. 3ECh. 4.7 - The sum of two positive numbers is 16. What is the...Ch. 4.7 - What is the maximum vertical distance between the...Ch. 4.7 - Prob. 6ECh. 4.7 - Prob. 7ECh. 4.7 - Prob. 8ECh. 4.7 - Prob. 9ECh. 4.7 - Prob. 10ECh. 4.7 - Prob. 11ECh. 4.7 - Prob. 12ECh. 4.7 - Prob. 13ECh. 4.7 - Prob. 14ECh. 4.7 - Prob. 15ECh. 4.7 - Prob. 16ECh. 4.7 - Prob. 17ECh. 4.7 - A farmer wants to fence in a rectangular plot of...Ch. 4.7 - Prob. 19ECh. 4.7 - Prob. 20ECh. 4.7 - Prob. 21ECh. 4.7 - Prob. 22ECh. 4.7 - Prob. 23ECh. 4.7 - Prob. 24ECh. 4.7 - Prob. 25ECh. 4.7 - Prob. 26ECh. 4.7 - Prob. 27ECh. 4.7 - Prob. 28ECh. 4.7 - Prob. 29ECh. 4.7 - Prob. 30ECh. 4.7 - Prob. 31ECh. 4.7 - Prob. 32ECh. 4.7 - Prob. 33ECh. 4.7 - A Norman window has the shape of a rectangle...Ch. 4.7 - Prob. 35ECh. 4.7 - A poster is to have an area of 180 in2 with 1-inch...Ch. 4.7 - Prob. 37ECh. 4.7 - Prob. 38ECh. 4.7 - If you are offered one slice from a round pizza...Ch. 4.7 - Prob. 40ECh. 4.7 - A cone-shaped drinking cup is made from a circular...Ch. 4.7 - Prob. 42ECh. 4.7 - Prob. 43ECh. 4.7 - Prob. 44ECh. 4.7 - Prob. 45ECh. 4.7 - For a fish swimming at a speed v relative to the...Ch. 4.7 - Prob. 47ECh. 4.7 - A boat leaves a dock at 2:00 pm and travels due...Ch. 4.7 - Prob. 49ECh. 4.7 - Prob. 50ECh. 4.7 - An oil refinery is located on the north bank of a...Ch. 4.7 - Prob. 52ECh. 4.7 - Prob. 53ECh. 4.7 - Prob. 54ECh. 4.7 - Prob. 55ECh. 4.7 - At which points on the curve y = 1 + 40x3 3x5...Ch. 4.7 - Prob. 57ECh. 4.7 - Prob. 58ECh. 4.7 - Prob. 59ECh. 4.7 - Prob. 60ECh. 4.7 - Prob. 61ECh. 4.7 - Prob. 62ECh. 4.7 - A retailer has been selling 1200 tablet computers...Ch. 4.7 - Prob. 64ECh. 4.7 - Prob. 65ECh. 4.7 - Prob. 66ECh. 4.7 - Prob. 67ECh. 4.7 - Prob. 68ECh. 4.7 - A point P needs to be located somewhere on the...Ch. 4.7 - The graph shows the fuel consumption c of a car...Ch. 4.7 - Prob. 71ECh. 4.7 - Prob. 72ECh. 4.7 - Prob. 73ECh. 4.7 - Prob. 74ECh. 4.7 - Prob. 75ECh. 4.7 - Prob. 76ECh. 4.7 - Where should the point P be chosen on the line...Ch. 4.7 - Prob. 78ECh. 4.7 - Find the maximum area of a rectangle that can be...Ch. 4.7 - The blood vascular system consists of blood...Ch. 4.7 - Ornithologists have determined that some species...Ch. 4.7 - Prob. 82ECh. 4.8 - The figure shows the graph of a function f....Ch. 4.8 - Prob. 2ECh. 4.8 - Prob. 3ECh. 4.8 - For each initial approximation, determine...Ch. 4.8 - Prob. 5ECh. 4.8 - Prob. 6ECh. 4.8 - Prob. 7ECh. 4.8 - Prob. 8ECh. 4.8 - Prob. 9ECh. 4.8 - Prob. 10ECh. 4.8 - Prob. 11ECh. 4.8 - Prob. 12ECh. 4.8 - Prob. 13ECh. 4.8 - Prob. 14ECh. 4.8 - Prob. 15ECh. 4.8 - Prob. 16ECh. 4.8 - Prob. 17ECh. 4.8 - Prob. 18ECh. 4.8 - Prob. 19ECh. 4.8 - Prob. 20ECh. 4.8 - Prob. 21ECh. 4.8 - Prob. 22ECh. 4.8 - Prob. 23ECh. 4.8 - Prob. 24ECh. 4.8 - Prob. 25ECh. 4.8 - Prob. 26ECh. 4.8 - Prob. 27ECh. 4.8 - (a) Apply Newtons method to the equation x2 a = 0...Ch. 4.8 - Prob. 30ECh. 4.8 - Prob. 32ECh. 4.8 - Prob. 33ECh. 4.8 - If f(x)={xifx0xifx0 then the root of the equation...Ch. 4.8 - Prob. 35ECh. 4.8 - Prob. 36ECh. 4.8 - Prob. 37ECh. 4.8 - Use Newtons method to find the coordinates,...Ch. 4.8 - Prob. 40ECh. 4.8 - Prob. 41ECh. 4.8 - Prob. 42ECh. 4.9 - Find the most general antiderivative of the...Ch. 4.9 - Prob. 2ECh. 4.9 - Prob. 3ECh. 4.9 - Prob. 4ECh. 4.9 - Prob. 5ECh. 4.9 - Prob. 6ECh. 4.9 - Prob. 7ECh. 4.9 - Prob. 8ECh. 4.9 - Prob. 9ECh. 4.9 - Prob. 10ECh. 4.9 - Prob. 11ECh. 4.9 - Prob. 12ECh. 4.9 - Prob. 13ECh. 4.9 - Prob. 14ECh. 4.9 - Prob. 15ECh. 4.9 - Find the most general antiderivative of the...Ch. 4.9 - Prob. 17ECh. 4.9 - Prob. 18ECh. 4.9 - Find the most general antiderivative of the...Ch. 4.9 - Prob. 20ECh. 4.9 - Prob. 21ECh. 4.9 - Prob. 22ECh. 4.9 - Prob. 25ECh. 4.9 - Prob. 26ECh. 4.9 - Prob. 27ECh. 4.9 - Prob. 28ECh. 4.9 - Prob. 29ECh. 4.9 - Prob. 30ECh. 4.9 - Find f. f(x)=1+3x, f(4) = 25Ch. 4.9 - Prob. 32ECh. 4.9 - Prob. 33ECh. 4.9 - Find f. f(t) = t + 1/t3, t 0, f(1) = 6Ch. 4.9 - Prob. 35ECh. 4.9 - Prob. 36ECh. 4.9 - Prob. 37ECh. 4.9 - Prob. 38ECh. 4.9 - Prob. 39ECh. 4.9 - Prob. 40ECh. 4.9 - Prob. 41ECh. 4.9 - Prob. 42ECh. 4.9 - Prob. 43ECh. 4.9 - Find f. f(x) = x3 + sinh x, f(0) = 1, f(2) = 2.6Ch. 4.9 - Prob. 45ECh. 4.9 - Prob. 46ECh. 4.9 - Prob. 47ECh. 4.9 - Prob. 48ECh. 4.9 - Prob. 49ECh. 4.9 - Prob. 50ECh. 4.9 - Prob. 51ECh. 4.9 - The graph of a function f is shown. Which graph is...Ch. 4.9 - Prob. 53ECh. 4.9 - The graph of the velocity function of a particle...Ch. 4.9 - Prob. 55ECh. 4.9 - Prob. 56ECh. 4.9 - Prob. 57ECh. 4.9 - Prob. 58ECh. 4.9 - Prob. 59ECh. 4.9 - Prob. 60ECh. 4.9 - Prob. 61ECh. 4.9 - Prob. 62ECh. 4.9 - Prob. 63ECh. 4.9 - Prob. 64ECh. 4.9 - Prob. 65ECh. 4.9 - Prob. 66ECh. 4.9 - Prob. 67ECh. 4.9 - Two balls are thrown upward from the edge of the...Ch. 4.9 - Prob. 69ECh. 4.9 - If a diver of mass m stands at the end of a diving...Ch. 4.9 - Prob. 71ECh. 4.9 - Prob. 72ECh. 4.9 - Prob. 73ECh. 4.9 - Prob. 74ECh. 4.9 - Prob. 75ECh. 4.9 - Prob. 76ECh. 4.9 - A car is traveling at 100 km/h when the driver...Ch. 4.9 - A high-speed bullet train accelerates and...Ch. 4 - Explain the difference between an absolute maximum...Ch. 4 - Prob. 2RCCCh. 4 - Prob. 3RCCCh. 4 - Prob. 4RCCCh. 4 - Prob. 5RCCCh. 4 - Prob. 6RCCCh. 4 - Prob. 7RCCCh. 4 - Prob. 8RCCCh. 4 - Prob. 9RCCCh. 4 - Prob. 10RCCCh. 4 - Prob. 11RCCCh. 4 - Prob. 1RQCh. 4 - Prob. 2RQCh. 4 - If f is continuous on (a, b), then f attains an...Ch. 4 - Prob. 4RQCh. 4 - Prob. 5RQCh. 4 - If f(2) = 0, then (2, f(2)) is an inflection point...Ch. 4 - Prob. 7RQCh. 4 - Prob. 8RQCh. 4 - Prob. 9RQCh. 4 - Prob. 10RQCh. 4 - Prob. 11RQCh. 4 - Prob. 12RQCh. 4 - Prob. 13RQCh. 4 - If f and g are positive increasing functions on an...Ch. 4 - Prob. 15RQCh. 4 - Prob. 16RQCh. 4 - Prob. 17RQCh. 4 - Prob. 18RQCh. 4 - If f(x) exists and is nonzero for all x, then f(1)...Ch. 4 - Prob. 20RQCh. 4 - Prob. 21RQCh. 4 - Prob. 1RECh. 4 - Prob. 2RECh. 4 - Prob. 3RECh. 4 - Prob. 4RECh. 4 - Prob. 5RECh. 4 - Prob. 6RECh. 4 - Evaluate the limit. limx0ex1tanxCh. 4 - Prob. 8RECh. 4 - Prob. 9RECh. 4 - Prob. 10RECh. 4 - Prob. 11RECh. 4 - Prob. 12RECh. 4 - Prob. 13RECh. 4 - Prob. 14RECh. 4 - Prob. 15RECh. 4 - Prob. 16RECh. 4 - Prob. 17RECh. 4 - Prob. 18RECh. 4 - Prob. 19RECh. 4 - Prob. 20RECh. 4 - Prob. 21RECh. 4 - Prob. 22RECh. 4 - Prob. 23RECh. 4 - Prob. 24RECh. 4 - Prob. 25RECh. 4 - Prob. 26RECh. 4 - Prob. 27RECh. 4 - Prob. 28RECh. 4 - Prob. 29RECh. 4 - Prob. 30RECh. 4 - Prob. 31RECh. 4 - Prob. 32RECh. 4 - Prob. 33RECh. 4 - Prob. 34RECh. 4 - Prob. 35RECh. 4 - Prob. 36RECh. 4 - Prob. 37RECh. 4 - Prob. 38RECh. 4 - Prob. 39RECh. 4 - Prob. 43RECh. 4 - Prob. 44RECh. 4 - Prob. 45RECh. 4 - Prob. 46RECh. 4 - By applying the Mean Value Theorem to the function...Ch. 4 - Prob. 48RECh. 4 - Prob. 49RECh. 4 - Prob. 50RECh. 4 - Prob. 51RECh. 4 - Prob. 52RECh. 4 - Prob. 53RECh. 4 - Prob. 54RECh. 4 - Prob. 55RECh. 4 - Prob. 56RECh. 4 - Prob. 57RECh. 4 - Prob. 58RECh. 4 - A hockey team plays in an arena with a seating...Ch. 4 - Prob. 60RECh. 4 - Prob. 61RECh. 4 - Prob. 62RECh. 4 - Prob. 63RECh. 4 - Prob. 64RECh. 4 - Prob. 65RECh. 4 - Prob. 66RECh. 4 - Prob. 67RECh. 4 - Prob. 68RECh. 4 - Prob. 69RECh. 4 - Prob. 70RECh. 4 - Prob. 71RECh. 4 - Prob. 72RECh. 4 - Prob. 73RECh. 4 - Prob. 74RECh. 4 - Prob. 75RECh. 4 - Prob. 76RECh. 4 - Prob. 77RECh. 4 - Prob. 78RECh. 4 - Prob. 79RECh. 4 - If a projectile is fired with an initial velocity...Ch. 4 - Prob. 81RECh. 4 - If a metal ball with mass m is projected in water...Ch. 4 - Prob. 83RECh. 4 - Prob. 84RECh. 4 - Prob. 85RECh. 4 - Prob. 86RECh. 4 - Prob. 1PCh. 4 - Prob. 2PCh. 4 - Prob. 3PCh. 4 - Prob. 4PCh. 4 - Prob. 5PCh. 4 - Prob. 6PCh. 4 - If a, b, c, and d are constants such that...Ch. 4 - Prob. 8PCh. 4 - Prob. 9PCh. 4 - Prob. 10PCh. 4 - Prob. 11PCh. 4 - For what values of c does the curve y = cx3 + ex...Ch. 4 - Prob. 13PCh. 4 - Prob. 14PCh. 4 - Prob. 15PCh. 4 - Prob. 16PCh. 4 - Prob. 17PCh. 4 - Prob. 18PCh. 4 - Prob. 19PCh. 4 - An arc PQ of a circle subtends a central angle as...Ch. 4 - Prob. 21PCh. 4 - Prob. 22PCh. 4 - Prob. 23PCh. 4 - Prob. 25PCh. 4 - A hemispherical bubble is placed on a spherical...
Knowledge Booster
Learn more about
Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, calculus and related others by exploring similar questions and additional content below.Similar questions
- If a functionfis increasing on (a,b) and decreasing on (b,c) , then what can be said about the local extremum offon (a,c) ?arrow_forwardGiven the function f(x) = sqrt(3x), determine the slope of the tangent line of f at x=6 using the limit shown below. You do not have to simplify your answer. Limx->6arrow_forwardUse the definition mtan=limh→0f(a+h)−f(a)h a. to find the slope of the line tangent to the graph of f at P. b. Determine an equation of the tangent line at P. f(x)=6x+2, P(0,2)arrow_forward
arrow_back_ios
arrow_forward_ios
Recommended textbooks for you

Limits and Continuity; Author: The Organic Chemistry Tutor;https://www.youtube.com/watch?v=9brk313DjV8;License: Standard YouTube License, CC-BY