
Elementary Geometry For College Students, 7e
7th Edition
ISBN: 9781337614085
Author: Alexander, Daniel C.; Koeberlein, Geralyn M.
Publisher: Cengage,
expand_more
expand_more
format_list_bulleted
Textbook Question
Chapter 5.5, Problem 21E
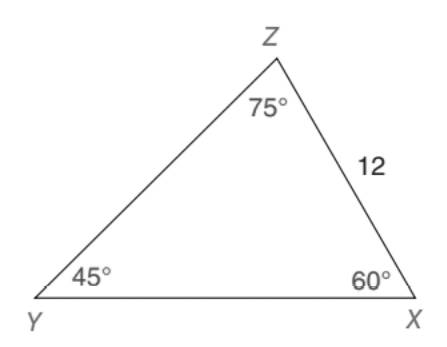
| Given: |
as shown in the drawing |
| Find: |
|
| (HINT: | Compare this drawing to the one for Exercise 20.) |
Expert Solution & Answer
Want to see the full answer?
Check out a sample textbook solution
Chapter 5 Solutions
Elementary Geometry For College Students, 7e
Ch. 5.1 - In Exercises 1 to 4, give the ratios in simplified...Ch. 5.1 - In Exercises 1 to 4, give the ratios in simplified...Ch. 5.1 - In Exercises 1 to 4, give the ratios in simplified...Ch. 5.1 - In Exercises 1 to 4, give the ratios in simplified...Ch. 5.1 - In Exercises 5 to 14, find the value of x in each...Ch. 5.1 - In Exercises 5 to 14, find the value of x in each...Ch. 5.1 - In Exercises 5 to 14, find the value of x in each...Ch. 5.1 - In Exercises 5 to 14, find the value of x in each...Ch. 5.1 - In Exercises 5 to 14, find the value of x in each...Ch. 5.1 - In Exercises 5 to 14, find the value of x in each...
Ch. 5.1 - In Exercises 5 to 14, find the value of x in each...Ch. 5.1 - In Exercises 5 to 14, find the value of x in each...Ch. 5.1 - In Exercises 5 to 14, find the value of x in each...Ch. 5.1 - In Exercises 5 to 14, find the value of x in each...Ch. 5.1 - Sarah ran the 300-m hurdles in 47.7 sec. In meters...Ch. 5.1 - Fran has been hired to sew the dance troupes...Ch. 5.1 - In Exercises 17 to 22, use proportions to solve...Ch. 5.1 - In Exercises 17 to 22, use proportions to solve...Ch. 5.1 - In Exercises 17 to 22, use proportions to solve...Ch. 5.1 - In Exercises 17 to 22, use proportions to solve...Ch. 5.1 - In Exercises 17 to 22, use proportions to solve...Ch. 5.1 - In Exercises 17 to 22, use proportions to solve...Ch. 5.1 - The salaries of a secretary, a salesperson, and a...Ch. 5.1 - The salaries of a school cook, custodian, and bus...Ch. 5.1 - If the measures of the angles of a quadrilateral...Ch. 5.1 - If the measures of the angles of a quadrilateral...Ch. 5.1 - Prob. 27ECh. 5.1 - Prob. 28ECh. 5.1 - If 1 in. equals 2.54 cm, use a proportion to...Ch. 5.1 - If 1 kg equals 2.2 lb, use a proportion to convert...Ch. 5.1 - For the quadrilaterals shown, MNWX=NPXY=PQYZ=MQWZ....Ch. 5.1 - Prob. 32ECh. 5.1 - Two numbers a and b are in the ratio 3:4. If the...Ch. 5.1 - Two numbers a and b are in the ratio 2:3. If both...Ch. 5.1 - If the ratio of the measure of the complement of...Ch. 5.1 - If the ratio of the measure of the complement of...Ch. 5.1 - On a blueprint, a 1-in. scale corresponds to 3 ft....Ch. 5.1 - To find the golden ratio see the Discover activity...Ch. 5.1 - Find a the exact length of an ideal rectangle with...Ch. 5.1 - Prove: If ab=cd where a, b, c and d are nonzero,...Ch. 5.1 - Prob. 41ECh. 5.1 - In the figure, assume that a 0. Prove that...Ch. 5.1 - In the figure, assume that a 0. Prove that...Ch. 5.2 - a What is true of any pair of corresponding angles...Ch. 5.2 - a Are any two quadrilaterals similar? b Are any...Ch. 5.2 - a Are any two regular pentagons similar? b Are any...Ch. 5.2 - a Are any two equilateral hexagons similar? b Are...Ch. 5.2 - In Exercises 5 and 6, refer to the drawing. a...Ch. 5.2 - In Exercises 5 and 6, refer to the drawing. a If...Ch. 5.2 - Prob. 7ECh. 5.2 - Given that rectangle ABCE is similar to rectangle...Ch. 5.2 - Given: MNPQRS,mM=56,mR=82,MN=9,QR=6,RS=7,MP=12...Ch. 5.2 - Given: ABCPRC,mA=67,PC=5,CR=12,PR=13,AB=26 Find: a...Ch. 5.2 - a Does the similarity relationship have a...Ch. 5.2 - Using the names of property from Exercise 11,...Ch. 5.2 - If the drawing, HJKFGK. If HK=6,KF=8, and HJ=4,...Ch. 5.2 - If the drawing, HJKFGK. If HK=6,KF=8, and FG=5,...Ch. 5.2 - Quadrilateral ABCD quadrilateral HJKL. If mA=55,...Ch. 5.2 - Quadrilateral ABCD quadrilateral HJKL. If...Ch. 5.2 - Quadrilateral ABCD quadrilateral HJKL. If...Ch. 5.2 - Quadrilateral ABCD quadrilateral HJKL. If...Ch. 5.2 - Quadrilateral ABCD quadrilateral HJKL. If...Ch. 5.2 - Quadrilateral ABCD quadrilateral HJKL. If...Ch. 5.2 - In Exercises 21 to 24, ADEABC. Given:...Ch. 5.2 - In Exercises 21 to 24, ADEABC. Given:...Ch. 5.2 - In Exercises 21 to 24, ADEABC. Given:...Ch. 5.2 - In Exercises 21 to 24, ADEABC. Given:...Ch. 5.2 - Pentagon ABCDE pentagon GHJKL not shown, AB=6, and...Ch. 5.2 - Quadrilateral MNPQ quadrilateral WXYZ not shown,...Ch. 5.2 - Prob. 27ECh. 5.2 - A technical drawing shows the 312 ft lengths of...Ch. 5.2 - In Exercises 29 to 32, use the fact that triangles...Ch. 5.2 - In Exercise 29 to 32, use the fact that triangles...Ch. 5.2 - In Exercise 29 to 32, use the fact that triangles...Ch. 5.2 - In Exercise 29 to 32, use the fact that triangles...Ch. 5.2 - In the drawing, ABDCEF with transversals l and m....Ch. 5.2 - In the drawing, ABDCEF. Suppose that transversals...Ch. 5.2 - Prob. 35ECh. 5.2 - Given RST, a second triangle (UVW) is constructed...Ch. 5.2 - Henry watches his 32 inch diagonal LCD television...Ch. 5.2 - Prob. 38ECh. 5.2 - Prob. 39ECh. 5.2 - For Exercises 39 to 40, use intuition to from a...Ch. 5.3 - What is the acronym that is used to represent each...Ch. 5.3 - Classify as true or false. a Any two rectangles...Ch. 5.3 - Classify as true or false: a If the vertex angles...Ch. 5.3 - Classify as true or false: a If the midpoints of...Ch. 5.3 - In Exercises 5 to 8, name the method...Ch. 5.3 - In Exercises 5 to 8, name the method...Ch. 5.3 - In Exercises 5 to 8, name the method...Ch. 5.3 - In Exercises 5 to 8, name the method...Ch. 5.3 - In Exercises 9 to 12, name the method that...Ch. 5.3 - In Exercises 9 to 12, name the method that...Ch. 5.3 - In Exercises 9 to 12, name the method that...Ch. 5.3 - In Exercises 9 to 12, name the method that...Ch. 5.3 - In Exercises 13 to 16, provide the missing...Ch. 5.3 - In Exercises 13 to 16, provide the missing...Ch. 5.3 - In Exercises 13 to 16, provide the missing...Ch. 5.3 - In Exercises 13 to 16, provide the missing...Ch. 5.3 - In Exercises 17 to 24, complete each proof. Given:...Ch. 5.3 - In Exercises 17 to 24, complete each proof. Given:...Ch. 5.3 - Prob. 19ECh. 5.3 - In Exercises 17 to 24, complete each proof. Given:...Ch. 5.3 - In Exercises 17 to 24, complete each proof. Given:...Ch. 5.3 - In Exercises 17 to 24, complete each proof. Given:...Ch. 5.3 - In Exercises 17 to 24, complete each proof. Given:...Ch. 5.3 - Prob. 24ECh. 5.3 - In Exercises 25 to 28, ABCDBE Exercises 25-28...Ch. 5.3 - In Exercises 25 to 28, ABCDBE Exercises 25-28...Ch. 5.3 - In Exercises 25 to 28, ABCDBE Exercises 25-28...Ch. 5.3 - In Exercises 25 to 28, ABCDBE Exercises 25-28...Ch. 5.3 - CDECBA with CDEB. If CD=10,DA=8 and CE=6, find EB....Ch. 5.3 - CDECBA with CDEB. If CD=10,CA=16 and EB=12, find...Ch. 5.3 - ABFCBD with obtuse angles at vertices D and F as...Ch. 5.3 - ABFCBD with obtuse angles at vertices D and F as...Ch. 5.3 - In Exercise 33, provide a two-column proof....Ch. 5.3 - In Exercise 34, provide a paragraph proof. Given:...Ch. 5.3 - Use a two-column proof to prove the following...Ch. 5.3 - Prob. 36ECh. 5.3 - Use the result of Exercise 13 to do the following...Ch. 5.3 - Use the result of Exercise 13 to do the following...Ch. 5.3 - The distance across a pond is to be measured...Ch. 5.3 - In the figure, ABCADB. Find AB if AD=2 and DC=6.Ch. 5.3 - Prove that the altitude drawn to the hypotenuse of...Ch. 5.3 - Prove that the line segment joining the midpoints...Ch. 5.3 - Prob. 43ECh. 5.4 - By naming the vertices in order, state three...Ch. 5.4 - Use theorem 5.4.2 to form a proportion in which SV...Ch. 5.4 - Use theorem 5.4.3 to form a proportion in which RS...Ch. 5.4 - Use theorem 5.4.3 to form a proportion in which TS...Ch. 5.4 - Use theorem 5.4.2 to find RV if SV=6 and VT=8....Ch. 5.4 - Prob. 6ECh. 5.4 - Find the length of DF if: a DE=8 and EF=6. b DE=5...Ch. 5.4 - Find the length of DE if: a DF=13 and EF=5. b...Ch. 5.4 - Find EF if: a DF=17 and DE=15. b DF=12 and DE=82....Ch. 5.4 - Find DF if: a DE=12 and EF=5 b DF=12 and EF=6....Ch. 5.4 - Determine whether each triple (a,b,c) is a...Ch. 5.4 - Prob. 12ECh. 5.4 - Prob. 13ECh. 5.4 - Determine the type of triangle represented if the...Ch. 5.4 - A guy wire 25 ft long supports an antenna at a...Ch. 5.4 - A strong wind holds a kite 30 ft above the earth...Ch. 5.4 - A boat is 6 m below the level of a pier and 12 m...Ch. 5.4 - A hot-air balloon is held in place by the ground...Ch. 5.4 - A drawbridge that is 104 ft in length is raised at...Ch. 5.4 - A drawbridge that is 136 ft in length is raised at...Ch. 5.4 - A rectangle has a width of 16 cm and a diagonal of...Ch. 5.4 - A right triangle has legs of lengths x and 2x2 and...Ch. 5.4 - A rectangle has base length x3, altitude length...Ch. 5.4 - The diagonals of a rhombus measure 6 m and 8 m....Ch. 5.4 - Each side of a rhombus measure 12 in. If one...Ch. 5.4 - An isosceles right triangle has a hypotenuse of...Ch. 5.4 - Prob. 27ECh. 5.4 - In right ABC with right C, AB=10 and BC=8. Find...Ch. 5.4 - Prob. 29ECh. 5.4 - Prob. 30ECh. 5.4 - Find the length of the altitude to the 26-in. side...Ch. 5.4 - Prob. 32ECh. 5.4 - In quadrilateral RSTU, RSST and UT diagonal RT. If...Ch. 5.4 - Prob. 34ECh. 5.4 - If a=p2q2,b=2pq and c=p2+q2, show that c2=a2+b2.Ch. 5.4 - Prob. 36ECh. 5.4 - Prob. 37ECh. 5.4 - When the rectangle in the accompanying drawing...Ch. 5.4 - A, C and F are three of the vertices of the cube...Ch. 5.4 - Prob. 40ECh. 5.4 - In the figure, square RSTV has its vertices on the...Ch. 5.4 - Prove that if (a,b,c) is a Pythagorean triple and...Ch. 5.4 - Use Figure 5.19 to prove Theorem 5.4.2. Theorem...Ch. 5.4 - Use Figures 5.20 and 5.21 to prove Lemma 5.4.3....Ch. 5.4 - Prob. 45ECh. 5.5 - For the 45-45-90 triangle shown, suppose that...Ch. 5.5 - For the 45-45-90 triangle shown, suppose that...Ch. 5.5 - For the 30-60-90 triangle shown, suppose that...Ch. 5.5 - For the 30-60-90 triangle shown, suppose that...Ch. 5.5 - In Exercises 5 to 22, find the missing lengths....Ch. 5.5 - In Exercises 5 to 22, find the missing lengths....Ch. 5.5 - In Exercises 5 to 22, find the missing lengths....Ch. 5.5 - In Exercises 5 to 22, find the missing lengths....Ch. 5.5 - In Exercises 5 to 22, find the missing lengths....Ch. 5.5 - In Exercises 5 to 22, find the missing lengths....Ch. 5.5 - In Exercises 5 to 22, find the missing lengths....Ch. 5.5 - In Exercises 5 to 22, find the missing lengths....Ch. 5.5 - In Exercises 5 to 22, find the missing lengths....Ch. 5.5 - In Exercises 5 to 22, find the missing lengths....Ch. 5.5 - Prob. 15ECh. 5.5 - Prob. 16ECh. 5.5 - Prob. 17ECh. 5.5 - In Exercises 15 to 19, create drawings as needed....Ch. 5.5 - In Exercises15 to 19, create drawing as needed....Ch. 5.5 - Given: NQM with angles as shown in the drawing...Ch. 5.5 - Given: XYZ with angles as shown in the drawing...Ch. 5.5 - Given: Rhombus ABCD not shown in which diagonals...Ch. 5.5 - Prob. 23ECh. 5.5 - To unload groceries from a delivery truck at the...Ch. 5.5 - A jogger runs along two sides of an open...Ch. 5.5 - Prob. 26ECh. 5.5 - Prob. 27ECh. 5.5 - In Exercises 27 to 33, give both exact solutions...Ch. 5.5 - Prob. 29ECh. 5.5 - Prob. 30ECh. 5.5 - In Exercises 27 to 33, give both exact solutions...Ch. 5.5 - In Exercises 27 to 33, give both exact solutions...Ch. 5.5 - In Exercises 27 to 33, give both exact solutions...Ch. 5.5 - Note: Exercises preceded by an asterisk are of a...Ch. 5.5 - In regular hexagon ABCDEF, AB=6 inches. Find the...Ch. 5.5 - In regular hexagon ABCDEF, the length of AB is x...Ch. 5.5 - In right triangle XYZ, XY=3 and YZ=4. If V is the...Ch. 5.5 - Diagonal EC separates pentagon ABCDE into square...Ch. 5.5 - For equilateral RST, RT=6. Squares and triangles...Ch. 5.6 - Note: Exercises preceded by an asterisk are of a...Ch. 5.6 - Prob. 2ECh. 5.6 - Given that ABEF=BCFG=CDGH, are the following...Ch. 5.6 - Given that XYTS, are the following proportion...Ch. 5.6 - Given: l1l2l3l4,AB=5,BC=4,CD=3,EH=10 Find:...Ch. 5.6 - Given: l1l2l3l4,AB=7,BC=5,CD=4,EF=6 Find: FG,GH,EHCh. 5.6 - Given: l1l2l3,AB=4,BC=5,DE=x,EF=12x Find: x,DE,EFCh. 5.6 - Given: l1l2l3,AB=5,BC=x,DE=x2,EF=7 Find: x,BC,DECh. 5.6 - Given: DEBC,AD=5,DB=12,AE=7 Find: ECCh. 5.6 - Given: DEBC,AD=6,DB=10,AC=20 Find: ECCh. 5.6 - Prob. 11ECh. 5.6 - Given: DEBC,AD=5,DB=a+3,AE=a+1,EC=3(a1) Find:...Ch. 5.6 - Given: RW bisects SRT Do the following equalities...Ch. 5.6 - Given: RW bisects SRT Do the following equalities...Ch. 5.6 - Given: UT bisects WUV,WU=8,UV=12,WT=6 Find: TVCh. 5.6 - Given: UT bisects WUV,WU=9,UV=12,WV=9 Find: WTCh. 5.6 - Given: NQ bisects MNP,NP=MQ,QP=8,MN=12 Find: NPCh. 5.6 - Prob. 18ECh. 5.6 - Prob. 19ECh. 5.6 - Given: In ABC,AD bisects BAC AB=20 and AC=16 Find:...Ch. 5.6 - Prob. 21ECh. 5.6 - In ABC,mCAB=80,mACB=60,andABC=40. With the angle...Ch. 5.6 - In ABC,AC=5.3,BC=7.2 and BA=6.7. With angle...Ch. 5.6 - In right RST not shown with right S,RV bisects SRT...Ch. 5.6 - Given: RV bisects SRT, RS=x6,SV=3, RT=2x, and...Ch. 5.6 - Given: MR bisects NMP, MN=2x,NR=x, RP=x+1, and...Ch. 5.6 - Given point D in the interior of RST, which...Ch. 5.6 - In RST, suppose that RH,TG, and SK are medians....Ch. 5.6 - Prob. 29ECh. 5.6 - Prob. 30ECh. 5.6 - Prob. 31ECh. 5.6 - Given: RST, with XYRT and YZRS Prove: RXXS=ZTRZCh. 5.6 - Prob. 33ECh. 5.6 - Use Exercise 33 and the following drawing to...Ch. 5.6 - Use Theorem 5.6.3 to complete the proof of this...Ch. 5.6 - In right ABC,mB=30. Also, AB=123 and AD bisects...Ch. 5.6 - Prob. 37ECh. 5.6 - In right ABC with right C,AD bisects BAC. If AC=6...Ch. 5.6 - Given: ABC not shown is isosceles with...Ch. 5.6 - Given: RST with right RST; mR=30 and ST=6; RST is...Ch. 5.6 - Prob. 41ECh. 5.6 - Prob. 42ECh. 5.CR - Prob. 1CRCh. 5.CR - Prob. 2CRCh. 5.CR - Prob. 3CRCh. 5.CR - Prob. 4CRCh. 5.CR - Prob. 5CRCh. 5.CR - Prob. 6CRCh. 5.CR - Prob. 7CRCh. 5.CR - Find the values of x in each proportion: a x6=3x c...Ch. 5.CR - Use proportions to solve Review Exercises 9 to 11....Ch. 5.CR - Prob. 10CRCh. 5.CR - Prob. 11CRCh. 5.CR - The ratio of the measures of sides of a...Ch. 5.CR - Prob. 13CRCh. 5.CR - The length of the sides of a triangle are 6, 8 and...Ch. 5.CR - The ratio of the measure of the supplement of an...Ch. 5.CR - Prob. 16CRCh. 5.CR - Given: ABCD is a parallelogram. DB intersects AE...Ch. 5.CR - Prob. 18CRCh. 5.CR - Prob. 19CRCh. 5.CR - Prob. 20CRCh. 5.CR - Prob. 21CRCh. 5.CR - Prob. 22CRCh. 5.CR - Prob. 23CRCh. 5.CR - For Review Exercises 24 to 26, GJ bisects FGH...Ch. 5.CR - For Review Exercises 24 to 26, GJ bisects FGH...Ch. 5.CR - For Review Exercises 24 to 26, GJ bisects FGH...Ch. 5.CR - Given:...Ch. 5.CR - Prove that if a line bisects one side of a...Ch. 5.CR - Prove that the diagonals of a trapezoid divide...Ch. 5.CR - Given: ABCwithrightBACADBC...Ch. 5.CR - Given: ABCwithrightBACADBC...Ch. 5.CR - Prob. 32CRCh. 5.CR - Given:...Ch. 5.CR - Find the length of a diagonal of a square whose...Ch. 5.CR - Prob. 35CRCh. 5.CR - Find the length of a side of a rhombus whose...Ch. 5.CR - Find the length of an altitude of an equilateral...Ch. 5.CR - Prob. 38CRCh. 5.CR - The length of the three sides of a triangle are...Ch. 5.CR - Prob. 40CRCh. 5.CR - Prob. 41CRCh. 5.CR - Prob. 42CRCh. 5.CT - Reduce to its simplest form: a The ratio 12:20 b...Ch. 5.CT - Prob. 2CTCh. 5.CT - Prob. 3CTCh. 5.CT - Prob. 4CTCh. 5.CT - Prob. 5CTCh. 5.CT - In right triangle ABC,CD- is the altitude from C...Ch. 5.CT - Prob. 7CTCh. 5.CT - Given its lengths of sides, is RST a right...Ch. 5.CT - Prob. 9CTCh. 5.CT - In XYZ,XZ-YZ- and Z is a right angle. a Find XY if...Ch. 5.CT - In DEF,D is a right angle and m F=30. a Find DE if...Ch. 5.CT - Prob. 12CTCh. 5.CT - In MNP,NQ bisects MNP. If PN = 6, MN = 9, and MP =...Ch. 5.CT - Prob. 14CTCh. 5.CT - Prob. 15CTCh. 5.CT - Prob. 16CTCh. 5.CT - In Exercises 16 and 17, complete the statements...
Knowledge Booster
Learn more about
Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, geometry and related others by exploring similar questions and additional content below.Similar questions
- Given: Hole centerlines EFGH and MPKL. Determine the values of 1 through 15 for these values of 16 .arrow_forwardIn ABC, M is the midpoint of AB and N is the midpoint of AC. If MN= 3x-11 and BC= 4x24, find the value of x._arrow_forwardA tangent ET is constructed to circle Q from external point E. Which angle and which side of triangle QTE are largest? Which angle and which side are smallest?arrow_forward
- Given: Equiangular RST Prove: RV bisects SRT RVS is a rightarrow_forwardUse a two-column proof to prove the following theorem: The lengths of the corresponding altitudes of similar triangles have the same ratio as lengths of any pair of corresponding sides. Given: DEFMNP; DG and MQ are altitudes Prove: DGMQ=DEMNarrow_forwardWhat relationship, if any, exists between two angles a with equal measures? b that have the same vertex and a common side between them?arrow_forward
- 2. Consider XYZ triangles not shown a Which side is included by X and Y? b Which angle is included by sides XY and YZ?arrow_forwardDoes it follow from Exercise 30 that ADE is also congruent to CBE? What can you conclude regarding AE and CE in the drawing? What can you conclude regarding DEandBE?arrow_forwardConsider XYZ triangles not shown a Which side is included by X and Y?_ b Which angle is included by sides XY and YZ?_arrow_forward
arrow_back_ios
arrow_forward_ios
Recommended textbooks for you
 Elementary Geometry For College Students, 7eGeometryISBN:9781337614085Author:Alexander, Daniel C.; Koeberlein, Geralyn M.Publisher:Cengage,
Elementary Geometry For College Students, 7eGeometryISBN:9781337614085Author:Alexander, Daniel C.; Koeberlein, Geralyn M.Publisher:Cengage, Elementary Geometry for College StudentsGeometryISBN:9781285195698Author:Daniel C. Alexander, Geralyn M. KoeberleinPublisher:Cengage Learning
Elementary Geometry for College StudentsGeometryISBN:9781285195698Author:Daniel C. Alexander, Geralyn M. KoeberleinPublisher:Cengage Learning Mathematics For Machine TechnologyAdvanced MathISBN:9781337798310Author:Peterson, John.Publisher:Cengage Learning,
Mathematics For Machine TechnologyAdvanced MathISBN:9781337798310Author:Peterson, John.Publisher:Cengage Learning, Holt Mcdougal Larson Pre-algebra: Student Edition...AlgebraISBN:9780547587776Author:HOLT MCDOUGALPublisher:HOLT MCDOUGAL
Holt Mcdougal Larson Pre-algebra: Student Edition...AlgebraISBN:9780547587776Author:HOLT MCDOUGALPublisher:HOLT MCDOUGAL

Elementary Geometry For College Students, 7e
Geometry
ISBN:9781337614085
Author:Alexander, Daniel C.; Koeberlein, Geralyn M.
Publisher:Cengage,

Elementary Geometry for College Students
Geometry
ISBN:9781285195698
Author:Daniel C. Alexander, Geralyn M. Koeberlein
Publisher:Cengage Learning

Mathematics For Machine Technology
Advanced Math
ISBN:9781337798310
Author:Peterson, John.
Publisher:Cengage Learning,

Holt Mcdougal Larson Pre-algebra: Student Edition...
Algebra
ISBN:9780547587776
Author:HOLT MCDOUGAL
Publisher:HOLT MCDOUGAL
What are the Different Types of Triangles? | Don't Memorise; Author: Don't Memorise;https://www.youtube.com/watch?v=1k0G-Y41jRA;License: Standard YouTube License, CC-BY
Law of Sines AAS, ASA, SSA Ambiguous Case; Author: Mario's Math Tutoring;https://www.youtube.com/watch?v=FPVGb-yWj3s;License: Standard YouTube License, CC-BY
Introduction to Statistics..What are they? And, How Do I Know Which One to Choose?; Author: The Doctoral Journey;https://www.youtube.com/watch?v=HpyRybBEDQ0;License: Standard YouTube License, CC-BY
Triangles | Mathematics Grade 5 | Periwinkle; Author: Periwinkle;https://www.youtube.com/watch?v=zneP1Q7IjgQ;License: Standard YouTube License, CC-BY
What Are Descriptive Statistics And Inferential Statistics?; Author: Amour Learning;https://www.youtube.com/watch?v=MUyUaouisZE;License: Standard Youtube License