
Elementary Geometry for College Students
6th Edition
ISBN: 9781285195698
Author: Daniel C. Alexander, Geralyn M. Koeberlein
Publisher: Cengage Learning
expand_more
expand_more
format_list_bulleted
Textbook Question
Chapter 6.3, Problem 36E
Given:
Find: TM
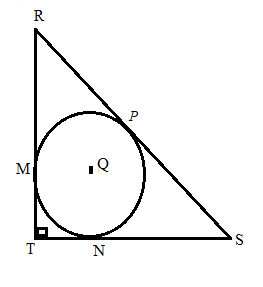
Expert Solution & Answer
Want to see the full answer?
Check out a sample textbook solution
Chapter 6 Solutions
Elementary Geometry for College Students
Ch. 6.1 - For Exercises 1 to 8, use the figure provided....Ch. 6.1 - For Exercises 1 to 8, use the figure provided....Ch. 6.1 - For Exercises 1 to 8, use the figure provided....Ch. 6.1 - For Exercises 1 to 8, use the figure provided....Ch. 6.1 - For Exercises 1 to 8, use the figure provided....Ch. 6.1 - For Exercises 1 to 8, use the figure provided....Ch. 6.1 - For Exercises 1 to 8, use the figure provided....Ch. 6.1 - For Exercises 1 to 8, use the figure provided....Ch. 6.1 - Given: AOOBandOCbisectsACBinO Find: a mAB b mACB c...Ch. 6.1 - Given: ST=12(SR)inQSRisadiameter Find: a mST b mTR...
Ch. 6.1 - Given: QinwhichmAB:mBC:mCA=2:3:4 Find: a mAB b mBC...Ch. 6.1 - Given: mDOE=76and mEOG=82inO EFisadiameter Find: a...Ch. 6.1 - Given: OwithABACand mBOC=72 Find: a mBC b mAB c mA...Ch. 6.1 - In O not shown, OA is a radius, AB is a diameter,...Ch. 6.1 - Given: In O,OCABand OC=6 Find: a AB b BC Exercise...Ch. 6.1 - Prob. 16ECh. 6.1 - Given: Concentric circles with center Q...Ch. 6.1 - AB is the common chord of O and Q. If AB=12 and...Ch. 6.1 - Circles O and Q have the common chord AB. If AB=6,...Ch. 6.1 - Suppose that a circle is divided into three...Ch. 6.1 - Suppose that a circle is divided by points A,B,C,...Ch. 6.1 - Prob. 22ECh. 6.1 - Prob. 23ECh. 6.1 - Prob. 24ECh. 6.1 - Prob. 25ECh. 6.1 - Five points are equally spaced on a circle. A...Ch. 6.1 - A ceiling fan has equally spaced blades. What is...Ch. 6.1 - A wheel has equally spaced lug bolts. What is the...Ch. 6.1 - An amusement park ride the Octopus has eight...Ch. 6.1 - In Exercises 30 and 31, complete each proof....Ch. 6.1 - Prob. 31ECh. 6.1 - In Exercises 32 to 37, write a paragraph proof....Ch. 6.1 - Prob. 33ECh. 6.1 - Prob. 34ECh. 6.1 - Prob. 35ECh. 6.1 - Prob. 36ECh. 6.1 - In Exercises 32 to 37, write a paragraph proof. If...Ch. 6.1 - If MNPQin O, explain why MNPQ is an isosceles...Ch. 6.1 - If STTV, explain why STV is an isosceles triangle.Ch. 6.1 - Prob. 40ECh. 6.1 - In O,OY=5 and XZ=6. If XWWY, find WZ.Ch. 6.2 - Given: mAB=92mDA=114mBC=138 Find:...Ch. 6.2 - Given: mDC=30 and mDABC is trisected at points A...Ch. 6.2 - Given: Circle O with diameter RS, tangent SW,...Ch. 6.2 - Prob. 4ECh. 6.2 - Prob. 5ECh. 6.2 - Is it possible for a a rectangle inscribed in a...Ch. 6.2 - Given: In Q, PR contains Q, MR is a tangent,...Ch. 6.2 - Given: AB and AC are tangent to O, mBC=126 Find:...Ch. 6.2 - Given: Tangent ABand AC to O mACB=68 Find:...Ch. 6.2 - Given: m1=72,mDC=34 Find: a)mABb)m2Ch. 6.2 - Given: m2=36mAB=4mDC Find: a)mABb)m1Ch. 6.2 - Given: m3=42 Find: a)mRTb)mRST Exercises 12,13Ch. 6.2 - Given: RSSTRT Find: a)mRTb)mRSTc)m3 Exercises...Ch. 6.2 - Given: m1=63mRS=3x+6mVT=x Find: mRS Exercises 14,...Ch. 6.2 - Given: m2=124mTV=x+1mSR=3(x+1) Find: mTV Exercises...Ch. 6.2 - Given: m1=71m2=33 Find: mCE and mBD Exercises 16,...Ch. 6.2 - Given: m1=62m2=26 Find: mCE and mBD Exercises 16,...Ch. 6.2 - aHow are R and T related? bFind mR if mT=112....Ch. 6.2 - Prob. 19ECh. 6.2 - A quadrilateral RSTV is circumscribed about a...Ch. 6.2 - In Exercises 21 and 22, complete each proof....Ch. 6.2 - In Exercises 21 and 22, complete each proof....Ch. 6.2 - Prob. 23ECh. 6.2 - Prob. 24ECh. 6.2 - Prob. 25ECh. 6.2 - Prob. 26ECh. 6.2 - An airplane reaches an altitude of 3mi above the...Ch. 6.2 - From the veranda of a beachfront hotel, Manny is...Ch. 6.2 - For the five-pointed star a regular pentagram...Ch. 6.2 - For the six-pointed star a regular hexagram...Ch. 6.2 - A satellite dish in the shape of a regular...Ch. 6.2 - In the figure shown, RSTWVT by the reason AA. Name...Ch. 6.2 - In the figure shown, RXVWXS by the reason AA. Name...Ch. 6.2 - On a fitting for a hex wrench, the distance from...Ch. 6.2 - Given: AB is a diameter of M is the midpoint of...Ch. 6.2 - A surveyor sees a circular planetarium through an...Ch. 6.2 - The larger circle is inscribed in a square with...Ch. 6.2 - In R,QS=2(PT). Also, mP=23. Find mVRS.Ch. 6.2 - Prob. 39ECh. 6.2 - Prob. 40ECh. 6.2 - Prob. 41ECh. 6.2 - In Exercises 39 to 47, provide a paragraph proof....Ch. 6.2 - Prob. 43ECh. 6.2 - Prob. 44ECh. 6.2 - Prob. 45ECh. 6.2 - Prob. 46ECh. 6.2 - Prob. 47ECh. 6.2 - Given concentric circles with center O, ABC is...Ch. 6.2 - Prob. 49ECh. 6.3 - Note: Exercises preceded by an asterisk are of a...Ch. 6.3 - Note: Exercises preceded by an asterisk are of a...Ch. 6.3 - Note: Exercises preceded by an asterisk are of a...Ch. 6.3 - Note: Exercises preceded by an asterisk are of a...Ch. 6.3 - Sketch two circles that have: a No common tangents...Ch. 6.3 - Two congruent intersecting circles B and D not...Ch. 6.3 - Prob. 7ECh. 6.3 - Prob. 8ECh. 6.3 - Prob. 9ECh. 6.3 - Prob. 10ECh. 6.3 - Prob. 11ECh. 6.3 - Prob. 12ECh. 6.3 - Prob. 13ECh. 6.3 - Prob. 14ECh. 6.3 - Prob. 15ECh. 6.3 - Prob. 16ECh. 6.3 - For Exercises 17 to 20. See Theorem 6.3.6. Given:...Ch. 6.3 - For Exercises 17 to 2, See Theorem 6.3.6. Given:...Ch. 6.3 - Prob. 19ECh. 6.3 - For Exercises 17 to 2, See Theorem 6.3.6. Given:...Ch. 6.3 - Prob. 21ECh. 6.3 - In the figure for Exercises 21 to 24,RS is tangent...Ch. 6.3 - In the figure for Exercises 21 to 24,RS is tangent...Ch. 6.3 - Prob. 24ECh. 6.3 - For the two circles in figures a, b, and c, find...Ch. 6.3 - For the two circles in figures a, b, and c, find...Ch. 6.3 - In Exercises 27 to 30, provide a paragraph proof....Ch. 6.3 - Prob. 28ECh. 6.3 - In Exercises 27 to 30, provide a paragraph proof....Ch. 6.3 - Prob. 30ECh. 6.3 - Does it follow from Exercise 30 that ADE is also...Ch. 6.3 - Prob. 32ECh. 6.3 - The cylindrical brush on a vacuum cleaner is...Ch. 6.3 - Prob. 34ECh. 6.3 - Given: Tangents AB,BC,andACtoO at points M, N, and...Ch. 6.3 - Given: Q is inscribed in isosceles right RST. The...Ch. 6.3 - Given: AB is an external tangent to O and Q at...Ch. 6.3 - The center of a circle of radius 3 inches is at a...Ch. 6.3 - The center of a circle of radius 2 inches is at a...Ch. 6.3 - Circles O, P, and Q are tangent as shown at points...Ch. 6.3 - Prob. 41ECh. 6.3 - If the larger gear has 30 teeth and smaller gear...Ch. 6.3 - Prob. 43ECh. 6.3 - In Exercises 44 to 47, prove the stated theorem....Ch. 6.3 - Prob. 45ECh. 6.3 - In Exercises 44 to 47, prove the stated theorem....Ch. 6.3 - Prob. 47ECh. 6.3 - Prob. 48ECh. 6.4 - In Exercises 1 to 8, use the figure provided. If...Ch. 6.4 - Prob. 2ECh. 6.4 - Prob. 3ECh. 6.4 - Prob. 4ECh. 6.4 - Prob. 5ECh. 6.4 - In Exercises 1 to 8, use the figure provided. If...Ch. 6.4 - In Exercises 1 to 8, use the figure provided. If...Ch. 6.4 - Prob. 8ECh. 6.4 - Prob. 9ECh. 6.4 - Prob. 10ECh. 6.4 - X, Y, and Z are on circle O such that mXY=120,...Ch. 6.4 - Construct the two tangent segments to circle P not...Ch. 6.4 - Point V is in the exterior of circle Q not shown...Ch. 6.4 - Prob. 14ECh. 6.4 - Prob. 15ECh. 6.4 - Prob. 16ECh. 6.4 - Prob. 17ECh. 6.4 - a If mRSmTV, write an inequality that compares m1...Ch. 6.4 - a If MNPQ, write an inequality that compares the...Ch. 6.4 - Prob. 20ECh. 6.4 - Quadrilateral ABCD is inscribed in circle P not...Ch. 6.4 - Quadrilateral RSTV is inscribed in circle Q not...Ch. 6.4 - In circle O, points A, B, and C are on the circle...Ch. 6.4 - Prob. 24ECh. 6.4 - Prob. 25ECh. 6.4 - Triangle ABC is inscribed in circle O; AB=5, BC=6,...Ch. 6.4 - Given circle O with mBC=120, and mAC=130. a Which...Ch. 6.4 - Given that mAC:mBC:mAB=4:3:2 in circle O: a Which...Ch. 6.4 - Prob. 29ECh. 6.4 - Circle O has a diameter of length 20cm. Chord AB...Ch. 6.4 - Prob. 31ECh. 6.4 - A tangent ET is constructed to circle Q from...Ch. 6.4 - Prob. 33ECh. 6.4 - Prob. 34ECh. 6.4 - Prob. 35ECh. 6.4 - Prove: In a circle containing two unequal chords,...Ch. 6.4 - In O, chord AB chord CD. Radius OE is...Ch. 6.4 - In P, whose radius has length 8in., mAB=mBC=60....Ch. 6.4 - Prob. 39ECh. 6.CR - The length of the radius of a circle is 15 mm. The...Ch. 6.CR - Find the length of a chord that is 8 cm from the...Ch. 6.CR - Two circles intersect and have a common chord 10...Ch. 6.CR - Two circles intersect and have a common chord 12...Ch. 6.CR - In Review Exercises 5 to 10, BA is tangent to the...Ch. 6.CR - Prob. 6CRCh. 6.CR - In Review Exercises 5 to 10, BA is tangent to the...Ch. 6.CR - In Review Exercises 5 to 10, BA is tangent to the...Ch. 6.CR - Prob. 9CRCh. 6.CR - Prob. 10CRCh. 6.CR - Given:Owithtangentlandm1=46 Find:m2, m3,m4,m5Ch. 6.CR - Given:Owithtangentlandm5=40 Find:m1,m2, m3,m4,Ch. 6.CR - Two circles are concentric. A chord of the larger...Ch. 6.CR - Two parallel chords of a circle each have length...Ch. 6.CR - In Review Exercises 15 to 22, state whether the...Ch. 6.CR - In Review Exercises 15 to 22, state whether the...Ch. 6.CR - In Review Exercises 15 to 22, state whether the...Ch. 6.CR - In Review Exercises 15 to 22, state whether the...Ch. 6.CR - In Review Exercises 15 to 22, state whether the...Ch. 6.CR - Prob. 20CRCh. 6.CR - In Review Exercises 15 to 22, state whether the...Ch. 6.CR - In Review Exercises 15 to 22, state whether the...Ch. 6.CR - Given that CF is a tangent to the circle shown:...Ch. 6.CR - Given that CF is a tangent to the circle shown:...Ch. 6.CR - Given:DF-AC-inO OE=5x+4 OB=2x+19 Find:OECh. 6.CR - Given:OE-OB-inO DF=xx-2 AC=x+28 Find:DEandACCh. 6.CR - In Review Exercises 27 to 29, give a proof for...Ch. 6.CR - In Review Exercises 27 to 29, give a proof for...Ch. 6.CR - In Review Exercises 27 to 29, give a proof for...Ch. 6.CR - Given:OwithdiameterAC-andtangentDE...Ch. 6.CR - A square is inscribed in a circle with a radius of...Ch. 6.CR - A 30-60-90 triangle is inscribed in a circle with...Ch. 6.CR - A circle is inscribed in the right triangle. The...Ch. 6.CR - Given:OisinscribedinABC AB=9,BC=13,AC=10...Ch. 6.CR - In Q with ABQ and CDQ, mABmCD. Also, QPABandQRCD....Ch. 6.CT - a If mAB=88, then mACB=____________. b If mAB=92...Ch. 6.CT - a If mBC=69, then mBOC=_____________. b If mBC=64,...Ch. 6.CT - a If mBAC=24, then mBC=_____________. b If ABAC,...Ch. 6.CT - Complete each theorem: a An angle inscribed in a...Ch. 6.CT - Prob. 5CTCh. 6.CT - Prob. 6CTCh. 6.CT - Prob. 7CTCh. 6.CT - Prob. 8CTCh. 6.CT - In O with diameter AC, OC=5 and AB=6. If M is the...Ch. 6.CT - Prob. 10CTCh. 6.CT - aIf HP=4, PJ=5, and PM=2, find LP. _ bIf HP=x+1,...Ch. 6.CT - Prob. 12CTCh. 6.CT - Construct the tangent line to P at point X.Ch. 6.CT - Prob. 14CTCh. 6.CT - Prob. 15CTCh. 6.CT - Provide the missing statements and reasons in the...
Knowledge Booster
Learn more about
Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, geometry and related others by exploring similar questions and additional content below.Similar questions
- For Exercise 41 to 44, 1 ft3 of liquid corresponds to 7.5 gallons of the liquid. Kiannas aquarium is box-shaped with dimensions of 2 ft by 1 ft by 8 in. What is the water capacity of her aquarium in gallons.arrow_forwardFor Exercise 41 to 44, 1 ft3 of liquid corresponds to 7.5 gallons of the liquid. The gasoline tank on an automobile is box-shaped with dimensions of 24 in. by 20 in. by 9 in. What is the capacity of the automobiles fuel tank in gallons?arrow_forwardGiven : In the figure, a=e=66. Also, YZZW. If YW=14.3 in. and YZ=7.8 in., find the perimeter of XYW to the nearest tenth of an inch.arrow_forward
- Find the length of DF if: a DE=8 and EF=6. b DE=5 and EF=3. Exercises 7-10arrow_forwardFor Exercise 41 to 44, 1 ft3 of liquid corresponds to 7.5 gallons of the liquid. After a devastating rainfall, a basement floor that is 40 ft by 60 ft is covered in 18 in. of water. a How many cubic feet of water must be pumped from the basement? b How many gallons of water are represented by the answer in parta?arrow_forwardIn ABC, M is the midpoint of AB and N is the midpoint of AC. If MN= 3x-11 and BC= 4x24, find the value of x._arrow_forward
- For Exercises 48 and 49, use the formula found in Exercise 47. Find the area of a trapezoid with an altitude of length 513ft and a median of length 214ft.arrow_forwardGiven: RST, with XYRT and YZRS Prove: RXXS=ZTRZarrow_forwardOn a fitting for a hex wrench, the distance from the center o to a vertex is 5mm The length of radius OB of the circle is 10mm. If OCDE at F, how long is FC?arrow_forward
- In ABC, M is the midpoint of AB and N is the midpoint of AC. If MN= 3x-11 and BC= 4x24, find the value of x.arrow_forwardLet AB=a and BC=b. Point M is the midpoint of BC. If AN=23(AB), find the length of NM in terms of a and b.arrow_forwardGeneralize the results found in Exercise 11 and 12 by answering each of the following questions. Assume that the number of sides in each base of the prism is n. For the prism, what is the a number of vertices? b number of lateral edges? c number of base edges? d total of base of edges? e number of lateral faces? f number of bases? g total number of faces?arrow_forward
arrow_back_ios
SEE MORE QUESTIONS
arrow_forward_ios
Recommended textbooks for you
- Algebra & Trigonometry with Analytic GeometryAlgebraISBN:9781133382119Author:SwokowskiPublisher:Cengage
 Elementary Geometry For College Students, 7eGeometryISBN:9781337614085Author:Alexander, Daniel C.; Koeberlein, Geralyn M.Publisher:Cengage,
Elementary Geometry For College Students, 7eGeometryISBN:9781337614085Author:Alexander, Daniel C.; Koeberlein, Geralyn M.Publisher:Cengage, Elementary Geometry for College StudentsGeometryISBN:9781285195698Author:Daniel C. Alexander, Geralyn M. KoeberleinPublisher:Cengage Learning
Elementary Geometry for College StudentsGeometryISBN:9781285195698Author:Daniel C. Alexander, Geralyn M. KoeberleinPublisher:Cengage Learning  Mathematics For Machine TechnologyAdvanced MathISBN:9781337798310Author:Peterson, John.Publisher:Cengage Learning,
Mathematics For Machine TechnologyAdvanced MathISBN:9781337798310Author:Peterson, John.Publisher:Cengage Learning, Holt Mcdougal Larson Pre-algebra: Student Edition...AlgebraISBN:9780547587776Author:HOLT MCDOUGALPublisher:HOLT MCDOUGAL
Holt Mcdougal Larson Pre-algebra: Student Edition...AlgebraISBN:9780547587776Author:HOLT MCDOUGALPublisher:HOLT MCDOUGAL

Algebra & Trigonometry with Analytic Geometry
Algebra
ISBN:9781133382119
Author:Swokowski
Publisher:Cengage

Elementary Geometry For College Students, 7e
Geometry
ISBN:9781337614085
Author:Alexander, Daniel C.; Koeberlein, Geralyn M.
Publisher:Cengage,

Elementary Geometry for College Students
Geometry
ISBN:9781285195698
Author:Daniel C. Alexander, Geralyn M. Koeberlein
Publisher:Cengage Learning

Mathematics For Machine Technology
Advanced Math
ISBN:9781337798310
Author:Peterson, John.
Publisher:Cengage Learning,

Holt Mcdougal Larson Pre-algebra: Student Edition...
Algebra
ISBN:9780547587776
Author:HOLT MCDOUGAL
Publisher:HOLT MCDOUGAL
Quadrilaterals: Missing Angles and Sides; Author: rhornfeck;https://www.youtube.com/watch?v=knVj1O0L2TM;License: Standard YouTube License, CC-BY
STD IX | State Board | Types of Quadrilateral; Author: Robomate;https://www.youtube.com/watch?v=wh0KQ4UB0EU;License: Standard YouTube License, CC-BY