Math
GeometryElementary Geometry for College StudentsGiven that m A C ⌢ : m B C ⌢ : m A B ⌢ = 4 : 3 : 2 in circle O : a) Which arc is largest? b) Which chord is longest?
close solutoin list

Given that m A C ⌢ : m B C ⌢ : m A B ⌢ = 4 : 3 : 2 in circle O : a) Which arc is largest? b) Which chord is longest?

BuyFind

Elementary Geometry for College St...

6th Edition
Daniel C. Alexander + 1 other
Publisher: Cengage Learning
ISBN: 9781285195698
BuyFind

Elementary Geometry for College St...

6th Edition
Daniel C. Alexander + 1 other
Publisher: Cengage Learning
ISBN: 9781285195698

Solutions

Chapter
Section
Problem 1E
Problem 2E
Problem 3E
Problem 4E
Problem 5E
Problem 6E
Problem 7E
Problem 8E
Problem 9E
Problem 10E
Problem 11E
Problem 12E
Problem 13E
Problem 14E
Problem 15E
Problem 16E
Problem 17E
Problem 18E
Problem 19E
Problem 20E
Problem 21E
Problem 22E
Problem 23E
Problem 24E
Problem 25E
Problem 26E
Problem 27E
Problem 28E
Problem 29E
Problem 30E
Problem 31E
Problem 32E
Problem 33E
Problem 34E
Problem 35E
Problem 36E
Problem 37E
Problem 38E
Problem 39E
Chapter 6.4, Problem 28E
Textbook Problem

Given that m A C ⌢ : m B C ⌢ : m A B ⌢ = 4 : 3 : 2 in circle O :

a) Which arc is largest?

b) Which chord is longest?

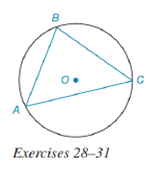
Chapter 6.4, Problem 28E, Given that mAC:mBC:mAB=4:3:2 in circle O: a Which arc is largest? b Which chord is longest?

Expert Solution

Want to see the full answer?

Check out a sample textbook solution.See solution
Chapter 6.4,
Problem 27E
Chapter 6.4,
Problem 29E

Want to see this answer and more?

Experts are waiting 24/7 to provide step-by-step solutions in as fast as 30 minutes!*

See Solution

*Response times vary by subject and question complexity. Median response time is 34 minutes and may be longer for new subjects.

Chapter 6 Solutions

Elementary Geometry for College Students
Show all chapter solutions
Ch. 6.1 - For Exercises 1 to 8, use the figure provided....Ch. 6.1 - For Exercises 1 to 8, use the figure provided....Ch. 6.1 - For Exercises 1 to 8, use the figure provided....Ch. 6.1 - For Exercises 1 to 8, use the figure provided....Ch. 6.1 - For Exercises 1 to 8, use the figure provided....Ch. 6.1 - For Exercises 1 to 8, use the figure provided....Ch. 6.1 - For Exercises 1 to 8, use the figure provided....Ch. 6.1 - For Exercises 1 to 8, use the figure provided....Ch. 6.1 - Given: AOOBandOCbisectsACBinO Find: a mAB b mACB c...Ch. 6.1 - Given: ST=12(SR)inQSRisadiameter Find: a mST b mTR...
Ch. 6.1 - Given: QinwhichmAB:mBC:mCA=2:3:4 Find: a mAB b mBC...Ch. 6.1 - Given: mDOE=76and mEOG=82inO EFisadiameter Find: a...Ch. 6.1 - Given: OwithABACand mBOC=72 Find: a mBC b mAB c mA...Ch. 6.1 - In O not shown, OA is a radius, AB is a diameter,...Ch. 6.1 - Given: In O,OCABand OC=6 Find: a AB b BC Exercise...Ch. 6.1 - Given: Concentric circles with center Q...Ch. 6.1 - Given: Concentric circles with center Q...Ch. 6.1 - AB is the common chord of O and Q. If AB=12 and...Ch. 6.1 - Circles O and Q have the common chord AB. If AB=6,...Ch. 6.1 - Suppose that a circle is divided into three...Ch. 6.1 - Suppose that a circle is divided by points A,B,C,...Ch. 6.1 - Following the pattern of Exercises 20 and 21, what...Ch. 6.1 - Consider a circle or congruent circles, and...Ch. 6.1 - State the measure of the angle formed by the...Ch. 6.1 - State the measure of the angle formed by the...Ch. 6.1 - Five points are equally spaced on a circle. A...Ch. 6.1 - A ceiling fan has equally spaced blades. What is...Ch. 6.1 - A wheel has equally spaced lug bolts. What is the...Ch. 6.1 - An amusement park ride the Octopus has eight...Ch. 6.1 - In Exercises 30 and 31, complete each proof....Ch. 6.1 - In Exercises 30 and 31, complete each proof....Ch. 6.1 - In Exercises 32 to 37, write a paragraph proof....Ch. 6.1 - In Exercises 32 to 37, write a paragraph proof....Ch. 6.1 - In Exercises 32 to 37, write a paragraph proof....Ch. 6.1 - In Exercises 32 to 37, write a paragraph proof. A...Ch. 6.1 - In Exercises 32 to 37, write a paragraph proof. An...Ch. 6.1 - In Exercises 32 to 37, write a paragraph proof. If...Ch. 6.1 - If MNPQin O, explain why MNPQ is an isosceles...Ch. 6.1 - If STTV, explain why STV is an isosceles triangle.Ch. 6.1 - Use a paragraph proof to complete this exercise....Ch. 6.1 - In O,OY=5 and XZ=6. If XWWY, find WZ.Ch. 6.2 - Given: mAB=92mDA=114mBC=138 Find:...Ch. 6.2 - Given: mDC=30 and mDABC is trisected at points A...Ch. 6.2 - Given: Circle O with diameter RS, tangent SW,...Ch. 6.2 - Find mRT if mRST:mRSW=1:5Ch. 6.2 - Find mRST if mRT:mTS=1:4Ch. 6.2 - Is it possible for a a rectangle inscribed in a...Ch. 6.2 - Given: In Q, PR contains Q, MR is a tangent,...Ch. 6.2 - Given: AB and AC are tangent to O, mBC=126 Find:...Ch. 6.2 - Given: Tangent ABand AC to O mACB=68 Find:...Ch. 6.2 - Given: m1=72,mDC=34 Find: a)mABb)m2Ch. 6.2 - Given: m2=36mAB=4mDC Find: a)mABb)m1Ch. 6.2 - Given: m3=42 Find: a)mRTb)mRST Exercises 12,13Ch. 6.2 - Given: RSSTRT Find: a)mRTb)mRSTc)m3 Exercises...Ch. 6.2 - Given: m1=63mRS=3x+6mVT=x Find: mRS Exercises 14,...Ch. 6.2 - Given: m2=124mTV=x+1mSR=3(x+1) Find: mTV Exercises...Ch. 6.2 - Given: m1=71m2=33 Find: mCE and mBD Exercises 16,...Ch. 6.2 - Given: m1=62m2=26 Find: mCE and mBD Exercises 16,...Ch. 6.2 - aHow are R and T related? bFind mR if mT=112....Ch. 6.2 - aHow are S and V related? bFind mV if mS=73....Ch. 6.2 - A quadrilateral RSTV is circumscribed about a...Ch. 6.2 - In Exercises 21 and 22, complete each proof....Ch. 6.2 - In Exercises 21 and 22, complete each proof....Ch. 6.2 - In Exercises 23 to25, complete a paragraph proof....Ch. 6.2 - In Exercises 23 to25, complete a paragraph proof....Ch. 6.2 - In Exercises 23 to25, complete a paragraph proof....Ch. 6.2 - Use the result from Exercise 25 to find m1 if...Ch. 6.2 - An airplane reaches an altitude of 3mi above the...Ch. 6.2 - From the veranda of a beachfront hotel, Manny is...Ch. 6.2 - For the five-pointed star a regular pentagram...Ch. 6.2 - For the six-pointed star a regular hexagram...Ch. 6.2 - A satellite dish in the shape of a regular...Ch. 6.2 - In the figure shown, RSTWVT by the reason AA. Name...Ch. 6.2 - In the figure shown, RXVWXS by the reason AA. Name...Ch. 6.2 - On a fitting for a hex wrench, the distance from...Ch. 6.2 - Given: AB is a diameter of M is the midpoint of...Ch. 6.2 - A surveyor sees a circular planetarium through an...Ch. 6.2 - The larger circle is inscribed in a square with...Ch. 6.2 - In R,QS=2(PT). Also, mP=23. Find mVRS.Ch. 6.2 - In Exercises 39 to 47, provide a paragraph proof....Ch. 6.2 - In Exercises 39 to 47, provide a paragraph proof....Ch. 6.2 - In Exercises 39 to 47, provide a paragraph proof....Ch. 6.2 - In Exercises 39 to 47, provide a paragraph proof....Ch. 6.2 - In Exercises 39 to 47, provide a paragraph proof....Ch. 6.2 - In Exercises 39 to 47, provide a paragraph proof....Ch. 6.2 - In Exercises 39 to 47, provide a paragraph proof....Ch. 6.2 - In Exercises 39 to47, provide a paragraph proof....Ch. 6.2 - Given: Quadrilateral RSTV inscribed in Q Prove:...Ch. 6.2 - Given concentric circles with center O, ABC is...Ch. 6.2 - In the figure, quadrilateral ABCD is inscribed in...Ch. 6.3 - Note: Exercises preceded by an asterisk are of a...Ch. 6.3 - Note: Exercises preceded by an asterisk are of a...Ch. 6.3 - Note: Exercises preceded by an asterisk are of a...Ch. 6.3 - Note: Exercises preceded by an asterisk are of a...Ch. 6.3 - Sketch two circles that have: a No common tangents...Ch. 6.3 - Two congruent intersecting circles B and D not...Ch. 6.3 - In the figure for Exercises 7 to 16, O is the...Ch. 6.3 - In the figure for Exercises 7 to 16, O is the...Ch. 6.3 - In the figure for Exercises 7 to 16, O is the...Ch. 6.3 - In the figure for Exercises 7 to 16, O is the...Ch. 6.3 - In the figure for Exercises 7 to 16, O is the...Ch. 6.3 - In the figure for Exercises 7 to 16, O is the...Ch. 6.3 - In the figure for Exercises 7 to 16, O is the...Ch. 6.3 - In the figure for Exercises 7 to 16, O is the...Ch. 6.3 - In the figure for Exercises 7 to 16, O is the...Ch. 6.3 - In the figure for Exercises 7 to 16, O is the...Ch. 6.3 - For Exercises 17 to 20. See Theorem 6.3.6. Given:...Ch. 6.3 - For Exercises 17 to 2, See Theorem 6.3.6. Given:...Ch. 6.3 - For Exercises 17 to 2, See Theorem 6.3.6. Given:...Ch. 6.3 - For Exercises 17 to 2, See Theorem 6.3.6. Given:...Ch. 6.3 - In the figure for Exercises 21 to 24,RS is tangent...Ch. 6.3 - In the figure for Exercises 21 to 24,RS is tangent...Ch. 6.3 - In the figure for Exercises 21 to 24,RS is tangent...Ch. 6.3 - In the figure for Exercises 21 to 24,RS is tangent...Ch. 6.3 - For the two circles in figures a, b, and c, find...Ch. 6.3 - For the two circles in figures a, b, and c, find...Ch. 6.3 - In Exercises 27 to 30, provide a paragraph proof....Ch. 6.3 - In Exercises 27 to 30, provide a paragraph proof....Ch. 6.3 - In Exercises 27 to 30, provide a paragraph proof....Ch. 6.3 - In Exercises 27 to 30, provide a paragraph proof....Ch. 6.3 - Does it follow from Exercise 30 that ADE is also...Ch. 6.3 - In O not shown, RS is a diameter and T is the...Ch. 6.3 - The cylindrical brush on a vacuum cleaner is...Ch. 6.3 - The drive mechanism on a treadmill is powered by...Ch. 6.3 - Given: Tangents AB,BC,andACtoO at points M, N, and...Ch. 6.3 - Given: Q is inscribed in isosceles right RST. The...Ch. 6.3 - Given: AB is an external tangent to O and Q at...Ch. 6.3 - The center of a circle of radius 3 inches is at a...Ch. 6.3 - The center of a circle of radius 2 inches is at a...Ch. 6.3 - Circles O, P, and Q are tangent as shown at points...Ch. 6.3 - Circles O, P, and Q are tangent as shown for...Ch. 6.3 - If the larger gear has 30 teeth and smaller gear...Ch. 6.3 - For the drawing in Exercise 42, suppose that the...Ch. 6.3 - In Exercises 44 to 47, prove the stated theorem....Ch. 6.3 - In Exercises 44 to 47, prove the stated theorem....Ch. 6.3 - In Exercises 44 to 47, prove the stated theorem....Ch. 6.3 - In Exercises 44 to 47, prove the stated theorem....Ch. 6.3 - The sides of ABC are tangent to D at A and C,...Ch. 6.4 - In Exercises 1 to 8, use the figure provided. If...Ch. 6.4 - In Exercises 1 to 8, use the figure provided. If...Ch. 6.4 - In Exercises 1 to 8, use the figure provided. If...Ch. 6.4 - In Exercises 1 to 8, use the figure provided. If...Ch. 6.4 - In Exercises 1 to 8, use the figure provided. If...Ch. 6.4 - In Exercises 1 to 8, use the figure provided. If...Ch. 6.4 - In Exercises 1 to 8, use the figure provided. If...Ch. 6.4 - In Exercises 1 to 8, use the figure provided. If...Ch. 6.4 - Construct a circle O and choose some point D on...Ch. 6.4 - Construct a circle P and choose three points R, S,...Ch. 6.4 - X, Y, and Z are on circle O such that mXY=120,...Ch. 6.4 - Construct the two tangent segments to circle P not...Ch. 6.4 - Point V is in the exterior of circle Q not shown...Ch. 6.4 - Given circle P and points RPT such that R and T...Ch. 6.4 - Given parallel chords AB, CD, EF, and GH in circle...Ch. 6.4 - Given chords MN, RS, and TV in Q such that QZQYQX,...Ch. 6.4 - Given circle O with radius OT, tangent AD, and the...Ch. 6.4 - a If mRSmTV, write an inequality that compares m1...Ch. 6.4 - a If MNPQ, write an inequality that compares the...Ch. 6.4 - a If mXYmYZ, write an inequality that compares the...Ch. 6.4 - Quadrilateral ABCD is inscribed in circle P not...Ch. 6.4 - Quadrilateral RSTV is inscribed in circle Q not...Ch. 6.4 - In circle O, points A, B, and C are on the circle...Ch. 6.4 - In O, AB=6cm and BC=4cm. a How are mAOB and mBOC...Ch. 6.4 - In O, mAOB=70 and mBOC=30. See the figure above. a...Ch. 6.4 - Triangle ABC is inscribed in circle O; AB=5, BC=6,...Ch. 6.4 - Given circle O with mBC=120, and mAC=130. a Which...Ch. 6.4 - Given that mAC:mBC:mAB=4:3:2 in circle O: a Which...Ch. 6.4 - Given that mA:mB:mC=2:4:3 in circle O: a Which...Ch. 6.4 - Circle O has a diameter of length 20cm. Chord AB...Ch. 6.4 - Circle P has a radius of length 8in. Points A, B,...Ch. 6.4 - A tangent ET is constructed to circle Q from...Ch. 6.4 - Two congruent circles, O and P, do not intersect....Ch. 6.4 - Explain why the following statement is incorrect:...Ch. 6.4 - Prove: In a circle containing two unequal arcs,...Ch. 6.4 - Prove: In a circle containing two unequal chords,...Ch. 6.4 - In O, chord AB chord CD. Radius OE is...Ch. 6.4 - In P, whose radius has length 8in., mAB=mBC=60....Ch. 6.4 - Construct two externally tangent circles where the...Ch. 6.CR - The length of the radius of a circle is 15 mm. The...Ch. 6.CR - Find the length of a chord that is 8 cm from the...Ch. 6.CR - Two circles intersect and have a common chord 10...Ch. 6.CR - Two circles intersect and have a common chord 12...Ch. 6.CR - In Review Exercises 5 to 10, BA is tangent to the...Ch. 6.CR - In Review Exercises 5 to 10, BA is tangent to the...Ch. 6.CR - In Review Exercises 5 to 10, BA is tangent to the...Ch. 6.CR - In Review Exercises 5 to 10, BA is tangent to the...Ch. 6.CR - In Review Exercises 5 to 10, BA is tangent to the...Ch. 6.CR - In Review Exercises 5 to 10, BA is tangent to the...Ch. 6.CR - Given:Owithtangentlandm1=46 Find:m2, m3,m4,m5Ch. 6.CR - Given:Owithtangentlandm5=40 Find:m1,m2, m3,m4,Ch. 6.CR - Two circles are concentric. A chord of the larger...Ch. 6.CR - Two parallel chords of a circle each have length...Ch. 6.CR - In Review Exercises 15 to 22, state whether the...Ch. 6.CR - In Review Exercises 15 to 22, state whether the...Ch. 6.CR - In Review Exercises 15 to 22, state whether the...Ch. 6.CR - In Review Exercises 15 to 22, state whether the...Ch. 6.CR - In Review Exercises 15 to 22, state whether the...Ch. 6.CR - In Review Exercises 15 to 22, state whether the...Ch. 6.CR - In Review Exercises 15 to 22, state whether the...Ch. 6.CR - In Review Exercises 15 to 22, state whether the...Ch. 6.CR - Given that CF is a tangent to the circle shown:...Ch. 6.CR - Given that CF is a tangent to the circle shown:...Ch. 6.CR - Given:DF-AC-inO OE=5x+4 OB=2x+19 Find:OECh. 6.CR - Given:OE-OB-inO DF=xx-2 AC=x+28 Find:DEandACCh. 6.CR - In Review Exercises 27 to 29, give a proof for...Ch. 6.CR - In Review Exercises 27 to 29, give a proof for...Ch. 6.CR - In Review Exercises 27 to 29, give a proof for...Ch. 6.CR - Given:OwithdiameterAC-andtangentDE...Ch. 6.CR - A square is inscribed in a circle with a radius of...Ch. 6.CR - A 30-60-90 triangle is inscribed in a circle with...Ch. 6.CR - A circle is inscribed in the right triangle. The...Ch. 6.CR - Given:OisinscribedinABC AB=9,BC=13,AC=10...Ch. 6.CR - In Q with ABQ and CDQ, mABmCD. Also, QPABandQRCD....Ch. 6.CT - a If mAB=88, then mACB=____________. b If mAB=92...Ch. 6.CT - a If mBC=69, then mBOC=_____________. b If mBC=64,...Ch. 6.CT - a If mBAC=24, then mBC=_____________. b If ABAC,...Ch. 6.CT - Complete each theorem: a An angle inscribed in a...Ch. 6.CT - Given that mAB=106 and mDC=32, find: a m1_ b m2_Ch. 6.CT - Given the tangents with mRT=146, find : a mRST_ b...Ch. 6.CT - Given the tangents with m3=46, find: a mRST_ b...Ch. 6.CT - aBecause point Q is their common center, these...Ch. 6.CT - In O with diameter AC, OC=5 and AB=6. If M is the...Ch. 6.CT - For the circles described and shown, how many...Ch. 6.CT - aIf HP=4, PJ=5, and PM=2, find LP. _ bIf HP=x+1,...Ch. 6.CT - In the figure, TV is a tangent and TVWTXV. Find TV...Ch. 6.CT - Construct the tangent line to P at point X.Ch. 6.CT - aIf mABmCD, write an inequality that compares...Ch. 6.CT - In P not shown, the length of radius PA is 5....Ch. 6.CT - Provide the missing statements and reasons in the...

Additional Math Textbook Solutions

Find more solutions based on key concepts
Show solutions
If f(x)=0g(x)11+t3dt, where g(x)=0cosx[1+sin(t2)]dt, find f(/2).

Single Variable Calculus: Early Transcendentals, Volume I

For each of the following, determine the interval width that would be best for a grouped frequency distribution...

Essentials of Statistics for The Behavioral Sciences (MindTap Course List)

Identify all variables in the research situations listed below and classify them by their level of measurement....

Essentials Of Statistics

Evaluate each expression: 10+42

Elementary Technical Mathematics

Boyles Law states that when a sample of gas is compressed at a constant temperature, the pressure P of the gas ...

Calculus: Early Transcendentals

U.S. Nutritional Supplements Market The size of the U.S. nutritional supplements market from 1999 through 2003 ...

Applied Calculus for the Managerial, Life, and Social Sciences: A Brief Approach

Calculate ss. variance and standMd deviation for the following population of N "" 7 oores: s:. 1 4 3 S 3, ( N.0...

Statistics for The Behavioral Sciences (MindTap Course List)

Polynomial Inequalities Solve the inequality. 3. (x 3)(x + 5)(2x + 5) 0

Precalculus: Mathematics for Calculus (Standalone Book)

In Exercises 516, evaluate the given quantity. log4164

Applied Calculus

For Problems 1-50, solve each equation. Objective 1 3(2a1)2(5a+1)=4(3a+4)

Intermediate Algebra

Newly purchased tires of a particular type are supposed to be filled to a pressure of 30 psi. Let denote the t...

Probability and Statistics for Engineering and the Sciences

Finding Derivatives In Exercises 1-24, find the derivative of the function. See Examples 1, 2, 4, 5, and 8. f(x...

Calculus: An Applied Approach (MindTap Course List)

Find the area of the shaded region. 7.

Multivariable Calculus

Convert each expression in Exercises 25-50 into its technology formula equivalent as in the table in the text. ...

Finite Mathematics and Applied Calculus (MindTap Course List)

3538 Find the volume of the solid by subtracting two volumes. The solid enclosed by the parabolic cylinders y=x...

Calculus (MindTap Course List)

Integration by Substitution In Exercises 43-46, use the specified substitution to find or evaluate the integral...

Calculus: Early Transcendental Functions

In Exercises 1728, use the logarithm identities to obtain the missing quantity.

Finite Mathematics

Criminal Justice: Inmates According to Harper's Index, 50% of all federal inmates are serving time for drug dea...

Understanding Basic Statistics

In Exercises 1 to 6, use the roster method to represent each set. The set of integers that satisfy x2 = 64

Mathematical Excursions (MindTap Course List)

Determine whether the statement is true or false. If it is true, explain why. If it is false, explain why or gi...

Single Variable Calculus

In Problems 9 and 10, at each indicated point, find (a) the slope of the tangent line. (b) the instantaneous ra...

Mathematical Applications for the Management, Life, and Social Sciences

If f is continuous on [0, ], use the substitution u = x to show that 0xf(sinx)dx=20f(sinx)dx

Single Variable Calculus: Early Transcendentals

Evaluate each expression without using a calculator, and write your answers in radians. arctan(33)

Trigonometry (MindTap Course List)

An amount of money that must be deposited today at compound interest to provide a specified lump sum of money i...

Contemporary Mathematics for Business & Consumers

Suppose that G and H are isomorphic groups. Prove that G is abelian if and only if H is abelian.

Elements Of Modern Algebra

Sketching an Ellipse In Exercises 2530, find the center, foci, vertices, and eccentricity of the ellipse, and s...

Calculus of a Single Variable

True or False? In Exercises 113-118, determine whether the statement is true or false. If it is false, explain ...

Calculus: Early Transcendental Functions (MindTap Course List)

In Exercise 12-15, find a logic statement corresponding to the network. Then, find a simpler but equivalent log...

Finite Mathematics for the Managerial, Life, and Social Sciences

True or False: Every series must do one of these: converge absolutely, converge conditionally, or diverge.

Study Guide for Stewart's Single Variable Calculus: Early Transcendentals, 8th

True or False: If F is conservative, then curl F = 0.

Study Guide for Stewart's Multivariable Calculus, 8th

Explain how the process of randomly assigning participants to treatment conditions should prevent a participant...

Research Methods for the Behavioral Sciences (MindTap Course List)

Finding the Average Value of a Function In Exercises 53-58, find the average value of the function over the giv...

Calculus (MindTap Course List)

Explain how holding a participant variable such as gender constant prevents the variable from becoming a confou...

Research Methods for the Behavioral Sciences (MindTap Course List)

The paper referenced in the previous exercise also included data for a second radiologist, Radiologist 2. Based...

Introduction To Statistics And Data Analysis

Cycloid Consider one arch of the cycloid r()=(sin)i+(1cos)j,02 as shown in the figure. Let s() be the arc lengt...

Calculus

Graph each circle. x2+y2-6x+2y+1=0

College Algebra (MindTap Course List)

A sample survey of 54 discount brokers showed that the mean price charged for a trade of 100 shares at 50 per s...

Statistics for Business & Economics, Revised (MindTap Course List)

Finding Parametric EquationsIn Exercises 39 and 40, find a set of parametric equations of the line with the giv...

Multivariable Calculus

What is the purpose of testing whether 1 = 0? If we reject 1 = 0, does it imply a good fit?

STATISTICS F/BUSINESS+ECONOMICS-TEXT

Use a digital micrometer to measure the indicated dimension of each listed object. The length, in inches, of a ...

Mathematics For Machine Technology

Given are five observations for two variables, x and y. a. Develop a scatter diagram for these data. b. What do...

Essentials Of Statistics For Business & Economics

Find the first four terms of each of the recursively defined sequences in 1-8. dk=k(d k1)2 , for every integer ...

Discrete Mathematics With Applications

In Problems 1–10 find the interval and radius of convergence for the given power series. 8.

A First Course in Differential Equations with Modeling Applications (MindTap Course List)

In Exercises 1-8, use your own personal experience with the events described to determine whether a E and F are...

Mathematics: A Practical Odyssey

Reminder Round all answers to two decimal places unless otherwise indicated. Stochastic Population Growth Many ...

Functions and Change: A Modeling Approach to College Algebra (MindTap Course List)

Work Commuting Methods. Public transportation and the automobile are two methods an employee can use to get to ...

Modern Business Statistics with Microsoft Office Excel (with XLSTAT Education Edition Printed Access Card) (MindTap Course List)

For the following exercises, for each pair of functions, find a.(fg)(x) and b.(gf)(x) Simplify the results. Fin...

Calculus Volume 1

Use the following information to answer the next six exercise: On average, a clothing store gets 120 customers ...

Introductory Statistics

Using Latera Recta In Exercises 59-62, sketch the ellipse using the latera recta (see Exercise 58). x29+y216=1.

College Algebra

bartleby
  • Contact Research (Essays)
  • High School Textbooks
  • Literature Guides
  • Essay Help
  • Mobile App
    • © 2021 bartleby. All Rights Reserved.