
Finite Mathematics and Applied Calculus (MindTap Course List)
7th Edition
ISBN: 9781337274203
Author: Stefan Waner, Steven Costenoble
Publisher: Cengage Learning
expand_more
expand_more
format_list_bulleted
Concept explainers
Textbook Question
Chapter 10.2, Problem 17E
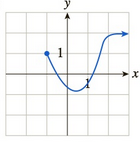
In Exercises 17–24, the graph of a function f is given. Deter- mine whether, at the given point a, f is continuous, discontinuous, or singular. [HINT: See Quick Examples 5 and 6.]
Expert Solution & Answer
Want to see the full answer?
Check out a sample textbook solution
Students have asked these similar questions
In Exercises 27–32, use a graphingutility to graph the function on the closed interval [a, b].Determine whether Rolle’s Theorem can be applied to f on theinterval and, if so, find all values of c in the open interval (a, b)such that f '(c= ' 0.)
f(x)=|x|-1,[-1,1]
Concerned with the number of maintenance visits the rocket can undergo before being out of service, you have been informed that the recent statics show a that after the first journey to the outer space, the rocket was sent to service once, and after that the number of maintenance visits increase by 1 after every journey, for instance, after the second journey, the rocket had to go to service twice before being re-used, three-times after the 3rduse and so on.A. Generate a rule for the number of visits to the maintenance department with respect to space journeys, is this rule arithmetic or geometric.B. How many journeys will it take to for the number of service visits after a certain journey exceed 10?C. The rocket is not to be re-used again if the total number of maintenance visits exceed 50, then how many journeys will a single rocket serve before being out of service?
Concerned with the number of maintenance visits the rocket can undergo before being out of service, you have been informed that the recent statics show a that after the first journey to the outer space, the rocket was sent to service once, and after that the number of maintenance visits increase by 1 after every journey, for instance, after the second journey, the rocket had to go to service twice before being re-used, three-times after the 3rd use and so on.A. Generate a rule for the number of visits to the maintenance department with respect to space journeys, is this rule arithmetic or geometric.B. How many journeys will it take to for the number of service visits after a certain journey exceed 10?C. The rocket is not to be re-used again if the total number of maintenance visits exceed 50, then how many journeys will a single rocket serve before being out of service?While testing the path of the rocket while ascending towards the space, it was found that the rocket rises 480…
Chapter 10 Solutions
Finite Mathematics and Applied Calculus (MindTap Course List)
Ch. 10.1 - In Exercises 14, use the given table of values to...Ch. 10.1 - In Exercises 14, use the given table of values to...Ch. 10.1 - In Exercises 14, use the given table of values to...Ch. 10.1 - In Exercises 14, use the given table of values to...Ch. 10.1 - In Exercises 534, estimate the given limit...Ch. 10.1 - In Exercises 534, estimate the given limit...Ch. 10.1 - In Exercises 534, estimate the given limit...Ch. 10.1 - In Exercises 534, estimate the given limit...Ch. 10.1 - Prob. 9ECh. 10.1 - In Exercises 534, estimate the given limit...
Ch. 10.1 - Prob. 11ECh. 10.1 - In Exercises 534, estimate the given limit...Ch. 10.1 - In Exercises 534, estimate the given limit...Ch. 10.1 - Prob. 14ECh. 10.1 - In Exercises 534, estimate the given limit...Ch. 10.1 - In Exercises 534, estimate the given limit...Ch. 10.1 - Prob. 17ECh. 10.1 - Prob. 18ECh. 10.1 - Prob. 19ECh. 10.1 - Prob. 20ECh. 10.1 - In Exercises 534, estimate the given limit...Ch. 10.1 - In Exercises 534, estimate the given limit...Ch. 10.1 - In Exercises 534, estimate the given limit...Ch. 10.1 - Prob. 24ECh. 10.1 - In Exercises 534, estimate the given limit...Ch. 10.1 - In Exercises 534, estimate the given limit...Ch. 10.1 - In Exercises 534, estimate the given limit...Ch. 10.1 - In Exercises 534, estimate the given limit...Ch. 10.1 - Prob. 29ECh. 10.1 - In Exercises 534, estimate the given limit...Ch. 10.1 - In Exercises 534, estimate the given limit...Ch. 10.1 - Prob. 32ECh. 10.1 - Prob. 33ECh. 10.1 - Prob. 34ECh. 10.1 - Prob. 35ECh. 10.1 - Prob. 36ECh. 10.1 - Prob. 37ECh. 10.1 - Prob. 38ECh. 10.1 - In Exercises 3548 the graph of f is given. Use the...Ch. 10.1 - In Exercises 3548 the graph of f is given. Use the...Ch. 10.1 - In Exercises 3548 the graph of f is given. Use the...Ch. 10.1 - Prob. 42ECh. 10.1 - Prob. 43ECh. 10.1 - Prob. 44ECh. 10.1 - In Exercises 3548 the graph of f is given. Use the...Ch. 10.1 - In Exercises 3548 the graph of f is given. Use the...Ch. 10.1 - In Exercises 3548 the graph of f is given. Use the...Ch. 10.1 - In Exercises 3548 the graph of f is given. Use the...Ch. 10.1 - Doctorates in Mexico The annual number of PhD...Ch. 10.1 - Housing Starts The number s(t) ofhousing starts...Ch. 10.1 - Funding for NASA up to 1966 The percentage of the...Ch. 10.1 - Funding for NASA up to 1966 (Compare Exercise 51.)...Ch. 10.1 - Scientific Research: 19832003 The number of...Ch. 10.1 - Scientific Research: 19832003 The percentage of...Ch. 10.1 - SAT Scores by Income The following bar graph shows...Ch. 10.1 - SAT Scores by Income The following bar graph shows...Ch. 10.1 - Flash Crash The graph shows a rough representation...Ch. 10.1 - Flash Crash The graph shows a rough representation...Ch. 10.1 - Home Prices The following graph shows the values...Ch. 10.1 - Home Prices: Optimist Projection The following...Ch. 10.1 - Prob. 61ECh. 10.1 - Prob. 62ECh. 10.1 - Prob. 63ECh. 10.1 - Prob. 64ECh. 10.1 - Prob. 65ECh. 10.1 - Prob. 66ECh. 10.1 - Prob. 67ECh. 10.1 - Prob. 68ECh. 10.1 - What is wrong with the following statement?...Ch. 10.1 - Prob. 70ECh. 10.1 - Prob. 71ECh. 10.1 - Prob. 72ECh. 10.1 - Prob. 73ECh. 10.1 - Prob. 74ECh. 10.2 - In Exercises 114 the graph of a function f is...Ch. 10.2 - In Exercises 114 the graph of a function f is...Ch. 10.2 - In Exercises 114 the graph of a function f is...Ch. 10.2 - Prob. 4ECh. 10.2 - In Exercises 114 the graph of a function f is...Ch. 10.2 - In Exercises 114 the graph of a function f is...Ch. 10.2 - In Exercises 114 the graph of a function f is...Ch. 10.2 - Prob. 8ECh. 10.2 - Prob. 9ECh. 10.2 - Prob. 10ECh. 10.2 - Prob. 11ECh. 10.2 - Prob. 12ECh. 10.2 - Prob. 13ECh. 10.2 - Prob. 14ECh. 10.2 - In Exercises 15 and 16, identify which (if any) of...Ch. 10.2 - In Exercises 15 and 16, identify which (if any) of...Ch. 10.2 - In Exercises 1724, the graph of a function f is...Ch. 10.2 - In Exercises 1724, the graph of a function f is...Ch. 10.2 - Prob. 19ECh. 10.2 - In Exercises 1724, the graph of a function f is...Ch. 10.2 - In Exercises 1724, the graph of a function f is...Ch. 10.2 - In Exercises 1724, the graph of a function f is...Ch. 10.2 - Prob. 23ECh. 10.2 - In Exercises 1724, the graph of a function f is...Ch. 10.2 - In Exercises 2532, use a graph of f or some other...Ch. 10.2 - In Exercises 2532, use a graph of f or some other...Ch. 10.2 - In Exercises 2532, use a graph of f or some other...Ch. 10.2 - In Exercises 2532, use a graph of f or some other...Ch. 10.2 - In Exercises 2532, use a graph of f or some other...Ch. 10.2 - Prob. 30ECh. 10.2 - In Exercises 2532, use a graph of f or some other...Ch. 10.2 - Prob. 32ECh. 10.2 - In Exercises 3342, use a graph to determine...Ch. 10.2 - In Exercises 3342, use a graph to determine...Ch. 10.2 - Prob. 35ECh. 10.2 - Prob. 36ECh. 10.2 - In Exercises 3342, use a graph to determine...Ch. 10.2 - Prob. 38ECh. 10.2 - In Exercises 3342, use a graph to determine...Ch. 10.2 - Prob. 40ECh. 10.2 - Prob. 41ECh. 10.2 - Prob. 42ECh. 10.2 - Multiple choice: If f is defined on all real...Ch. 10.2 - Prob. 44ECh. 10.2 - Prob. 45ECh. 10.2 - Multiple: choice If f is defined everywhere except...Ch. 10.2 - Prob. 47ECh. 10.2 - Prob. 48ECh. 10.2 - True or false? The graph of a function that is...Ch. 10.2 - Prob. 50ECh. 10.2 - Prob. 51ECh. 10.2 - Prob. 52ECh. 10.2 - Prob. 53ECh. 10.2 - Prob. 54ECh. 10.2 - Prob. 55ECh. 10.2 - Prob. 56ECh. 10.3 - In Exercises 14, complete the given sentence. The...Ch. 10.3 - In Exercises 14, complete the given sentence. The...Ch. 10.3 - Prob. 3ECh. 10.3 - Prob. 4ECh. 10.3 - In Exercises 520, determine whether the given...Ch. 10.3 - In Exercises 520, determine whether the given...Ch. 10.3 - In Exercises 520, determine whether the given...Ch. 10.3 - In Exercises 520, determine whether the given...Ch. 10.3 - In Exercises 520, determine whether the given...Ch. 10.3 - Prob. 10ECh. 10.3 - Prob. 11ECh. 10.3 - Prob. 12ECh. 10.3 - Prob. 13ECh. 10.3 - Prob. 14ECh. 10.3 - Prob. 15ECh. 10.3 - Prob. 16ECh. 10.3 - Prob. 17ECh. 10.3 - Prob. 18ECh. 10.3 - Prob. 19ECh. 10.3 - Prob. 20ECh. 10.3 - Prob. 21ECh. 10.3 - Prob. 22ECh. 10.3 - Prob. 23ECh. 10.3 - In Exercises 21-74, calculate the limit...Ch. 10.3 - In Exercises 21-74, calculate the limit...Ch. 10.3 - Prob. 26ECh. 10.3 - In Exercises 21-74, calculate the limit...Ch. 10.3 - Prob. 28ECh. 10.3 - Prob. 29ECh. 10.3 - Prob. 30ECh. 10.3 - In Exercises 21-74, calculate the limit...Ch. 10.3 - Prob. 32ECh. 10.3 - In Exercises 21-74, calculate the limit...Ch. 10.3 - Prob. 34ECh. 10.3 - Prob. 35ECh. 10.3 - Prob. 36ECh. 10.3 - In Exercises 21-74, calculate the limit...Ch. 10.3 - Prob. 38ECh. 10.3 - Prob. 39ECh. 10.3 - Prob. 40ECh. 10.3 - Prob. 41ECh. 10.3 - Prob. 42ECh. 10.3 - Prob. 43ECh. 10.3 - Prob. 44ECh. 10.3 - Prob. 45ECh. 10.3 - Prob. 46ECh. 10.3 - Prob. 47ECh. 10.3 - Prob. 48ECh. 10.3 - Prob. 49ECh. 10.3 - Prob. 50ECh. 10.3 - Prob. 51ECh. 10.3 - Prob. 52ECh. 10.3 - Prob. 53ECh. 10.3 - Prob. 54ECh. 10.3 - Prob. 55ECh. 10.3 - Prob. 56ECh. 10.3 - In Exercises 21-74, calculate the limit...Ch. 10.3 - Prob. 58ECh. 10.3 - Prob. 59ECh. 10.3 - Prob. 60ECh. 10.3 - In Exercises 21-74, calculate the limit...Ch. 10.3 - Prob. 62ECh. 10.3 - In Exercises 21-74, calculate the limit...Ch. 10.3 - In Exercises 21-74, calculate the limit...Ch. 10.3 - In Exercises 21-74, calculate the limit...Ch. 10.3 - In Exercises 21-74, calculate the limit...Ch. 10.3 - In Exercises 21-74, calculate the limit...Ch. 10.3 - Prob. 68ECh. 10.3 - In Exercises 21-74, calculate the limit...Ch. 10.3 - Prob. 70ECh. 10.3 - In Exercises 21-74, calculate the limit...Ch. 10.3 - Prob. 72ECh. 10.3 - Prob. 73ECh. 10.3 - Prob. 74ECh. 10.3 - In Exercises 75-88, identify all singular points...Ch. 10.3 - Prob. 76ECh. 10.3 - Prob. 77ECh. 10.3 - Prob. 78ECh. 10.3 - Prob. 79ECh. 10.3 - Prob. 80ECh. 10.3 - In Exercises 75-88, identify all singular points...Ch. 10.3 - Prob. 82ECh. 10.3 - In Exercises 75-88, identify all singular points...Ch. 10.3 - Prob. 84ECh. 10.3 - Prob. 85ECh. 10.3 - Prob. 86ECh. 10.3 - Prob. 87ECh. 10.3 - Prob. 88ECh. 10.3 - Prob. 89ECh. 10.3 - Prob. 90ECh. 10.3 - Prob. 91ECh. 10.3 - Movie Advertising The percentage of movie...Ch. 10.3 - Law Enforcement in the 1980s and 1990s The cost of...Ch. 10.3 - Prob. 94ECh. 10.3 - Prob. 95ECh. 10.3 - SAT Scores by Income The following bar graph shows...Ch. 10.3 - Prob. 97ECh. 10.3 - Prob. 98ECh. 10.3 - Prob. 99ECh. 10.3 - Prob. 100ECh. 10.3 - Prob. 101ECh. 10.3 - Prob. 102ECh. 10.3 - Prob. 103ECh. 10.3 - Prob. 104ECh. 10.3 - Why was the following marked wrong? What is the...Ch. 10.3 - Why was the following marked wrong? What is the...Ch. 10.3 - Your friend Karin tells you that f(x)=1/(x2)2...Ch. 10.3 - Prob. 108ECh. 10.3 - Prob. 109ECh. 10.3 - Prob. 110ECh. 10.3 - Prob. 111ECh. 10.3 - Prob. 112ECh. 10.3 - What is wrong with the following statement? If...Ch. 10.3 - What is wrong with the following statement? If...Ch. 10.3 - Prob. 115ECh. 10.3 - Prob. 116ECh. 10.3 - Prob. 117ECh. 10.3 - Prob. 118ECh. 10.4 - In Exercises 118, calculate the average rate of...Ch. 10.4 - In Exercises 118, calculate the average rate of...Ch. 10.4 - In Exercises 118, calculate the average rate of...Ch. 10.4 - In Exercises 118, calculate the average rate of...Ch. 10.4 - In Exercises 118, calculate the average rate of...Ch. 10.4 - In Exercises 118, calculate the average rate of...Ch. 10.4 - In Exercises 118, calculate the average rate of...Ch. 10.4 - In Exercises 118, calculate the average rate of...Ch. 10.4 - In Exercises 118, calculate the average rate of...Ch. 10.4 - In Exercises 118, calculate the average rate of...Ch. 10.4 - In Exercises 118, calculate the average rate of...Ch. 10.4 - In Exercises 118, calculate the average rate of...Ch. 10.4 - In Exercises 118, calculate the average rate of...Ch. 10.4 - In Exercises 118, calculate the average rate of...Ch. 10.4 - In Exercises 118, calculate the average rate of...Ch. 10.4 - In Exercises 118, calculate the average rate of...Ch. 10.4 - In Exercises 118, calculate the average rate of...Ch. 10.4 - In Exercises 118, calculate the average rate of...Ch. 10.4 - In Exercises 1924, calculate the average rate of...Ch. 10.4 - In Exercises 1924, calculate the average rate of...Ch. 10.4 - In Exercises 1924, calculate the average rate of...Ch. 10.4 - Prob. 22ECh. 10.4 - Prob. 23ECh. 10.4 - Prob. 24ECh. 10.4 - World Military Expenditure The following table...Ch. 10.4 - Education Expenditure The following table shows...Ch. 10.4 - Crude Oil Production: Mexico The following table...Ch. 10.4 - Offshore Crude Oil Production: Mexico The...Ch. 10.4 - Subprime Mortgages during the Housing Crisis The...Ch. 10.4 - Subprime Mortgage Debt during the Housing Crisis...Ch. 10.4 - Immigration to Ireland The following graph shows...Ch. 10.4 - Emigration from Ireland The following graph shows...Ch. 10.4 - Science Research in the United States The...Ch. 10.4 - Prob. 34ECh. 10.4 - Prob. 35ECh. 10.4 - College Basketball: Women The following chart...Ch. 10.4 - Funding for the Arts State governments in the...Ch. 10.4 - Funding for the Arts The U.S. federal government...Ch. 10.4 - Market Index Joe Downs runs a small investment...Ch. 10.4 - Prob. 42ECh. 10.4 - Crude Oil Prices The price per barrel of crude oil...Ch. 10.4 - Median Home Prices The median home price in the...Ch. 10.4 - Prob. 45ECh. 10.4 - Prob. 46ECh. 10.4 - The 2003 SARS Outbreak In the early stages of the...Ch. 10.4 - Prob. 48ECh. 10.4 - The 2014 Ebola Outbreak In the first 6 months of...Ch. 10.4 - Prob. 50ECh. 10.4 - Prob. 51ECh. 10.4 - Prob. 52ECh. 10.4 - Prob. 53ECh. 10.4 - Prob. 54ECh. 10.4 - Describe three ways we have used to determine the...Ch. 10.4 - Prob. 56ECh. 10.4 - Prob. 57ECh. 10.4 - Prob. 58ECh. 10.4 - Sketch the graph of a function whose average rate...Ch. 10.4 - Prob. 60ECh. 10.4 - Prob. 61ECh. 10.4 - Prob. 62ECh. 10.4 - Prob. 63ECh. 10.4 - Prob. 64ECh. 10.4 - Prob. 65ECh. 10.4 - Prob. 66ECh. 10.4 - Prob. 67ECh. 10.4 - Prob. 68ECh. 10.5 - In Exercises 14, estimate the derivative from the...Ch. 10.5 - In Exercises 14, estimate the derivative from the...Ch. 10.5 - In Exercises 14, estimate the derivative from the...Ch. 10.5 - Prob. 4ECh. 10.5 - Consider the functions in Exercises 58 as...Ch. 10.5 - Consider the functions in Exercises 58 as...Ch. 10.5 - Prob. 7ECh. 10.5 - Prob. 8ECh. 10.5 - In Exercises 912 the function gives the cost to...Ch. 10.5 - In Exercises 912 the function gives the cost to...Ch. 10.5 - Prob. 11ECh. 10.5 - Prob. 12ECh. 10.5 - In Exercises 1316 the graph of a function is shown...Ch. 10.5 - In Exercises 1316 the graph of a function is shown...Ch. 10.5 - In Exercises 1316 the graph of a function is shown...Ch. 10.5 - Prob. 16ECh. 10.5 - In Exercises 1722, say at which labeled point the...Ch. 10.5 - Prob. 18ECh. 10.5 - Prob. 19ECh. 10.5 - In Exercises 1722, say at which labeled point the...Ch. 10.5 - Prob. 21ECh. 10.5 - Prob. 22ECh. 10.5 - In each of Exercises 2326, three slopes are given....Ch. 10.5 - In each of Exercises 2326, three slopes are given....Ch. 10.5 - Prob. 25ECh. 10.5 - Prob. 26ECh. 10.5 - In Exercises 2730, find the approximate...Ch. 10.5 - Prob. 28ECh. 10.5 - Prob. 29ECh. 10.5 - Prob. 30ECh. 10.5 - Prob. 31ECh. 10.5 - Prob. 32ECh. 10.5 - Prob. 33ECh. 10.5 - Which is correct? The derivative function f(x)...Ch. 10.5 - Let f have the graph shown. a. The average rate of...Ch. 10.5 - Prob. 36ECh. 10.5 - Prob. 37ECh. 10.5 - In Exercises 3740, use a quick approximation to...Ch. 10.5 - In Exercises 3740, use a quick approximation to...Ch. 10.5 - Prob. 40ECh. 10.5 - In Exercises 41-48, estimate the indicated...Ch. 10.5 - Prob. 42ECh. 10.5 - In Exercises 41-48, estimate the indicated...Ch. 10.5 - In Exercises 41-48, estimate the indicated...Ch. 10.5 - Prob. 45ECh. 10.5 - Prob. 46ECh. 10.5 - In Exercises 41-48, estimate the indicated...Ch. 10.5 - Prob. 48ECh. 10.5 - In Exercises 4954, (a) use any method to estimate...Ch. 10.5 - Prob. 50ECh. 10.5 - Prob. 51ECh. 10.5 - Prob. 52ECh. 10.5 - In Exercises 4954, (a) use any method to estimate...Ch. 10.5 - Prob. 54ECh. 10.5 - In Exercises 55-58, estimate the given quantity....Ch. 10.5 - Prob. 56ECh. 10.5 - Prob. 57ECh. 10.5 - Prob. 58ECh. 10.5 - In Exercises 5964, match the graph of f to the...Ch. 10.5 - In Exercises 5964, match the graph of f to the...Ch. 10.5 - In Exercises 5964, match the graph of f to the...Ch. 10.5 - In Exercises 5964, match the graph of f to the...Ch. 10.5 - In Exercises 5964, match the graph of f to the...Ch. 10.5 - In Exercises 5964, match the graph of f to the...Ch. 10.5 - In Exercises 6568 the graph of a function is...Ch. 10.5 - Prob. 66ECh. 10.5 - Prob. 67ECh. 10.5 - Prob. 68ECh. 10.5 - Prob. 69ECh. 10.5 - Prob. 70ECh. 10.5 - In Exercises 6972 the graph of the derivative of a...Ch. 10.5 - Prob. 72ECh. 10.5 - Prob. 73ECh. 10.5 - Prob. 74ECh. 10.5 - Prob. 75ECh. 10.5 - Prob. 76ECh. 10.5 - Temperatures on Mars The air temperature one...Ch. 10.5 - Prob. 78ECh. 10.5 - Demand Suppose the demand for a new brand of...Ch. 10.5 - Demand Suppose the demand for an old brand of TV...Ch. 10.5 - Oil Imports from Mexico The following graph shows...Ch. 10.5 - Oil Production in Mexico The following graph shows...Ch. 10.5 - Prob. 83ECh. 10.5 - Prob. 84ECh. 10.5 - Prob. 85ECh. 10.5 - Prob. 86ECh. 10.5 - Crude Oil Prices The price per barrel of crude oil...Ch. 10.5 - Median Home Prices The median home price in the...Ch. 10.5 - The 2003 SARS Outbreak In the early stages of the...Ch. 10.5 - Prob. 90ECh. 10.5 - Prob. 91ECh. 10.5 - Prob. 92ECh. 10.5 - Prob. 93ECh. 10.5 - Prob. 94ECh. 10.5 - Prob. 95ECh. 10.5 - Prob. 96ECh. 10.5 - Prob. 97ECh. 10.5 - Prob. 98ECh. 10.5 - Prob. 99ECh. 10.5 - Prob. 100ECh. 10.5 - Prob. 101ECh. 10.5 - Prob. 102ECh. 10.5 - Prob. 103ECh. 10.5 - Prob. 104ECh. 10.5 - Prob. 105ECh. 10.5 - Prob. 106ECh. 10.5 - Prob. 107ECh. 10.5 - Prob. 108ECh. 10.5 - Prob. 109ECh. 10.5 - Prob. 110ECh. 10.5 - Prob. 111ECh. 10.5 - Company Cs profits are given by P(0)=1 millionand...Ch. 10.5 - Prob. 113ECh. 10.5 - During the 1-month period starting last January 1,...Ch. 10.5 - If the derivative of f is zero at a point, what do...Ch. 10.5 - Prob. 116ECh. 10.5 - Prob. 117ECh. 10.5 - Prob. 118ECh. 10.5 - Prob. 119ECh. 10.5 - Prob. 120ECh. 10.5 - Prob. 121ECh. 10.5 - Prob. 122ECh. 10.5 - Prob. 123ECh. 10.5 - Prob. 124ECh. 10.5 - Prob. 125ECh. 10.5 - Prob. 126ECh. 10.5 - Prob. 127ECh. 10.5 - Prob. 128ECh. 10.5 - Prob. 129ECh. 10.5 - Prob. 130ECh. 10.6 - In Exercises 1-14, compute f(a) algebraically for...Ch. 10.6 - Prob. 2ECh. 10.6 - In Exercises 1-14, compute f(a) algebraically for...Ch. 10.6 - In Exercises 1-14, compute f(a) algebraically for...Ch. 10.6 - In Exercises 1-14, compute f(a) algebraically for...Ch. 10.6 - Prob. 6ECh. 10.6 - Prob. 7ECh. 10.6 - Prob. 8ECh. 10.6 - Prob. 9ECh. 10.6 - Prob. 10ECh. 10.6 - In Exercises 1-14, compute f(a) algebraically for...Ch. 10.6 - In Exercises 1-14, compute f(a) algebraically for...Ch. 10.6 - In Exercises 1-14, compute f(a) algebraically for...Ch. 10.6 - In Exercises 1-14, compute f(a) algebraically for...Ch. 10.6 - In Exercises 15-28, compute the derivative...Ch. 10.6 - In Exercises 15-28, compute the derivative...Ch. 10.6 - Prob. 17ECh. 10.6 - Prob. 18ECh. 10.6 - Prob. 19ECh. 10.6 - Prob. 20ECh. 10.6 - In Exercises 15-28, compute the derivative...Ch. 10.6 - Prob. 22ECh. 10.6 - Prob. 23ECh. 10.6 - Prob. 24ECh. 10.6 - In Exercises 15-28, compute the derivative...Ch. 10.6 - In Exercises 15-28, compute the derivative...Ch. 10.6 - In Exercises 15-28, compute the derivative...Ch. 10.6 - Prob. 28ECh. 10.6 - Prob. 29ECh. 10.6 - Prob. 30ECh. 10.6 - Prob. 31ECh. 10.6 - Prob. 32ECh. 10.6 - In Exercises 29-38, compute the indicated...Ch. 10.6 - Prob. 34ECh. 10.6 - Prob. 35ECh. 10.6 - Prob. 36ECh. 10.6 - In Exercises 29-38, compute the indicated...Ch. 10.6 - Prob. 38ECh. 10.6 - In Exercises39-44, find the equation of the...Ch. 10.6 - Prob. 40ECh. 10.6 - Prob. 41ECh. 10.6 - Prob. 42ECh. 10.6 - In Exercises39-44, find the equation of the...Ch. 10.6 - Prob. 44ECh. 10.6 - Velocity If a stone is dropped from a height of...Ch. 10.6 - Prob. 46ECh. 10.6 - Oil Imports from Mexico Daily crude oil imports to...Ch. 10.6 - Prob. 48ECh. 10.6 - Bottled Water Sales The following chart shows the...Ch. 10.6 - Bottled Water Sales The following chart shows...Ch. 10.6 - Ecology Increasing numbers of manatees have been...Ch. 10.6 - SAT Scores by Income The following graph shown...Ch. 10.6 - Television Advertising The cost, in thousands of...Ch. 10.6 - Prob. 54ECh. 10.6 - Of the three methods (numerical, graphical, and...Ch. 10.6 - Explain why we cannot put h=0 in the formula...Ch. 10.6 - You just got your derivatives test back, and you...Ch. 10.6 - Your friend just got his derivatives test back and...Ch. 10.6 - Prob. 59ECh. 10.6 - Your third friend just got her derivatives test...Ch. 10.6 - Prob. 61ECh. 10.6 - Prob. 62ECh. 10.6 - Prob. 63ECh. 10.6 - One cannot put h=0 in the formula...Ch. 10 - In Exercise 1-4, numerically estimate whether the...Ch. 10 - In Exercise 1-4, numerically estimate whether the...Ch. 10 - In Exercise 1-4, numerically estimate whether the...Ch. 10 - In Exercise 1-4, numerically estimate whether the...Ch. 10 - In Exercises 5 and 6 the graph of a function f is...Ch. 10 - In Exercises 5 and 6 the graph of a function f is...Ch. 10 - In Exercises 730, calculate the limit...Ch. 10 - In Exercises 730, calculate the limit...Ch. 10 - In Exercises 730, calculate the limit...Ch. 10 - In Exercises 730, calculate the limit...Ch. 10 - In Exercises 730, calculate the limit...Ch. 10 - In Exercises 730, calculate the limit...Ch. 10 - In Exercises 730, calculate the limit...Ch. 10 - In Exercises 730, calculate the limit...Ch. 10 - In Exercises 730, calculate the limit...Ch. 10 - In Exercises 730, calculate the limit...Ch. 10 - In Exercises 730, calculate the limit...Ch. 10 - In Exercises 730, calculate the limit...Ch. 10 - In Exercises 730, calculate the limit...Ch. 10 - In Exercises 730, calculate the limit...Ch. 10 - In Exercises 730, calculate the limit...Ch. 10 - In Exercises 730, calculate the limit...Ch. 10 - Prob. 23RECh. 10 - Prob. 24RECh. 10 - Prob. 25RECh. 10 - Prob. 26RECh. 10 - In Exercises 730, calculate the limit...Ch. 10 - Prob. 28RECh. 10 - Prob. 29RECh. 10 - Prob. 30RECh. 10 - Prob. 31RECh. 10 - Prob. 32RECh. 10 - Prob. 33RECh. 10 - Prob. 34RECh. 10 - Prob. 35RECh. 10 - Prob. 36RECh. 10 - Prob. 37RECh. 10 - Prob. 38RECh. 10 - Prob. 39RECh. 10 - Prob. 40RECh. 10 - In Exercises 4144, use the definition of the...Ch. 10 - Prob. 42RECh. 10 - Prob. 43RECh. 10 - Prob. 44RECh. 10 - Prob. 45RECh. 10 - Prob. 46RECh. 10 - Prob. 47RECh. 10 - Prob. 48RECh. 10 - Prob. 49RECh. 10 - Prob. 50RECh. 10 - Real Estate Marjory Duffin has persuaded John...Ch. 10 - Prob. 52RECh. 10 - Prob. 53RECh. 10 - Rising Sea Level Marjory Duffin recently purchased...Ch. 10 - Prob. 55RECh. 10 - Prob. 56RECh. 10 - Prob. 57RECh. 10 - Prob. 58RECh. 10 - Prob. 1CSCh. 10 - Prob. 2CSCh. 10 - What is the marginal emission charge (derivative...Ch. 10 - We said that the revised policy provided an...Ch. 10 - What change in C(q) wouldmake 8 million tons the...Ch. 10 - If the scenario in Exercise 5 took place, what...Ch. 10 - Because of intense lobbying by the utility...Ch. 10 - Suppose that instead of imposing a fixed charge...
Knowledge Booster
Learn more about
Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, calculus and related others by exploring similar questions and additional content below.Similar questions
- Find the Wronskian for the set of functions.{1, x, x2, x3}arrow_forwardTheorem 1 in Section 2.4 states the following: "If f and g are continuous functions, then f + g is continuous." Does it follow logically that if f and g are not continuous, then f + g is not continuous?arrow_forward8 Examine holomorphism for given function f(z) = |z|arrow_forward
- Exercise 4.1.6. For each of the following formulas, find the largest subset X ⊆ R such that g: X → R is a function. (4) g(x) = {sqrt(x) if x∈X and x ≥ 0, x+1, if x ∈ X and x ≤ 0}.arrow_forwardHint: for each closed subset C of Y, f**-1(C) is closed in X. g(f**-1(V)) ? Book: Principles of Tobologyarrow_forward
arrow_back_ios
arrow_forward_ios
Recommended textbooks for you
- Algebra & Trigonometry with Analytic GeometryAlgebraISBN:9781133382119Author:SwokowskiPublisher:Cengage


Algebra & Trigonometry with Analytic Geometry
Algebra
ISBN:9781133382119
Author:Swokowski
Publisher:Cengage

Limits and Continuity; Author: The Organic Chemistry Tutor;https://www.youtube.com/watch?v=9brk313DjV8;License: Standard YouTube License, CC-BY