
College Physics
11th Edition
ISBN: 9781305952300
Author: Raymond A. Serway, Chris Vuille
Publisher: Cengage Learning
expand_more
expand_more
format_list_bulleted
Concept explainers
Textbook Question
Chapter 13, Problem 74AP
Figure P13.74 shows a crude model of an insect wing. The mass m represents the entire mass of the wing, which pivots about the fulcrum F. The spring represents the surrounding connective tissue. Motion of the wing corresponds to vibration of the spring. Suppose the mass of the wing is 0.30 g and the effective spring constant of the tissue is 4.7 ×10−4 N/m. If the mass m moves up and down a distance of 2.0 mm from its position of equilibrium, what is the maximum speed of the outer tip of the wing?
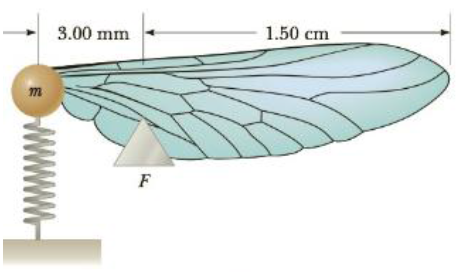
Figure P13.74
Expert Solution & Answer
Trending nowThis is a popular solution!

Chapter 13 Solutions
College Physics
Ch. 13.1 - A block on the end of a horizontal spring is...Ch. 13.1 - For a simple harmonic oscillator, which of the...Ch. 13.2 - When an object moving in simple harmonic motion is...Ch. 13.3 - An object of mass m is attached to a horizontal...Ch. 13.3 - Prob. 13.5QQCh. 13.4 - If the amplitude of a system moving in simple...Ch. 13.5 - A simple pendulum is suspended from the ceiling of...Ch. 13.5 - A pendulum dork depends on the period of a...Ch. 13.5 - The period of a simple pendulum is measured to be...Ch. 13 - An objectspring system undergoes simple harmonic...
Ch. 13 - If an objectspring system is hung vertically and...Ch. 13 - The spring in Figure CQ13.3 is stretched from its...Ch. 13 - If the spring constant shown in Figure CQ13.3 is...Ch. 13 - If the spring shown in Figure CQ13.3 is com...Ch. 13 - If a spring is cut in half, what happens to its...Ch. 13 - A pendulum bob is made from a sphere filled with...Ch. 13 - A block connected to a horizontal spring is in...Ch. 13 - (a) Is a bouncing ball an example of simple...Ch. 13 - If a grandfather clock were running slow, how...Ch. 13 - What happens to the speed of a wave on a string...Ch. 13 - Prob. 12CQCh. 13 - Waves are traveling on a uniform string under...Ch. 13 - Identify each of the following waves as either...Ch. 13 - A block, of mass m = 0.60 kg attached to a spring...Ch. 13 - A spring oriented vertically is attached to a hard...Ch. 13 - The force constant of a spring is 137 N/m. Find...Ch. 13 - A spring is hung from a ceiling, and an object...Ch. 13 - A biologist hangs a sample of mass 0.725 kg on a...Ch. 13 - An archer must exert a force of 375 N on the...Ch. 13 - A spring 1.50 m long with force constant 475 N/m...Ch. 13 - A block of mass m = 2.00 kg is attached to a...Ch. 13 - A slingshot consists of a light leather cup...Ch. 13 - An archer pulls her bowstring back 0.400 m by...Ch. 13 - A student pushes the 1.50-kg block in Figure...Ch. 13 - An automobile having a mass of 1.00 103 kg is...Ch. 13 - A 10.0-g bullet is fired into, and embeds itself...Ch. 13 - An object-spring system moving with simple...Ch. 13 - A horizontal block-spring system with the block on...Ch. 13 - A 0.250-kg block attached to a light spring...Ch. 13 - A block-spring system consists of a spring with...Ch. 13 - A 0.40-kg object connected to a light spring with...Ch. 13 - At an outdoor market, a bunch of bananas attached...Ch. 13 - A student stretches a spring, attaches a 1.00-kg...Ch. 13 - A horizontal spring attached to a wall has a force...Ch. 13 - An object moves uniformly around a circular path...Ch. 13 - The wheel in the simplified engine of Figure...Ch. 13 - The period of motion of an object-spring system is...Ch. 13 - A vertical spring stretches 3.9 cm when a 10.-g...Ch. 13 - When four people with a combined mass of 320 kg...Ch. 13 - The position of an object connected to a spring...Ch. 13 - A harmonic oscillator is described by the function...Ch. 13 - A 326-g object is attached to a spring and...Ch. 13 - An object executes simple harmonic motion with an...Ch. 13 - A 2.00-kg object on a frictionless horizontal...Ch. 13 - A spring of negligible mass stretches 3.00 cm from...Ch. 13 - Given that x = A cos (t) is a sinusoidal function...Ch. 13 - A man enters a tall tower, needing to know its...Ch. 13 - A simple pendulum has a length of 52.0 cm and...Ch. 13 - A seconds pendulum is one that moves through its...Ch. 13 - A clock is constructed so that it keeps perfect...Ch. 13 - A coat hanger of mass m = 0.238 kg oscillates on a...Ch. 13 - The free-fall acceleration on Mars is 3.7 m/s2....Ch. 13 - A simple pendulum is 5.00 in long. (a) What is the...Ch. 13 - The sinusoidal wave shown in Figure P13.41 is...Ch. 13 - An object attached to a spring vibrates with...Ch. 13 - Prob. 43PCh. 13 - The distance between two successive minima of a...Ch. 13 - A harmonic wave is traveling along a rope. It is...Ch. 13 - A bat can detect small objects, such as an insect,...Ch. 13 - Orchestra instruments are commonly tuned to match...Ch. 13 - Prob. 48PCh. 13 - Prob. 49PCh. 13 - Workers attach a 25.0-kg mass to one end of a...Ch. 13 - A piano siring of mass per unit length 5.00 103...Ch. 13 - A student taking a quiz finds on a reference sheet...Ch. 13 - Prob. 53PCh. 13 - An astronaut on the Moon wishes to measure the...Ch. 13 - A simple pendulum consists of a ball of mass 5.00...Ch. 13 - A string is 50.0 cm long and has a mass of 3.00 g....Ch. 13 - Tension is maintained in a string as in Figure...Ch. 13 - The elastic limit of a piece of steel wire is 2.70...Ch. 13 - A 2.65-kg power line running between two towers...Ch. 13 - Prob. 60PCh. 13 - Prob. 61PCh. 13 - The position of a 0.30-kg object attached to a...Ch. 13 - An object of mass 2.00 kg is oscillating freely on...Ch. 13 - Prob. 64APCh. 13 - A simple pendulum has mass 1.20 kg and length...Ch. 13 - A 0.500-kg block is released from rest and slides...Ch. 13 - A 3.00-kg object is fastened to a light spring,...Ch. 13 - A 5.00-g bullet moving with an initial speed of...Ch. 13 - A large block P executes horizontal simple...Ch. 13 - A spring in a toy gun has a spring constant of...Ch. 13 - A light balloon filled with helium of density...Ch. 13 - An object of mass m is connected to two rubber...Ch. 13 - Assume a hole is drilled through the center of the...Ch. 13 - Figure P13.74 shows a crude model of an insect...Ch. 13 - A 2.00-kg block hangs without vibrating at the end...Ch. 13 - A system consists of a vertical spring with force...
Knowledge Booster
Learn more about
Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, physics and related others by exploring similar questions and additional content below.Similar questions
- A pendulum of length L and mass M has a spring of force constant k connected to it at a distance h below its point of suspension (Fig. P12.65). Find the frequency of vibration of the system for small values of the amplitude (small ). Assume the vertical suspension rod of length L is rigid, but ignore its mass. Figure P12.65arrow_forwardA block of mass M is connected to a spring of mass m and oscillates in simple harmonic motion on a frictionless, horizontal track (Fig. P12.69). The force constant of the spring is k, and the equilibrium length is . Assume all portions of the spring oscillate in phase and the velocity of a segment of the spring of length dx is proportional to the distance x from the fixed end; that is, vx = (x/) v. Also, notice that the mass of a segment of the spring is dm = (m/) dx. Find (a) the kinetic energy of the system when the block has a speed v and (b) the period of oscillation. Figure P12.69arrow_forwardA small ball of mass M is attached to the end of a uniform rod of equal mass M and length L that is pivoted at the top (Fig. P12.59). Determine the tensions in the rod (a) at the pivot and (b) at the point P when the system is stationary. (c) Calculate the period of oscillation for small displacements from equilibrium and (d) determine this period for L = 2.00 m. Figure P12.59arrow_forward
- A watch balance wheel (Fig. P15.25) has a period of oscillation of 0.250 s. The wheel is constructed so that its mass of 20.0 g is concentrated around a rim of radius 0.500 cm. What are (a) the wheels moment of inertia and (b) the torsion constant of the attached spring? Figure P15.23arrow_forwardAn object of mass m1 = 9.00 kg is in equilibrium when connected to a light spring of constant k = 100 N/m that is fastened to a wall as shown in Figure P12.67a. A second object, m2 = 7.00 kg, is slowly pushed up against m1, compressing the spring by the amount A = 0.200 m (see Fig. P12.67b). The system is then released, and both objects start moving to the right on the frictionless surface. (a) When m1 reaches the equilibrium point, m2 loses contact with m1 (see Fig. P12.67c) and moves to the right with speed v. Determine the value of v. (b) How far apart are the objects when the spring is fully stretched for the first time (the distance D in Fig. P12.67d)? Figure P12.67arrow_forwardReview. A system consists of a spring with force constant k = 1 250 N/m, length L = 1.50 m, and an object of mass m = 5.00 kg attached to the end (Fig. P15.49). The object is placed at the level of the point of attachment with the spring unstretched, at position yi = L, and then it is released so that it swings like a pendulum. (a) Find the y position of the object at the lowest point. (b) Will the pendulums period be greater or less than the period of a simple pendulum with the same mass m and length L? Explain. Figure PI 5.49arrow_forward
- A spherical bob of mass m and radius R is suspended from a fixed point by a rigid rod of negligible mass whose length from the point of support to the center of the bob is L (Fig. P16.75). Find the period of small oscillation. N The frequency of a physical pendulum comprising a nonuniform rod of mass 1.25 kg pivoted at one end is observed to be 0.667 Hz. The center of mass of the rod is 40.0 cm below the pivot point. What is the rotational inertia of the pendulum around its pivot point?arrow_forwardA very light rigid rod of length 0.500 m extends straight out from one end of a meter-stick. The combination is suspended from a pivot at the upper end of the rod as shown in Figure P12.31. The combination is then pulled out by a small angle and released. (a) Determine the period of oscillation of the system. (b) By what percentage does the period differ from the period of a simple pendulum 1.00 m long? Figure P12.31arrow_forwardA lightweight spring with spring constant k = 225 N/m is attached to a block of mass m1 = 4.50 kg on a frictionless, horizontal table. The blockspring system is initially in the equilibrium configuration. A second block of mass m2 = 3.00 kg is then pushed against the first block, compressing the spring by x = 15.0 cm as in Figure P16.77A. When the force on the second block is removed, the spring pushes both blocks to the right. The block m2 loses contact with the springblock 1 system when the blocks reach the equilibrium configuration of the spring (Fig. P16.77B). a. What is the subsequent speed of block 2? b. Compare the speed of block 1 when it again passes through the equilibrium position with the speed of block 2 found in part (a). 77. (a) The energy of the system initially is entirely potential energy. E0=U0=12kymax2=12(225N/m)(0.150m)2=2.53J At the equilibrium position, the total energy is the total kinetic energy of both blocks: 12(m1+m2)v2=12(4.50kg+3.00kg)v2=(3.75kg)v2=2.53J Therefore, the speed of each block is v=2.53J3.75kg=0.822m/s (b) Once the second block loses contact, the first block is moving at the speed found in part (a) at the equilibrium position. The energy 01 this spring-block 1 system is conserved, so when it returns to the equilibrium position, it will be traveling at the same speed in the opposite direction, or v=0.822m/s. FIGURE P16.77arrow_forward
- Which of the following statements is not true regarding a massspring system that moves with simple harmonic motion in the absence of friction? (a) The total energy of the system remains constant. (b) The energy of the system is continually transformed between kinetic and potential energy. (c) The total energy of the system is proportional to the square of the amplitude. (d) The potential energy stored in the system is greatest when the mass passes through the equilibrium position. (e) The velocity of the oscillating mass has its maximum value when the mass passes through the equilibrium position.arrow_forwardA block of mass m rests on a frictionless, horizontal surface and is attached to two springs with spring constants k1 and k2 (Fig. P16.22). It is displaced to the right and released. Find an expression for the angular frequency of oscillation of the resulting simple harmonic motion. FIGURE P16.22 Problems 22 and 81.arrow_forward
arrow_back_ios
arrow_forward_ios
Recommended textbooks for you
 Principles of Physics: A Calculus-Based TextPhysicsISBN:9781133104261Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning
Principles of Physics: A Calculus-Based TextPhysicsISBN:9781133104261Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning Physics for Scientists and Engineers: Foundations...PhysicsISBN:9781133939146Author:Katz, Debora M.Publisher:Cengage Learning
Physics for Scientists and Engineers: Foundations...PhysicsISBN:9781133939146Author:Katz, Debora M.Publisher:Cengage Learning Physics for Scientists and Engineers with Modern ...PhysicsISBN:9781337553292Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning
Physics for Scientists and Engineers with Modern ...PhysicsISBN:9781337553292Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning Physics for Scientists and EngineersPhysicsISBN:9781337553278Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning
Physics for Scientists and EngineersPhysicsISBN:9781337553278Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning

Principles of Physics: A Calculus-Based Text
Physics
ISBN:9781133104261
Author:Raymond A. Serway, John W. Jewett
Publisher:Cengage Learning

Physics for Scientists and Engineers: Foundations...
Physics
ISBN:9781133939146
Author:Katz, Debora M.
Publisher:Cengage Learning

Physics for Scientists and Engineers with Modern ...
Physics
ISBN:9781337553292
Author:Raymond A. Serway, John W. Jewett
Publisher:Cengage Learning

Physics for Scientists and Engineers
Physics
ISBN:9781337553278
Author:Raymond A. Serway, John W. Jewett
Publisher:Cengage Learning
SIMPLE HARMONIC MOTION (Physics Animation); Author: EarthPen;https://www.youtube.com/watch?v=XjkUcJkGd3Y;License: Standard YouTube License, CC-BY