
Concept explainers
The temperature distribution in a tapered conical cooling fin (Fig. P28.48) is described by the following differential equation, which has been nondimensionalized
where
where
Solve this equation for the temperature distribution using finite difference methods. Use second-order accurate finite difference analogues for the derivatives. Write a computer program to obtain the solution and plot temperature versus axial distance for various values of
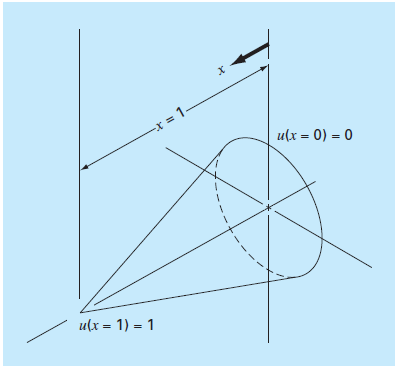
FIGURE P28.48
Want to see the full answer?
Check out a sample textbook solution
Chapter 28 Solutions
EBK NUMERICAL METHODS FOR ENGINEERS
- We performed the experiment to measure the thermal conductivity of 2 materials (Brass & Steel) in the laboratory and measured the following tabulated values: Material 1 - BRASS (Diameter = 25mm) Power Temperature (°C) Q' (W) 2 3 4 6 7 8 1 5 9 14.6 78.9 77.5 76 50.2 46.7 42.4 36.1 34.6 33.6 Material 2 - STEEL (Diameter = 25mm) Power Temperature (°C) 7 Q' (W) 14.25 2 3 1 9 88.6 87.4 85 34.1 33.4 32.7 CALCULATE THE FOLLOWING: MATERIAL 1 - BRASS Calculation for Brass Quantities Calculated Values Power (Q') W Area of cross section (A) m2 Difference in Temperature between two points (AT) °C Difference in distance between two points (Ax) m Thermal conductivity of brass (k,) W/m'C MATERIAL 2 - STEEL Calculation for Steel Quantities Calculated Values Power (Q') W Area of cross section (A) m? Difference in Temperature between two points (AT) "C Difference in distance between two points (Ax) m Thermal conductivity of steel (k,) W/m°Carrow_forward(SI units) Aluminum has a density of 2.70g/cm³ at room temperature (20°C). Determine its density at 650°C, using data in Table 4.1 for reference.arrow_forwardQ.No.5: (a) Develop an equation by using pi-theorem for the shear stress in a fluid flowing in a pipe assuming that the stress is a function of the diameter and the roughness of the pipe, and the density, viscosity and velocity of the fluid. (b) A model of a torpedo is tested in a towing tank at a velocity of 24.4 m/s. The prototype is expected to attain a velocity of 246 m/min in 15.6°C water. (i) What model scale has been used? (ii) What would be the model speed it tested in a wind tunnel under a pressure of 290 psi and at constant temperature 26.77°C?arrow_forward
- The following table lists temperatures and specific volumes of water vapor at two pressures: p = 1.5 MPa v(m³/kg) p = 1.0 MPa T ("C) v(m³/kg) T ("C) 200 0.2060 200 0.1325 240 280 0.2275 0.2480 240 280 0.1483 0.1627 Data encountered in solving problems often do not fall exactly on the grid of values provided by property tables, and linear interpolation between adjacent table entries becomes necessary. Using the data provided here, estimate i. the specific volume at T= 240 °Č, p = 1.25 MPa, in m/kg ii. the temperature at p = 1.5 MPa, v = 0.1555 m/kg, in °C ii. the specific volume at T = 220 °C, p = 1.4 MPa, in m'/kgarrow_forward100 80 60 40 20 0.002 0.004 0.006 0.008 0.01 0.012 Strain, in/in. FIGURE P1.17 1.18 Use Problem 1.17 to graphically determine the following: a. Modulus of resilience b. Toughness Hint: The toughness (u) can be determined by calculating the area under the stress-strain curve u = de where & is the strain at fracture. The preceding integral can be approxi- mated numerically by using a trapezoidal integration technique: u, = Eu, = o, + o e, - 6) %3D c. If the specimen is loaded to 40 ksi only and the lateral strain was found to be -0.00057 in./in., what is Poisson's ratio of this metal? d. If the specimen is loaded to 70 ksi only and then unloaded, what is the permanent strain? Stress, ksiarrow_forwardA two dimensional square plate (with 2m on each side) is subjected to the boundary conditions shown below. y T= 300 °C T= 70 °C 3 m T= 70°C 3 m T= 70 °C 1) Plot the temperature distribution obtained by the numerical solution a. using a uniform grid size of 0.5 m (Ax=Ay=0.5) b. using a uniform grid size of 0.1 m (Ax=Ay=0.1) 2) Plot temperatures (obtained by exact and two numerical solutions) as a function of a. x at y=1.0 m b. x at y=1.5 m c. y at x-1.0 m d. y at x-1.5 marrow_forward
- QI: Write a material balances and pressure drop equations for the following pipes network: 90 is 55 600 m 45 254 mm 10 600 m 254 mm C 35 +ve 600 m C 152 mm 600 152 mm 15 60V 600 m 152 mm 600 m 152 mmarrow_forwardQUESTION-) 236 °C steam flows in a pipe which features are given below. Inner and outer diameters of pipe are 300 mm and 320 mm. Coefficient of heat transmission is 40 W/mK. It's external ambient is air and it's temperature is 20 °C. Take the temperature of the pipe's external surface 180 °C. It is known that the internal temp convection coefficient is 600 W/m^2K and external heat transfer coefficient is 5,9109 W/m^2K The pipe's length is 500 meter. You need to add the radiation in the calculation. The rate of the radiation emissivity is 0.85. You can take the environmental surface temp directly. Please calculate the heat loss of pipe.arrow_forwardQUESTION-) 236 °C steam flows in a pipe which features are given below. Inner and outer diameters of pipe are 300 mm and 320 mm. Coefficient of heat transmission is 40 W/mK. It's external ambient is air and it's temperature is 20 °C. Take the temperature of the pipe's external surface 180 °C. It is known that the internal temp convection coefficient is 600 W/m^2K and external heat transfer coefficient is 5,9109 W/m^2K The pipe's length is 500 meter. You need to add the radiation in the calculation. The rate of the radiation emissivity is 0.85. You can take the environmental surface temp directly. a-) Please draw this question on the resistance network. b-) Please calculate the heat loss of pipe. c-) By applying insulation to this pipe, it is desired to reduce the heat loss to 20% of the uninsulated loss (option a). Calculate the insulation thickness accordingly. Take glass wool as insulation material.(Conductivity of glass wool = 0.040 W/mK.) Given, The temperature of steam inside the…arrow_forward
- Give True or False for the following: 1.In liquids and gases, heat transmission is caused by conduction and convection 2.The surface geometry is the important factor in convection heat transfer 3. The heat transfer by conduction from heated surface to the adjacent layer of fluid, 4. The heat transfer is increased in the fin when &> 1 5.The unit of the thermal diffusivity is m²/s 6. Temperature change between the materials interfaces is attributed to the thermal contact resistance 7. A material that has a low heat capacity will have a large thermal diffusivity. 8. Heat conduction flowing from one side to other depends directly on thickness 9.Fin efficiency is the ratio of the fin heat dissipation with that of no fin 10.The critical radius is represented the ratio of the convicted heat transfer to the thermal conductivityarrow_forwardyo 9:1V i %A LO äbä 20 A ladder 13 ft long is leaning against a wall. The bottom of the ladder is being pulled away from the wall at the constant rate of 6 ft/min. How fast is the top of the ladder moving down the wall when the bottom of the * ?ladder is5 ft from the wall 13 y 6 ft/min 2.5 3.5arrow_forwardThe Philippine ten-peso coin (P10) is the second largest denomination coin of the Philippine peso. The current version, issued since 2018, has a diameter of d, = 27.0000 mm and a thickness of họ = 2.0500 mm. When the coin is subjected to a temperature change of 100 C°, the diameter of the coin increases by 0.11 percent. Suppose the coefficient of linear expansion of the coin is unknown, which of the following expressions should you use to compute for it? *arrow_forward
 Principles of Heat Transfer (Activate Learning wi...Mechanical EngineeringISBN:9781305387102Author:Kreith, Frank; Manglik, Raj M.Publisher:Cengage Learning
Principles of Heat Transfer (Activate Learning wi...Mechanical EngineeringISBN:9781305387102Author:Kreith, Frank; Manglik, Raj M.Publisher:Cengage Learning
