Chapter 33, Problem 50PE

Integrated Concepts

In supernovas, neutrinos are produced in huge amounts. They were detected from the 1987A supernova in the Magellanic Cloud, which is about 120,000 light years away from the Earth (relatively close to our Milky Way galaxy). If neutrinos have a mass, they cannot travel at the 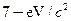speed of light, but it their mass is small, they can get close. (a) Suppose a neutrino with a mass has a kinetic energy of 700 keV. Find the relativistic quantity 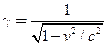for it (b) If the neutrino leaves the 1987A supernova at the same time as a photon and both travel to Earth, how much sooner does the photon arrive? This is not a large time difference, given that it is impossible to know which neutrino left with which photon and the peer ef?ciency of the neutrino detectors. Thus, the fact that neutrinos were observed within hours of the brightening of the supernova only places an upper limit on the neutrino’s mass. (Hint: You may need to use a series expansion to find if for the neutrino, since its (is so large.)