
Elementary Geometry For College Students, 7e
7th Edition
ISBN: 9781337614085
Author: Alexander, Daniel C.; Koeberlein, Geralyn M.
Publisher: Cengage,
expand_more
expand_more
format_list_bulleted
Textbook Question
Chapter 8.2, Problem 41E
For Exercises 41 and 42, the sides of square ABCD are trisected at the indicated points.
Find the ratio:
| a)
|
b)
|
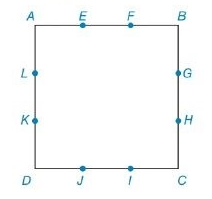
Exercises 41 and 42
Expert Solution & Answer
Want to see the full answer?
Check out a sample textbook solution
Chapter 8 Solutions
Elementary Geometry For College Students, 7e
Ch. 8.1 - Suppose that two triangles have equal areas. Are...Ch. 8.1 - The area of the square is 12, and the area of the...Ch. 8.1 - Consider the information in Exercise 2, but...Ch. 8.1 - If MNPQ is a rhombus, which formula from this...Ch. 8.1 - In rhombus MNPQ, how does the length of the...Ch. 8.1 - When the diagonals of rhombus MNPQ are drawn, how...Ch. 8.1 - Prob. 7ECh. 8.1 - Are ABC and DEF congruent? Exercises 7, 8Ch. 8.1 - Prob. 9ECh. 8.1 - In Exercises 9 to 18, find the areas of the...
Ch. 8.1 - In Exercises 9 to 18, find the areas of the...Ch. 8.1 - Prob. 12ECh. 8.1 - In Exercises 9 to 18, find the areas of the...Ch. 8.1 - In Exercises 9 to 18, find the areas of the...Ch. 8.1 - In Exercises 9 to 18, find the areas of the...Ch. 8.1 - In Exercises 9 to 18, find the areas of the...Ch. 8.1 - In Exercises 9 to 18, find the areas of the...Ch. 8.1 - Prob. 18ECh. 8.1 - In Exercises 19 to 22, find the area of the shaded...Ch. 8.1 - Prob. 20ECh. 8.1 - In Exercises 19 to 22, find the area of the shaded...Ch. 8.1 - In Exercises 19 to 22, find the area of the shaded...Ch. 8.1 - A triangular corner of a store has been roped off...Ch. 8.1 - Carpeting is to be purchased for the family room...Ch. 8.1 - The exterior wall the gabled end of the house...Ch. 8.1 - The roof of the house shown needs to be...Ch. 8.1 - A beach tent is designed so that one side is open....Ch. 8.1 - Gary and Carolyn plan to build the deck shown. a...Ch. 8.1 - A square yard is a square with sides 1 yard in...Ch. 8.1 - The following problem is based on this theorem: A...Ch. 8.1 - For Exercise 31 and 32, X is the midpoint of VT...Ch. 8.1 - Prob. 32ECh. 8.1 - Prob. 33ECh. 8.1 - In Exercises 34 to 36, provide paragraph proofs....Ch. 8.1 - In Exercises 34 to 36, provide paragraph proofs....Ch. 8.1 - In Exercises 34 to 36, provide paragraph proofs....Ch. 8.1 - Given: The area of right ABC not shown is 40in2....Ch. 8.1 - The lengths of the legs of a right triangle are...Ch. 8.1 - Given: ABC, whose sides are 13 in., 14 in., and 15...Ch. 8.1 - Prob. 40ECh. 8.1 - If the length of the base of a rectangle is...Ch. 8.1 - If the length of the base of a rectangle is...Ch. 8.1 - Prob. 43ECh. 8.1 - Prob. 44ECh. 8.1 - The algebra method of FOIL multiplication is...Ch. 8.1 - Use the square configuration to complete the...Ch. 8.1 - In Exercises 47 to 50, use the fact that the area...Ch. 8.1 - Prob. 48ECh. 8.1 - Prob. 49ECh. 8.1 - In Exercises 47 to 50, use the fact that the area...Ch. 8.1 - The area of a rectangle is 48in2. Where x is the...Ch. 8.1 - The perimeter of the rectangle is 32 cm. Where x...Ch. 8.1 - Square DEFG is inscribed in right ABC, as shown....Ch. 8.1 - TV bisects STR of STR. ST=6 and TR=9. If the area...Ch. 8.1 - Prob. 55ECh. 8.1 - Prob. 56ECh. 8.2 - In Exercises 1 to 8, find the perimeter of each...Ch. 8.2 - In Exercises 1 to 8, find the perimeter of each...Ch. 8.2 - In Exercises 1 to 8, find the perimeter of each...Ch. 8.2 - In Exercises 1 to 8, find the perimeter of each...Ch. 8.2 - In Exercises 1 to 8, find the perimeter of each...Ch. 8.2 - In Exercises 1 to 8, find the perimeter of each...Ch. 8.2 - In Exercises 1 to 8, find the perimeter of each...Ch. 8.2 - In Exercises 1 to 8, find the perimeter of each...Ch. 8.2 - In Exercises 9 and 10, use Herons Formula. Find...Ch. 8.2 - Prob. 10ECh. 8.2 - For Exercises 11 and 12, use Brahmaguptas Formula....Ch. 8.2 - For Exercises 11 and 12, use Brahmaguptas Formula....Ch. 8.2 - In Exercises 13 to 18, find the area of the given...Ch. 8.2 - In Exercises 13 to 18, find the area of the given...Ch. 8.2 - In Exercises 13 to 18, find the area of the given...Ch. 8.2 - Prob. 16ECh. 8.2 - Prob. 17ECh. 8.2 - In Exercises 13 to 18, find the area of the given...Ch. 8.2 - In a triangle of perimeter 76 in., the length of...Ch. 8.2 - In a triangle whose area is 72 in2, the base has a...Ch. 8.2 - A trapezoid has an area of 96 cm2. If the altitude...Ch. 8.2 - The numerical difference between the area of a...Ch. 8.2 - Prob. 23ECh. 8.2 - Find the ratio A1A2 of the areas of two similar...Ch. 8.2 - In Exercises 25 and 26, give a paragraph form of...Ch. 8.2 - In Exercises 25 and 26, give a paragraph form of...Ch. 8.2 - In Exercises 27 to 30, find the area of the figure...Ch. 8.2 - In Exercises 27 to 30, find the area of the figure...Ch. 8.2 - In Exercises 27 to 30, find the area of the figure...Ch. 8.2 - In Exercises 27 to 30, find the area of the figure...Ch. 8.2 - Mary Frances has a rectangular garden plot that...Ch. 8.2 - Prob. 32ECh. 8.2 - Farmer Watson wishes to fence a rectangular plot...Ch. 8.2 - The farmer in Exercise 33 has decided to take the...Ch. 8.2 - Prob. 35ECh. 8.2 - Find the perimeter of the room in Exercise 35.Ch. 8.2 - Examine several rectangles, each with a perimeter...Ch. 8.2 - Examine several rectangles, each with an area of...Ch. 8.2 - Square RSTV is inscribed in square WXYZ, as shown....Ch. 8.2 - Square RSTV is inscribed in square WXYZ, as shown....Ch. 8.2 - For Exercises 41 and 42, the sides of square ABCD...Ch. 8.2 - For Exercises 41 and 42, the sides of square ABCD...Ch. 8.2 - Prob. 43ECh. 8.2 - Prob. 44ECh. 8.2 - For Exercises 45 and 46, use this information: Let...Ch. 8.2 - Prob. 46ECh. 8.2 - Prob. 47ECh. 8.2 - Prob. 48ECh. 8.2 - For Exercises 48 and 49, use the formula found in...Ch. 8.2 - Prove that the area of a square whose diagonal has...Ch. 8.2 - Prob. 51ECh. 8.2 - Prob. 52ECh. 8.2 - The shaded region is that of a trapezoid....Ch. 8.2 - Trapezoid ABCD not shown is inscribed in O so that...Ch. 8.2 - Each side of square RSTV has length 8. Point W...Ch. 8.2 - For the cyclic quadrilateral MNPQ, the sides have...Ch. 8.2 - Prob. 57ECh. 8.3 - Find the area of a square with a sides of length...Ch. 8.3 - Find the area of a square with a a perimeter of...Ch. 8.3 - Find the area of an equilateral triangle with a...Ch. 8.3 - Find the area of an equiangular triangle with a a...Ch. 8.3 - In a regular polygon, each central angle measures...Ch. 8.3 - In a regular polygon, each interior angle measures...Ch. 8.3 - For a regular hexagon, the length of the apothem...Ch. 8.3 - For a regular hexagon, the length of the radius is...Ch. 8.3 - In a particular type of regular polygon, the...Ch. 8.3 - In a particular type of regular polygon, the...Ch. 8.3 - Prob. 11ECh. 8.3 - If the area (A=12aP) and the perimeter of a...Ch. 8.3 - Find the area of a square with apothem a = 3.2 cm...Ch. 8.3 - Find the area of an equilateral triangle with...Ch. 8.3 - Find the area of an equilateral triangle with...Ch. 8.3 - Find the area of a square with apothem a = 8.2 ft...Ch. 8.3 - In Exercises 17 to 30, use the formula A=12aP to...Ch. 8.3 - In Exercises 17 to 30, use the formula A=12aP to...Ch. 8.3 - In Exercises 17 to 30, use the formula A=12aP to...Ch. 8.3 - In Exercises 17 to 30, use the formula A=12aP to...Ch. 8.3 - Prob. 21ECh. 8.3 - In Exercises 17 to 30, use the formula A=12aP to...Ch. 8.3 - In Exercises 17 to 30, use the formula A=12aP to...Ch. 8.3 - In Exercises 17 to 30, use the formula A=12aP to...Ch. 8.3 - In Exercises 17 to 30, use the formula A=12aP to...Ch. 8.3 - In Exercises 17 to 30, use the formula A=12aP to...Ch. 8.3 - In Exercises 17 to 30, use the formula A=12aP to...Ch. 8.3 - In Exercises 17 to 30, use the formula A=12aP to...Ch. 8.3 - In Exercises 17 to 30, use the formula A=12aP to...Ch. 8.3 - In Exercises 17 to 30, use the formula A=12aP to...Ch. 8.3 - Find the shaded area if the a triangles are...Ch. 8.3 - In terms of the apothem a and length of side s of...Ch. 8.3 - Find the ratio of the area of a square...Ch. 8.3 - Given regular hexagon ABCDEF with each side of the...Ch. 8.3 - Given a regular octagon RSTUVWXY with each side of...Ch. 8.3 - Regular octagon ABCDEFGH is inscribed in a circle...Ch. 8.3 - Given regular pentagon RSTVQ and equilateral...Ch. 8.3 - Consider regular pentagon RSTVQ not shown. Given...Ch. 8.3 - Consider a regular hexagon ABCDEF not shown. By...Ch. 8.3 - The length of each side of a regular hexagon...Ch. 8.3 - For equilateral ARST, RT = 6. Squares and...Ch. 8.3 - For square MNPQ, MN = 4. Congruent squares and...Ch. 8.4 - Find the exact circumference and area of a circle...Ch. 8.4 - Find the exact circumference and area of a circle...Ch. 8.4 - Prob. 3ECh. 8.4 - Find the approximate circumference and area of a...Ch. 8.4 - Find the exact lengths of the radius and the...Ch. 8.4 - Find the approximate lengths of the radius and the...Ch. 8.4 - Find the exact lengths of the radius and the...Ch. 8.4 - Find the exact length of the radius and the exact...Ch. 8.4 - Find the exact length of AB, where AB refers to...Ch. 8.4 - Find the exact length of minor arc CD.Ch. 8.4 - Prob. 11ECh. 8.4 - Prob. 12ECh. 8.4 - A metal circular disk whose area is 143 cm2 is...Ch. 8.4 - Prob. 14ECh. 8.4 - The central angle corresponding to a circular...Ch. 8.4 - Use your calculator to find, to two decimal places...Ch. 8.4 - Prob. 17ECh. 8.4 - A rectangle has an area of 36 in2. What is the...Ch. 8.4 - The legs of an isosceles triangle each measure 10...Ch. 8.4 - Two sides of a triangle measure 5 in and 7 in....Ch. 8.4 - Let N be any point on side BC of the right...Ch. 8.4 - What is the limit of mRTS if T lies in the...Ch. 8.4 - In exercises 23-26, find the exact areas of shaded...Ch. 8.4 - In exercises 23-26, find the exact areas of shaded...Ch. 8.4 - In exercises 23-26, find the exact areas of shaded...Ch. 8.4 - In exercises 23-26, find the exact areas of the...Ch. 8.4 - In Exercises 27 and 28, use your calculator value...Ch. 8.4 - Prob. 28ECh. 8.4 - Prob. 29ECh. 8.4 - The ratio of the circumferences of two circles is...Ch. 8.4 - Given concentric circles with radii of lengths R...Ch. 8.4 - Prob. 32ECh. 8.4 - The radii of two concentric circles differ in...Ch. 8.4 - Prob. 34ECh. 8.4 - In exercises 34-45, use your calculator value of ...Ch. 8.4 - Prob. 36ECh. 8.4 - Prob. 37ECh. 8.4 - In exercises 34-45, use your calculator value of ...Ch. 8.4 - Prob. 39ECh. 8.4 - Prob. 40ECh. 8.4 - Prob. 41ECh. 8.4 - Prob. 42ECh. 8.4 - In exercises 34-45, use your calculator value of ...Ch. 8.4 - In exercises 34-45, use your calculator value of ...Ch. 8.4 - In exercises 34-45, use your calculator value of ...Ch. 8.4 - A tabletop is semicircular when its three...Ch. 8.4 - Given that the length of each side of a rhombus is...Ch. 8.4 - A circle has a radius length of 5.3 cm. Find the...Ch. 8.4 - A square has a length of 8.9 in for each side....Ch. 8.5 - Given O with radii OA- and OB- and chord AB-....Ch. 8.5 - Prob. 2ECh. 8.5 - In the semicircular region shaded DQ=6". a Find...Ch. 8.5 - For the semicircular region of Exercise 3, the...Ch. 8.5 - In the circle, the radius length is 10 in. and the...Ch. 8.5 - If the area of the circle is 360 in2, what is the...Ch. 8.5 - If the area of 1200 sector is 50 cm2, what is the...Ch. 8.5 - If the area of the 1200 sector is 40 cm2 and the...Ch. 8.5 - Prob. 9ECh. 8.5 - Suppose a circle of radius r is inscribed in a...Ch. 8.5 - Find the perimeter of a segment of a circle whose...Ch. 8.5 - Prob. 12ECh. 8.5 - A circle is inscribed in a triangle having sides...Ch. 8.5 - A circle is inscribed in a triangle having sides...Ch. 8.5 - A triangle with sides of lengths 3 in., 4 in., and...Ch. 8.5 - The approximate area of a triangle with sides of...Ch. 8.5 - Find the exact perimeter and area of the sector...Ch. 8.5 - Find the exact perimeter and area of the sector...Ch. 8.5 - Prob. 19ECh. 8.5 - Find the approximate area of the sector shown....Ch. 8.5 - Find the exact perimeter and area of the segment...Ch. 8.5 - Prob. 22ECh. 8.5 - In Exercises 23 and 24, find the exact areas of...Ch. 8.5 - In Exercises 23 and 24, find the exact areas of...Ch. 8.5 - Assuming that the exact area of a sector...Ch. 8.5 - Prob. 26ECh. 8.5 - A circle can be inscribed in the trapezoid shown....Ch. 8.5 - Prob. 28ECh. 8.5 - In a circle whose radius has length 12 m, the...Ch. 8.5 - At the Pizza Dude restaurant, a 12-in. pizza costs...Ch. 8.5 - Prob. 31ECh. 8.5 - Determine a formula for the area of the shaded...Ch. 8.5 - Determine a formula for the area of the shaded...Ch. 8.5 - Find a formula for the area of the shaded region,...Ch. 8.5 - A company logo on the side of a building shows an...Ch. 8.5 - Prob. 36ECh. 8.5 - Prob. 37ECh. 8.5 - Use the results from Exercises 36 and 37 to find...Ch. 8.5 - Prob. 39ECh. 8.5 - Three pipes, each of radius length 4 in., are...Ch. 8.5 - In Exercises 41 and 42, round to two decimal...Ch. 8.5 - In Exercises 41 and 42, round to two decimal...Ch. 8.5 - An exit ramp from one freeway to another freeway...Ch. 8.5 - In ABC,mC=90 and mB=60. If AB=12 in., find the...Ch. 8.5 - A triangle has sides of lengths 6 cm, 8 cm and 10...Ch. 8.CR - For the Review Exercises, give an exact answer...Ch. 8.CR - For the Review Exercises, give an exact answer...Ch. 8.CR - Prob. 3CRCh. 8.CR - Prob. 4CRCh. 8.CR - Prob. 5CRCh. 8.CR - Given: Trapezoid ABCD, with...Ch. 8.CR - Given: Trapezoid ABCD, with AB=6andBC=8,ABCD Find:...Ch. 8.CR - Find the area and the perimeter of a rhombus whose...Ch. 8.CR - Tom Morrow wants to buy some fertilizer for his...Ch. 8.CR - Alices mother wants to wallpaper two adjacent...Ch. 8.CR - Given: Isosceles trapezoid ABCD Equilateral FBC...Ch. 8.CR - Given: Kite ABCD withAB=10BC=17,andBD=16 Find:...Ch. 8.CR - One side of a rectangle is 2 cm longer than a...Ch. 8.CR - One side of a triangle is 10 cm longer than a...Ch. 8.CR - Prob. 15CRCh. 8.CR - Find the area of an equilateral triangle if each...Ch. 8.CR - If AC is a diameter of O, find the area of the...Ch. 8.CR - Prob. 18CRCh. 8.CR - Find the area of a regular hexagon, each of whose...Ch. 8.CR - Prob. 20CRCh. 8.CR - Prob. 21CRCh. 8.CR - Prob. 22CRCh. 8.CR - Can a circle be circumscribed about each of the...Ch. 8.CR - Can a circle be inscribed in each of the following...Ch. 8.CR - Prob. 25CRCh. 8.CR - The Turners want to install outdoor carpet around...Ch. 8.CR - Find the exact areas of the shaded regions in...Ch. 8.CR - Find the exact areas of the shaded regions in...Ch. 8.CR - Find the exact areas of the shaded regions in...Ch. 8.CR - Find the exact areas of the shaded regions in...Ch. 8.CR - Find the exact areas of the shaded regions in...Ch. 8.CR - The arc of a sector measures 40. Find the exact...Ch. 8.CR - The circumference of a circle is 66 ft. aFind the...Ch. 8.CR - A circle has an exact area of 27ft2. aWhat is the...Ch. 8.CR - Prob. 35CRCh. 8.CR - Prob. 36CRCh. 8.CR - Prove that the area of a circle circumscribed...Ch. 8.CR - Prove that if semicircles are constructed on each...Ch. 8.CR - Jeff and Helen want to carpet their family room,...Ch. 8.CR - Sue and Daves semicircular driveway is to be...Ch. 8.CR - Prob. 41CRCh. 8.CT - Complete each statement. a Given that the length...Ch. 8.CT - Give each formula. a The formula for the area of a...Ch. 8.CT - Prob. 3CTCh. 8.CT - If the area of rectangle ABCD is 46 cm2, find the...Ch. 8.CT - Prob. 5CTCh. 8.CT - Find the area of rhombus MNPQ given that QN=8 ft...Ch. 8.CT - Prob. 7CTCh. 8.CT - Prob. 8CTCh. 8.CT - Prob. 9CTCh. 8.CT - For the circle shown below, the length of the...Ch. 8.CT - Prob. 11CTCh. 8.CT - Prob. 12CTCh. 8.CT - In the figure, a square is inscribed in a circle....Ch. 8.CT - Prob. 14CTCh. 8.CT - Find the exact area of the shaded segment.Ch. 8.CT - Prob. 16CTCh. 8.CT - Pascual is remodeling a house and plans a complete...
Additional Math Textbook Solutions
Find more solutions based on key concepts
To identify the solid.
Geometry, Student Edition
The measure of third arc from the help of given information.
McDougal Littell Jurgensen Geometry: Student Edition Geometry
The possible names of the line containing the points.
Geometry For Enjoyment And Challenge
For each hour of class time, how many hours outside of class are recommended for studying and doing homework?
Elementary Algebra For College Students (9th Edition)
Let S be the parallelogram determined by the vectors b1 = [13] and b2 = [51], and let A = [1102]. Compute the a...
Linear Algebra and Its Applications (5th Edition)
153. A rain gutter is made from sheets of aluminum that are 20 inches wide. As shown in the figure, the edges ...
College Algebra (7th Edition)
Knowledge Booster
Learn more about
Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, geometry and related others by exploring similar questions and additional content below.Similar questions
- In Exercises 27 to 30, find the area of the figure shown. Given: Pentagon RSTVW with mVRS=mVSR=60,RS=82, and RW-WV-VT-TS- Find: ARSTVWarrow_forwardIn Exercises 5 to 10, the real numbers a, b, c, and d are positive. Consider the quadrilateral with vertices at A0,0, Ba,0, Cb,c, and Dd,c. Explain why ABCD is a trapezoid.arrow_forwardIn concave quadrilateral ABCD, the angle at A measures 40. ABD is isosceles, BC bisects ABD, and DC bisects ADB. What are the measures of ABC, ADC, and 1?arrow_forward
- In Exercises 9 to 28, use the drawings as needed to answer the following questions. Explain the difference, if any, between a CDandDC. c CDandDC. b CDandDC. d CDandDC.arrow_forwardIn Exercises 9 to 28, use the drawings as needed to answer the following questions. Consider the figure for Exercise 27. Given that B is the midpoint of AC and C is the midpoint of BD, what can you conclude about the lengths of a ABandCD? c ACandCD? b ACandBD? Exercises 27, 28arrow_forwardIn Exercises 39 to 47, provide a paragraph proof. Be sure to provide a drawing, Given, and Prove where needed. If a parallelogram is inscribed in a circle, then it is a rectangle.arrow_forward
- In Exercises 27 to 30, find the area of the figure shown. Given: Hexagon RSTVWX with WV-XT-RS- RS=10 ST=8 TV=5 WV=16 WX-VT- Find: ARSTVWXarrow_forwardUse the results from Exercises 36 and 37 to find the exact length of the radius of the inscribed circle for a triangle with sides of lengths a 8, 15 and 17 b 7, 9 and 12arrow_forwardIn Review Exercises 4 to 6, name the type of reasoning illustrated. While watching the pitcher warm up, Phillip thinks, Ill be able to hit against him.arrow_forward
- In ABC, M is the midpoint of AB and N is the midpoint of AC. If MN= 3x-11 and BC= 4x24, find the value of x._arrow_forwardIn Exercises 29 to 31, M and Nare the midpoints of sides RS and RT ofRST, respectively. Given: RM=RN=2x+1 ST=5x-3 mR=60 Find: x, RM, and STarrow_forwardIn Exercises 15 to 18, describe the triangle XYZ , not shown as scalene, isosceles, or equilateral. Also, is the triangle acute, right, or obtuse? mX=60 and YZarrow_forward
arrow_back_ios
SEE MORE QUESTIONS
arrow_forward_ios
Recommended textbooks for you
 Elementary Geometry For College Students, 7eGeometryISBN:9781337614085Author:Alexander, Daniel C.; Koeberlein, Geralyn M.Publisher:Cengage,
Elementary Geometry For College Students, 7eGeometryISBN:9781337614085Author:Alexander, Daniel C.; Koeberlein, Geralyn M.Publisher:Cengage, Holt Mcdougal Larson Pre-algebra: Student Edition...AlgebraISBN:9780547587776Author:HOLT MCDOUGALPublisher:HOLT MCDOUGAL
Holt Mcdougal Larson Pre-algebra: Student Edition...AlgebraISBN:9780547587776Author:HOLT MCDOUGALPublisher:HOLT MCDOUGAL Elementary Geometry for College StudentsGeometryISBN:9781285195698Author:Daniel C. Alexander, Geralyn M. KoeberleinPublisher:Cengage Learning
Elementary Geometry for College StudentsGeometryISBN:9781285195698Author:Daniel C. Alexander, Geralyn M. KoeberleinPublisher:Cengage Learning

Elementary Geometry For College Students, 7e
Geometry
ISBN:9781337614085
Author:Alexander, Daniel C.; Koeberlein, Geralyn M.
Publisher:Cengage,

Holt Mcdougal Larson Pre-algebra: Student Edition...
Algebra
ISBN:9780547587776
Author:HOLT MCDOUGAL
Publisher:HOLT MCDOUGAL

Elementary Geometry for College Students
Geometry
ISBN:9781285195698
Author:Daniel C. Alexander, Geralyn M. Koeberlein
Publisher:Cengage Learning
An Introduction to Area | Teaching Maths | EasyTeaching; Author: EasyTeaching;https://www.youtube.com/watch?v=_uKKl8R1xBM;License: Standard YouTube License, CC-BY
Area of a Rectangle, Triangle, Circle & Sector, Trapezoid, Square, Parallelogram, Rhombus, Geometry; Author: The Organic Chemistry Tutor;https://www.youtube.com/watch?v=JnLDmw3bbuw;License: Standard YouTube License, CC-BY