
Elementary Geometry For College Students, 7e
7th Edition
ISBN: 9781337614085
Author: Alexander, Daniel C.; Koeberlein, Geralyn M.
Publisher: Cengage,
expand_more
expand_more
format_list_bulleted
Textbook Question
Chapter 8.3, Problem 32E
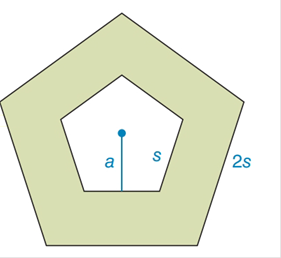
In terms of the apothem
Expert Solution & Answer
Want to see the full answer?
Check out a sample textbook solution
Chapter 8 Solutions
Elementary Geometry For College Students, 7e
Ch. 8.1 - Suppose that two triangles have equal areas. Are...Ch. 8.1 - The area of the square is 12, and the area of the...Ch. 8.1 - Consider the information in Exercise 2, but...Ch. 8.1 - If MNPQ is a rhombus, which formula from this...Ch. 8.1 - In rhombus MNPQ, how does the length of the...Ch. 8.1 - When the diagonals of rhombus MNPQ are drawn, how...Ch. 8.1 - Prob. 7ECh. 8.1 - Are ABC and DEF congruent? Exercises 7, 8Ch. 8.1 - Prob. 9ECh. 8.1 - In Exercises 9 to 18, find the areas of the...
Ch. 8.1 - In Exercises 9 to 18, find the areas of the...Ch. 8.1 - Prob. 12ECh. 8.1 - In Exercises 9 to 18, find the areas of the...Ch. 8.1 - In Exercises 9 to 18, find the areas of the...Ch. 8.1 - In Exercises 9 to 18, find the areas of the...Ch. 8.1 - In Exercises 9 to 18, find the areas of the...Ch. 8.1 - In Exercises 9 to 18, find the areas of the...Ch. 8.1 - Prob. 18ECh. 8.1 - In Exercises 19 to 22, find the area of the shaded...Ch. 8.1 - Prob. 20ECh. 8.1 - In Exercises 19 to 22, find the area of the shaded...Ch. 8.1 - In Exercises 19 to 22, find the area of the shaded...Ch. 8.1 - A triangular corner of a store has been roped off...Ch. 8.1 - Carpeting is to be purchased for the family room...Ch. 8.1 - The exterior wall the gabled end of the house...Ch. 8.1 - The roof of the house shown needs to be...Ch. 8.1 - A beach tent is designed so that one side is open....Ch. 8.1 - Gary and Carolyn plan to build the deck shown. a...Ch. 8.1 - A square yard is a square with sides 1 yard in...Ch. 8.1 - The following problem is based on this theorem: A...Ch. 8.1 - For Exercise 31 and 32, X is the midpoint of VT...Ch. 8.1 - Prob. 32ECh. 8.1 - Prob. 33ECh. 8.1 - In Exercises 34 to 36, provide paragraph proofs....Ch. 8.1 - In Exercises 34 to 36, provide paragraph proofs....Ch. 8.1 - In Exercises 34 to 36, provide paragraph proofs....Ch. 8.1 - Given: The area of right ABC not shown is 40in2....Ch. 8.1 - The lengths of the legs of a right triangle are...Ch. 8.1 - Given: ABC, whose sides are 13 in., 14 in., and 15...Ch. 8.1 - Prob. 40ECh. 8.1 - If the length of the base of a rectangle is...Ch. 8.1 - If the length of the base of a rectangle is...Ch. 8.1 - Prob. 43ECh. 8.1 - Prob. 44ECh. 8.1 - The algebra method of FOIL multiplication is...Ch. 8.1 - Use the square configuration to complete the...Ch. 8.1 - In Exercises 47 to 50, use the fact that the area...Ch. 8.1 - Prob. 48ECh. 8.1 - Prob. 49ECh. 8.1 - In Exercises 47 to 50, use the fact that the area...Ch. 8.1 - The area of a rectangle is 48in2. Where x is the...Ch. 8.1 - The perimeter of the rectangle is 32 cm. Where x...Ch. 8.1 - Square DEFG is inscribed in right ABC, as shown....Ch. 8.1 - TV bisects STR of STR. ST=6 and TR=9. If the area...Ch. 8.1 - Prob. 55ECh. 8.1 - Prob. 56ECh. 8.2 - In Exercises 1 to 8, find the perimeter of each...Ch. 8.2 - In Exercises 1 to 8, find the perimeter of each...Ch. 8.2 - In Exercises 1 to 8, find the perimeter of each...Ch. 8.2 - In Exercises 1 to 8, find the perimeter of each...Ch. 8.2 - In Exercises 1 to 8, find the perimeter of each...Ch. 8.2 - In Exercises 1 to 8, find the perimeter of each...Ch. 8.2 - In Exercises 1 to 8, find the perimeter of each...Ch. 8.2 - In Exercises 1 to 8, find the perimeter of each...Ch. 8.2 - In Exercises 9 and 10, use Herons Formula. Find...Ch. 8.2 - Prob. 10ECh. 8.2 - For Exercises 11 and 12, use Brahmaguptas Formula....Ch. 8.2 - For Exercises 11 and 12, use Brahmaguptas Formula....Ch. 8.2 - In Exercises 13 to 18, find the area of the given...Ch. 8.2 - In Exercises 13 to 18, find the area of the given...Ch. 8.2 - In Exercises 13 to 18, find the area of the given...Ch. 8.2 - Prob. 16ECh. 8.2 - Prob. 17ECh. 8.2 - In Exercises 13 to 18, find the area of the given...Ch. 8.2 - In a triangle of perimeter 76 in., the length of...Ch. 8.2 - In a triangle whose area is 72 in2, the base has a...Ch. 8.2 - A trapezoid has an area of 96 cm2. If the altitude...Ch. 8.2 - The numerical difference between the area of a...Ch. 8.2 - Prob. 23ECh. 8.2 - Find the ratio A1A2 of the areas of two similar...Ch. 8.2 - In Exercises 25 and 26, give a paragraph form of...Ch. 8.2 - In Exercises 25 and 26, give a paragraph form of...Ch. 8.2 - In Exercises 27 to 30, find the area of the figure...Ch. 8.2 - In Exercises 27 to 30, find the area of the figure...Ch. 8.2 - In Exercises 27 to 30, find the area of the figure...Ch. 8.2 - In Exercises 27 to 30, find the area of the figure...Ch. 8.2 - Mary Frances has a rectangular garden plot that...Ch. 8.2 - Prob. 32ECh. 8.2 - Farmer Watson wishes to fence a rectangular plot...Ch. 8.2 - The farmer in Exercise 33 has decided to take the...Ch. 8.2 - Prob. 35ECh. 8.2 - Find the perimeter of the room in Exercise 35.Ch. 8.2 - Examine several rectangles, each with a perimeter...Ch. 8.2 - Examine several rectangles, each with an area of...Ch. 8.2 - Square RSTV is inscribed in square WXYZ, as shown....Ch. 8.2 - Square RSTV is inscribed in square WXYZ, as shown....Ch. 8.2 - For Exercises 41 and 42, the sides of square ABCD...Ch. 8.2 - For Exercises 41 and 42, the sides of square ABCD...Ch. 8.2 - Prob. 43ECh. 8.2 - Prob. 44ECh. 8.2 - For Exercises 45 and 46, use this information: Let...Ch. 8.2 - Prob. 46ECh. 8.2 - Prob. 47ECh. 8.2 - Prob. 48ECh. 8.2 - For Exercises 48 and 49, use the formula found in...Ch. 8.2 - Prove that the area of a square whose diagonal has...Ch. 8.2 - Prob. 51ECh. 8.2 - Prob. 52ECh. 8.2 - The shaded region is that of a trapezoid....Ch. 8.2 - Trapezoid ABCD not shown is inscribed in O so that...Ch. 8.2 - Each side of square RSTV has length 8. Point W...Ch. 8.2 - For the cyclic quadrilateral MNPQ, the sides have...Ch. 8.2 - Prob. 57ECh. 8.3 - Find the area of a square with a sides of length...Ch. 8.3 - Find the area of a square with a a perimeter of...Ch. 8.3 - Find the area of an equilateral triangle with a...Ch. 8.3 - Find the area of an equiangular triangle with a a...Ch. 8.3 - In a regular polygon, each central angle measures...Ch. 8.3 - In a regular polygon, each interior angle measures...Ch. 8.3 - For a regular hexagon, the length of the apothem...Ch. 8.3 - For a regular hexagon, the length of the radius is...Ch. 8.3 - In a particular type of regular polygon, the...Ch. 8.3 - In a particular type of regular polygon, the...Ch. 8.3 - Prob. 11ECh. 8.3 - If the area (A=12aP) and the perimeter of a...Ch. 8.3 - Find the area of a square with apothem a = 3.2 cm...Ch. 8.3 - Find the area of an equilateral triangle with...Ch. 8.3 - Find the area of an equilateral triangle with...Ch. 8.3 - Find the area of a square with apothem a = 8.2 ft...Ch. 8.3 - In Exercises 17 to 30, use the formula A=12aP to...Ch. 8.3 - In Exercises 17 to 30, use the formula A=12aP to...Ch. 8.3 - In Exercises 17 to 30, use the formula A=12aP to...Ch. 8.3 - In Exercises 17 to 30, use the formula A=12aP to...Ch. 8.3 - Prob. 21ECh. 8.3 - In Exercises 17 to 30, use the formula A=12aP to...Ch. 8.3 - In Exercises 17 to 30, use the formula A=12aP to...Ch. 8.3 - In Exercises 17 to 30, use the formula A=12aP to...Ch. 8.3 - In Exercises 17 to 30, use the formula A=12aP to...Ch. 8.3 - In Exercises 17 to 30, use the formula A=12aP to...Ch. 8.3 - In Exercises 17 to 30, use the formula A=12aP to...Ch. 8.3 - In Exercises 17 to 30, use the formula A=12aP to...Ch. 8.3 - In Exercises 17 to 30, use the formula A=12aP to...Ch. 8.3 - In Exercises 17 to 30, use the formula A=12aP to...Ch. 8.3 - Find the shaded area if the a triangles are...Ch. 8.3 - In terms of the apothem a and length of side s of...Ch. 8.3 - Find the ratio of the area of a square...Ch. 8.3 - Given regular hexagon ABCDEF with each side of the...Ch. 8.3 - Given a regular octagon RSTUVWXY with each side of...Ch. 8.3 - Regular octagon ABCDEFGH is inscribed in a circle...Ch. 8.3 - Given regular pentagon RSTVQ and equilateral...Ch. 8.3 - Consider regular pentagon RSTVQ not shown. Given...Ch. 8.3 - Consider a regular hexagon ABCDEF not shown. By...Ch. 8.3 - The length of each side of a regular hexagon...Ch. 8.3 - For equilateral ARST, RT = 6. Squares and...Ch. 8.3 - For square MNPQ, MN = 4. Congruent squares and...Ch. 8.4 - Find the exact circumference and area of a circle...Ch. 8.4 - Find the exact circumference and area of a circle...Ch. 8.4 - Prob. 3ECh. 8.4 - Find the approximate circumference and area of a...Ch. 8.4 - Find the exact lengths of the radius and the...Ch. 8.4 - Find the approximate lengths of the radius and the...Ch. 8.4 - Find the exact lengths of the radius and the...Ch. 8.4 - Find the exact length of the radius and the exact...Ch. 8.4 - Find the exact length of AB, where AB refers to...Ch. 8.4 - Find the exact length of minor arc CD.Ch. 8.4 - Prob. 11ECh. 8.4 - Prob. 12ECh. 8.4 - A metal circular disk whose area is 143 cm2 is...Ch. 8.4 - Prob. 14ECh. 8.4 - The central angle corresponding to a circular...Ch. 8.4 - Use your calculator to find, to two decimal places...Ch. 8.4 - Prob. 17ECh. 8.4 - A rectangle has an area of 36 in2. What is the...Ch. 8.4 - The legs of an isosceles triangle each measure 10...Ch. 8.4 - Two sides of a triangle measure 5 in and 7 in....Ch. 8.4 - Let N be any point on side BC of the right...Ch. 8.4 - What is the limit of mRTS if T lies in the...Ch. 8.4 - In exercises 23-26, find the exact areas of shaded...Ch. 8.4 - In exercises 23-26, find the exact areas of shaded...Ch. 8.4 - In exercises 23-26, find the exact areas of shaded...Ch. 8.4 - In exercises 23-26, find the exact areas of the...Ch. 8.4 - In Exercises 27 and 28, use your calculator value...Ch. 8.4 - Prob. 28ECh. 8.4 - Prob. 29ECh. 8.4 - The ratio of the circumferences of two circles is...Ch. 8.4 - Given concentric circles with radii of lengths R...Ch. 8.4 - Prob. 32ECh. 8.4 - The radii of two concentric circles differ in...Ch. 8.4 - Prob. 34ECh. 8.4 - In exercises 34-45, use your calculator value of ...Ch. 8.4 - Prob. 36ECh. 8.4 - Prob. 37ECh. 8.4 - In exercises 34-45, use your calculator value of ...Ch. 8.4 - Prob. 39ECh. 8.4 - Prob. 40ECh. 8.4 - Prob. 41ECh. 8.4 - Prob. 42ECh. 8.4 - In exercises 34-45, use your calculator value of ...Ch. 8.4 - In exercises 34-45, use your calculator value of ...Ch. 8.4 - In exercises 34-45, use your calculator value of ...Ch. 8.4 - A tabletop is semicircular when its three...Ch. 8.4 - Given that the length of each side of a rhombus is...Ch. 8.4 - A circle has a radius length of 5.3 cm. Find the...Ch. 8.4 - A square has a length of 8.9 in for each side....Ch. 8.5 - Given O with radii OA- and OB- and chord AB-....Ch. 8.5 - Prob. 2ECh. 8.5 - In the semicircular region shaded DQ=6". a Find...Ch. 8.5 - For the semicircular region of Exercise 3, the...Ch. 8.5 - In the circle, the radius length is 10 in. and the...Ch. 8.5 - If the area of the circle is 360 in2, what is the...Ch. 8.5 - If the area of 1200 sector is 50 cm2, what is the...Ch. 8.5 - If the area of the 1200 sector is 40 cm2 and the...Ch. 8.5 - Prob. 9ECh. 8.5 - Suppose a circle of radius r is inscribed in a...Ch. 8.5 - Find the perimeter of a segment of a circle whose...Ch. 8.5 - Prob. 12ECh. 8.5 - A circle is inscribed in a triangle having sides...Ch. 8.5 - A circle is inscribed in a triangle having sides...Ch. 8.5 - A triangle with sides of lengths 3 in., 4 in., and...Ch. 8.5 - The approximate area of a triangle with sides of...Ch. 8.5 - Find the exact perimeter and area of the sector...Ch. 8.5 - Find the exact perimeter and area of the sector...Ch. 8.5 - Prob. 19ECh. 8.5 - Find the approximate area of the sector shown....Ch. 8.5 - Find the exact perimeter and area of the segment...Ch. 8.5 - Prob. 22ECh. 8.5 - In Exercises 23 and 24, find the exact areas of...Ch. 8.5 - In Exercises 23 and 24, find the exact areas of...Ch. 8.5 - Assuming that the exact area of a sector...Ch. 8.5 - Prob. 26ECh. 8.5 - A circle can be inscribed in the trapezoid shown....Ch. 8.5 - Prob. 28ECh. 8.5 - In a circle whose radius has length 12 m, the...Ch. 8.5 - At the Pizza Dude restaurant, a 12-in. pizza costs...Ch. 8.5 - Prob. 31ECh. 8.5 - Determine a formula for the area of the shaded...Ch. 8.5 - Determine a formula for the area of the shaded...Ch. 8.5 - Find a formula for the area of the shaded region,...Ch. 8.5 - A company logo on the side of a building shows an...Ch. 8.5 - Prob. 36ECh. 8.5 - Prob. 37ECh. 8.5 - Use the results from Exercises 36 and 37 to find...Ch. 8.5 - Prob. 39ECh. 8.5 - Three pipes, each of radius length 4 in., are...Ch. 8.5 - In Exercises 41 and 42, round to two decimal...Ch. 8.5 - In Exercises 41 and 42, round to two decimal...Ch. 8.5 - An exit ramp from one freeway to another freeway...Ch. 8.5 - In ABC,mC=90 and mB=60. If AB=12 in., find the...Ch. 8.5 - A triangle has sides of lengths 6 cm, 8 cm and 10...Ch. 8.CR - For the Review Exercises, give an exact answer...Ch. 8.CR - For the Review Exercises, give an exact answer...Ch. 8.CR - Prob. 3CRCh. 8.CR - Prob. 4CRCh. 8.CR - Prob. 5CRCh. 8.CR - Given: Trapezoid ABCD, with...Ch. 8.CR - Given: Trapezoid ABCD, with AB=6andBC=8,ABCD Find:...Ch. 8.CR - Find the area and the perimeter of a rhombus whose...Ch. 8.CR - Tom Morrow wants to buy some fertilizer for his...Ch. 8.CR - Alices mother wants to wallpaper two adjacent...Ch. 8.CR - Given: Isosceles trapezoid ABCD Equilateral FBC...Ch. 8.CR - Given: Kite ABCD withAB=10BC=17,andBD=16 Find:...Ch. 8.CR - One side of a rectangle is 2 cm longer than a...Ch. 8.CR - One side of a triangle is 10 cm longer than a...Ch. 8.CR - Prob. 15CRCh. 8.CR - Find the area of an equilateral triangle if each...Ch. 8.CR - If AC is a diameter of O, find the area of the...Ch. 8.CR - Prob. 18CRCh. 8.CR - Find the area of a regular hexagon, each of whose...Ch. 8.CR - Prob. 20CRCh. 8.CR - Prob. 21CRCh. 8.CR - Prob. 22CRCh. 8.CR - Can a circle be circumscribed about each of the...Ch. 8.CR - Can a circle be inscribed in each of the following...Ch. 8.CR - Prob. 25CRCh. 8.CR - The Turners want to install outdoor carpet around...Ch. 8.CR - Find the exact areas of the shaded regions in...Ch. 8.CR - Find the exact areas of the shaded regions in...Ch. 8.CR - Find the exact areas of the shaded regions in...Ch. 8.CR - Find the exact areas of the shaded regions in...Ch. 8.CR - Find the exact areas of the shaded regions in...Ch. 8.CR - The arc of a sector measures 40. Find the exact...Ch. 8.CR - The circumference of a circle is 66 ft. aFind the...Ch. 8.CR - A circle has an exact area of 27ft2. aWhat is the...Ch. 8.CR - Prob. 35CRCh. 8.CR - Prob. 36CRCh. 8.CR - Prove that the area of a circle circumscribed...Ch. 8.CR - Prove that if semicircles are constructed on each...Ch. 8.CR - Jeff and Helen want to carpet their family room,...Ch. 8.CR - Sue and Daves semicircular driveway is to be...Ch. 8.CR - Prob. 41CRCh. 8.CT - Complete each statement. a Given that the length...Ch. 8.CT - Give each formula. a The formula for the area of a...Ch. 8.CT - Prob. 3CTCh. 8.CT - If the area of rectangle ABCD is 46 cm2, find the...Ch. 8.CT - Prob. 5CTCh. 8.CT - Find the area of rhombus MNPQ given that QN=8 ft...Ch. 8.CT - Prob. 7CTCh. 8.CT - Prob. 8CTCh. 8.CT - Prob. 9CTCh. 8.CT - For the circle shown below, the length of the...Ch. 8.CT - Prob. 11CTCh. 8.CT - Prob. 12CTCh. 8.CT - In the figure, a square is inscribed in a circle....Ch. 8.CT - Prob. 14CTCh. 8.CT - Find the exact area of the shaded segment.Ch. 8.CT - Prob. 16CTCh. 8.CT - Pascual is remodeling a house and plans a complete...
Knowledge Booster
Learn more about
Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, geometry and related others by exploring similar questions and additional content below.Similar questions
- Find the lengths of the apothem and the radius of a square whose sides have length 10 in.arrow_forwardIn a particular type of regular polygon, the length of the apothem is exactly one-half the length of a side. What type of regular polygon is it?arrow_forwardFind the lengths of the side and the radius of a regular hexagon whose apothem has the length 10 m.arrow_forward
- Find the lengths of the apothem and the radius of a regular hexagon whose sides have length 6 cm.arrow_forwardIf the area (A=12aP) and the perimeter of a regular polygon are numerically equal, find the length of the apothem of the regular polygon.arrow_forwardWhich of these two polyhedrons is concave? Note that the interior dihedral angle formed by the planes containing EJF and KJF is larger than 180 .arrow_forward
- A circle is inscribed in an isosceles triangle with legs of length 10 in. and a base of length 12 in. Find the length of the radius of the inscribed circle.arrow_forwardIn the illustration, point M is the midpoint of the hypotenuse of right triangle AOB. Show that the area of rectangle OLMN is one-half of the area of triangle AOB.arrow_forwardThe radii of two concentric circles differ in length by exactly 1 in. If their areas differ by exactly 7 in2, find the lengths of the radii of the two circles.arrow_forward
arrow_back_ios
arrow_forward_ios
Recommended textbooks for you
 Elementary Geometry For College Students, 7eGeometryISBN:9781337614085Author:Alexander, Daniel C.; Koeberlein, Geralyn M.Publisher:Cengage,
Elementary Geometry For College Students, 7eGeometryISBN:9781337614085Author:Alexander, Daniel C.; Koeberlein, Geralyn M.Publisher:Cengage, College Algebra (MindTap Course List)AlgebraISBN:9781305652231Author:R. David Gustafson, Jeff HughesPublisher:Cengage Learning
College Algebra (MindTap Course List)AlgebraISBN:9781305652231Author:R. David Gustafson, Jeff HughesPublisher:Cengage Learning Elementary Geometry for College StudentsGeometryISBN:9781285195698Author:Daniel C. Alexander, Geralyn M. KoeberleinPublisher:Cengage Learning
Elementary Geometry for College StudentsGeometryISBN:9781285195698Author:Daniel C. Alexander, Geralyn M. KoeberleinPublisher:Cengage Learning Holt Mcdougal Larson Pre-algebra: Student Edition...AlgebraISBN:9780547587776Author:HOLT MCDOUGALPublisher:HOLT MCDOUGAL
Holt Mcdougal Larson Pre-algebra: Student Edition...AlgebraISBN:9780547587776Author:HOLT MCDOUGALPublisher:HOLT MCDOUGAL

Elementary Geometry For College Students, 7e
Geometry
ISBN:9781337614085
Author:Alexander, Daniel C.; Koeberlein, Geralyn M.
Publisher:Cengage,

College Algebra (MindTap Course List)
Algebra
ISBN:9781305652231
Author:R. David Gustafson, Jeff Hughes
Publisher:Cengage Learning

Elementary Geometry for College Students
Geometry
ISBN:9781285195698
Author:Daniel C. Alexander, Geralyn M. Koeberlein
Publisher:Cengage Learning

Holt Mcdougal Larson Pre-algebra: Student Edition...
Algebra
ISBN:9780547587776
Author:HOLT MCDOUGAL
Publisher:HOLT MCDOUGAL
An Introduction to Area | Teaching Maths | EasyTeaching; Author: EasyTeaching;https://www.youtube.com/watch?v=_uKKl8R1xBM;License: Standard YouTube License, CC-BY
Area of a Rectangle, Triangle, Circle & Sector, Trapezoid, Square, Parallelogram, Rhombus, Geometry; Author: The Organic Chemistry Tutor;https://www.youtube.com/watch?v=JnLDmw3bbuw;License: Standard YouTube License, CC-BY