
Calculus: Early Transcendentals
8th Edition
ISBN: 9781285741550
Author: James Stewart
Publisher: Cengage Learning
expand_more
expand_more
format_list_bulleted
Textbook Question
Chapter 16.6, Problem 25E
Find a parametric representation for the surface.
25. The part of the cylinder x2 + y2 + z2 = 36 that lies between the planes z = 0 and z = 3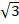
Expert Solution & Answer
Want to see the full answer?
Check out a sample textbook solution
Students have asked these similar questions
Find a parametric representation for the surface S, where S is the part of the cylinder x2+y2 = 4 which lies between the z = −2 and y +z = 2 planes.
Chapter 16 Solutions
Calculus: Early Transcendentals
Ch. 16.1 - Sketch the vector field F by drawing a diagram...Ch. 16.1 - Sketch the vector field F by drawing a diagram...Ch. 16.1 - Sketch the vector field F by drawing a diagram...Ch. 16.1 - Sketch the vector field F by drawing a diagram...Ch. 16.1 - Sketch the vector field F by drawing a diagram...Ch. 16.1 - Sketch the vector field F by drawing a diagram...Ch. 16.1 - Sketch the vector field F by drawing a diagram...Ch. 16.1 - Sketch the vector field F by drawing a diagram...Ch. 16.1 - Sketch the vector field F by drawing a diagram...Ch. 16.1 - Sketch the vector field F by drawing a diagram...
Ch. 16.1 - Match the vector fields F with the plots labeled...Ch. 16.1 - Match the vector fields F with the plots labeled...Ch. 16.1 - Match the vector fields F with the plots labeled...Ch. 16.1 - Match the vector fields F with the plots labeled...Ch. 16.1 - Match the vector fields F on 3 with the plots...Ch. 16.1 - Match the vector fields F on 3 with the plots...Ch. 16.1 - Match the vector fields F on 3 with the plots...Ch. 16.1 - Match the vector fields F on 3 with the plots...Ch. 16.1 - Find the gradient vector field of f. 21. f(x, y) =...Ch. 16.1 - Find the gradient vector field of f. 22. f(s, t) =...Ch. 16.1 - Find the gradient vector field of f. 23. f(x, y,...Ch. 16.1 - Find the gradient vector field of f. 24. f(x, y,...Ch. 16.1 - Find the gradient vector field f of f and sketch...Ch. 16.1 - Find the gradient vector field f of f and sketch...Ch. 16.1 - Match the functions f with the plots of their...Ch. 16.1 - Match the functions f with the plots of their...Ch. 16.1 - Match the functions f with the plots of their...Ch. 16.1 - Match the functions f with the plots of their...Ch. 16.1 - A particle moves in a velocity field V(x, y) = x2,...Ch. 16.1 - At time t = 1, a particle is located at position...Ch. 16.1 - The flow lines (or streamlines) of a vector field...Ch. 16.1 - (a) Sketch the vector field F(x, y) = i + x j and...Ch. 16.2 - Evaluate the line integral, where C is the given...Ch. 16.2 - Evaluate the line integral, where C is the given...Ch. 16.2 - Evaluate the line integral, where C is the given...Ch. 16.2 - Evaluate the line integral, where C is the given...Ch. 16.2 - Evaluate the line integral, where C is the given...Ch. 16.2 - Evaluate the line integral, where C is the given...Ch. 16.2 - Evaluate the line integral, where C is the given...Ch. 16.2 - Evaluate the line integral, where C is the given...Ch. 16.2 - Evaluate the line integral, where C is the given...Ch. 16.2 - Evaluate the line integral, where C is the given...Ch. 16.2 - Evaluate the line integral, where C is the given...Ch. 16.2 - Evaluate the line integral, where C is the given...Ch. 16.2 - Evaluate the line integral, where C is the given...Ch. 16.2 - Evaluate the line integral, where C is the given...Ch. 16.2 - Evaluate the line integral, where C is the given...Ch. 16.2 - Evaluate the line integral, where C is the given...Ch. 16.2 - Let F be the vector field shown in the figure. (a)...Ch. 16.2 - The figure shows a vector field F and two curves...Ch. 16.2 - Prob. 19ECh. 16.2 - Prob. 20ECh. 16.2 - Evaluate the line integral C F dr, where C is...Ch. 16.2 - Evaluate the line integral C F dr, where C is...Ch. 16.2 - Use a calculator to evaluate the line integral...Ch. 16.2 - Use a calculator to evaluate the line integral...Ch. 16.2 - Use a calculator to evaluate the line integral...Ch. 16.2 - Use a calculator to evaluate the line integral...Ch. 16.2 - Prob. 31ECh. 16.2 - (a) Find the work done by the force field F(x, y)...Ch. 16.2 - A thin wire is bent into the shape of a semicircle...Ch. 16.2 - A thin wire has the shape of the first-quadrant...Ch. 16.2 - Prob. 35ECh. 16.2 - Prob. 36ECh. 16.2 - If a wire with linear density (x, y) lies along a...Ch. 16.2 - If a wire with linear density (x, y, z) lies along...Ch. 16.2 - Find the work done by the force field F(x, y) = x...Ch. 16.2 - Find the work done by the force field F(x, y) = x2...Ch. 16.2 - Find the work done by the force field F(x, y, z) =...Ch. 16.2 - The force exerted by an electric charge at the...Ch. 16.2 - The position of an object with mass m at time t is...Ch. 16.2 - Prob. 44ECh. 16.2 - A 160-lb man carries a 25-lb can of paint up a...Ch. 16.2 - Prob. 46ECh. 16.2 - (a) Show that a constant force field does zero...Ch. 16.2 - Prob. 48ECh. 16.2 - Prob. 49ECh. 16.2 - Prob. 50ECh. 16.2 - An object moves along the curve C shown in the...Ch. 16.2 - Experiments show that a steady current I in a long...Ch. 16.3 - The figure shows a curve C and a contour map of a...Ch. 16.3 - A table of values of a function f with continuous...Ch. 16.3 - Determine whether or not F is a conservative...Ch. 16.3 - Determine whether or not F is a conservative...Ch. 16.3 - Determine whether or not F is a conservative...Ch. 16.3 - Determine whether or not F is a conservative...Ch. 16.3 - Determine whether or not F is a conservative...Ch. 16.3 - Determine whether or not F is a conservative...Ch. 16.3 - Determine whether or not F is a conservative...Ch. 16.3 - Determine whether or not F is a conservative...Ch. 16.3 - The figure shows the vector field F(x, y) = 2xy,...Ch. 16.3 - Prob. 12ECh. 16.3 - (a) Find a function f such that F = f and (b) use...Ch. 16.3 - (a) Find a function f such that F = f and (b) use...Ch. 16.3 - (a) Find a function f such that F = f and (b) use...Ch. 16.3 - Prob. 16ECh. 16.3 - Prob. 17ECh. 16.3 - (a) Find a function f such that F = f and (b) use...Ch. 16.3 - Show that the line integral is independent of path...Ch. 16.3 - Show that the line integral is independent of path...Ch. 16.3 - Suppose youre asked to determine the curve that...Ch. 16.3 - Suppose an experiment determines that the amount...Ch. 16.3 - Find the work done by the force field F in moving...Ch. 16.3 - Find the work done by the force field F in moving...Ch. 16.3 - Is the vector field shown in the figure...Ch. 16.3 - Is the vector field shown in the figure...Ch. 16.3 - Let F = f, where f(x, y) = sin(x 2y). Find...Ch. 16.3 - Show that if the vector field F = P i + Q j + R k...Ch. 16.3 - Use Exercise 29 to show that the line integral C y...Ch. 16.3 - Determine whether or not the given set is (a)...Ch. 16.3 - Determine whether or not the given set is (a)...Ch. 16.3 - Prob. 33ECh. 16.3 - Determine whether or not the given set is (a)...Ch. 16.3 - Let F(x, y) = yi+xjx2+y2 (a) Show that P/y=Q/x....Ch. 16.4 - Evaluate the line integral by two methods: (a)...Ch. 16.4 - Evaluate the line integral by two methods: (a)...Ch. 16.4 - Evaluate the line integral by two methods: (a)...Ch. 16.4 - Evaluate the line integral by two methods: (a)...Ch. 16.4 - Use Greens Theorem to evaluate the line integral...Ch. 16.4 - Use Greens Theorem to evaluate the line integral...Ch. 16.4 - Use Greens Theorem to evaluate the line integral...Ch. 16.4 - Use Greens Theorem to evaluate the line integral...Ch. 16.4 - Use Greens Theorem to evaluate the line integral...Ch. 16.4 - Use Greens Theorem to evaluate the line integral...Ch. 16.4 - Use Greens Theorem to evaluate C F dr. (Check the...Ch. 16.4 - Use Greens Theorem to evaluate C F dr. (Check the...Ch. 16.4 - Use Greens Theorem to evaluate C F dr. (Check the...Ch. 16.4 - Use Greens Theorem to evaluate C F dr. (Check the...Ch. 16.4 - Prob. 17ECh. 16.4 - A particle starts at the origin, moves along the...Ch. 16.4 - Use one of the formulas in (5) to find the area...Ch. 16.4 - Prob. 20ECh. 16.4 - (a) If C is the line segment connecting the point...Ch. 16.4 - Let D be a region bounded by a simple closed path...Ch. 16.4 - Use Exercise 22 to find the centroid of a...Ch. 16.4 - Use Exercise 22 to find the centroid of the...Ch. 16.4 - A plane lamina with constant density (x, y) = ...Ch. 16.4 - Prob. 26ECh. 16.4 - Use the method of Example 5 to calculate C F dr,...Ch. 16.4 - Calculate C F dr, where F(x, y) = x2 + y, 3x y2...Ch. 16.4 - If F is the vector field of Example 5, show that C...Ch. 16.4 - Complete the proof of the special case of Greens...Ch. 16.4 - Use Greens Theorem to prove the change of...Ch. 16.5 - Find (a) the curl and (b) the divergence of the...Ch. 16.5 - Find (a) the curl and (b) the divergence of the...Ch. 16.5 - Find (a) the curl and (b) the divergence of the...Ch. 16.5 - Find (a) the curl and (b) the divergence of the...Ch. 16.5 - Find (a) the curl and (b) the divergence of the...Ch. 16.5 - Prob. 6ECh. 16.5 - Find (a) the curl and (b) the divergence of the...Ch. 16.5 - Find (a) the curl and (b) the divergence of the...Ch. 16.5 - The vector field F is shown in the xy-plane and...Ch. 16.5 - The vector field F is shown in the xy-plane and...Ch. 16.5 - The vector field F is shown in the xy-plane and...Ch. 16.5 - Let f be a scalar field and F a vector field....Ch. 16.5 - Determine whether or not the vector field is...Ch. 16.5 - Determine whether or not the vector field is...Ch. 16.5 - Determine whether or not the vector field is...Ch. 16.5 - Determine whether or not the vector field is...Ch. 16.5 - Determine whether or not the vector field is...Ch. 16.5 - Determine whether or not the vector field is...Ch. 16.5 - Is there a vector field G on 3 such that curl G =...Ch. 16.5 - Is there a vector field G on 3 such that curl G =...Ch. 16.5 - Show that any vector field of the form F(x, y, z)...Ch. 16.5 - Show that any vector field of the form F(x, y, z)...Ch. 16.5 - Prove the identity, assuming that the appropriate...Ch. 16.5 - Prob. 24ECh. 16.5 - Prove the identity, assuming that the appropriate...Ch. 16.5 - Prove the identity, assuming that the appropriate...Ch. 16.5 - Prove the identity, assuming that the appropriate...Ch. 16.5 - Prove the identity, assuming that the appropriate...Ch. 16.5 - Prove the identity, assuming that the appropriate...Ch. 16.5 - Let r = x i + y j + z k and r = |r|. 30. Verify...Ch. 16.5 - Prob. 31ECh. 16.5 - Let r = x i + y j + z k and r = |r|. 32. If F =...Ch. 16.5 - Use Greens Theorem in the form of Equation 13 to...Ch. 16.5 - Prob. 34ECh. 16.5 - Prob. 35ECh. 16.5 - Prob. 36ECh. 16.5 - Prob. 37ECh. 16.5 - Maxwells equations relating the electric field E...Ch. 16.5 - Prob. 39ECh. 16.6 - Determine whether the points P and Q lie on the...Ch. 16.6 - Determine whether the points P and Q lie on the...Ch. 16.6 - Identify the surface with the given vector...Ch. 16.6 - Prob. 4ECh. 16.6 - Prob. 5ECh. 16.6 - Prob. 6ECh. 16.6 - Match the equations with the graphs labeled IVI...Ch. 16.6 - Match the equations with the graphs labeled IVI...Ch. 16.6 - Match the equations with the graphs labeled IVI...Ch. 16.6 - Match the equations with the graphs labeled IVI...Ch. 16.6 - Prob. 17ECh. 16.6 - Match the equations with the graphs labeled IVI...Ch. 16.6 - Find a parametric representation for the surface....Ch. 16.6 - Prob. 20ECh. 16.6 - Find a parametric representation for the surface....Ch. 16.6 - Find a parametric representation for the surface....Ch. 16.6 - Find a parametric representation for the surface....Ch. 16.6 - Find a parametric representation for the surface....Ch. 16.6 - Find a parametric representation for the surface....Ch. 16.6 - Find a parametric representation for the surface....Ch. 16.6 - Prob. 29ECh. 16.6 - Find parametric equations for the surface obtained...Ch. 16.6 - Find an equation of the tangent plane to the given...Ch. 16.6 - Find an equation of the tangent plane to the given...Ch. 16.6 - Find an equation of the tangent plane to the given...Ch. 16.6 - Find an equation of the tangent plane to the given...Ch. 16.6 - Prob. 37ECh. 16.6 - Find an equation of the tangent plane to the given...Ch. 16.6 - Find the area of the surface. 39. The part of the...Ch. 16.6 - Prob. 40ECh. 16.6 - Find the area of the surface. 41. The part of the...Ch. 16.6 - Find the area of the surface. 42. The part of the...Ch. 16.6 - Find the area of the surface. 43. The surface z =...Ch. 16.6 - Find the area of the surface. 44. The part of the...Ch. 16.6 - Find the area of the surface. 45. The part of the...Ch. 16.6 - Prob. 46ECh. 16.6 - Find the area of the surface. 47. The part of the...Ch. 16.6 - Find the area of the surface. 48. The helicoid (or...Ch. 16.6 - Find the area of the surface. 49. The surface with...Ch. 16.6 - Find the area of the surface. 50. The part of the...Ch. 16.6 - Prob. 51ECh. 16.6 - Find the area of the surface correct to four...Ch. 16.6 - Find the area of the surface correct to four...Ch. 16.6 - Prob. 54ECh. 16.6 - Find the area of the surface with vector equation...Ch. 16.6 - Prob. 59ECh. 16.6 - (a) Show that the parametric equationsx = acosh u...Ch. 16.6 - Find the area of the part of the spherex2+y2+ z2=...Ch. 16.6 - The figure shows the surface created when the...Ch. 16.6 - Find the area of the part of the spherex2+y2+ z2 =...Ch. 16.7 - LetSbe the surface of the box enclosed by the...Ch. 16.7 - A surface S consists of the cylinderx2+ y2=1, 1 z...Ch. 16.7 - Prob. 3ECh. 16.7 - Suppose thatf(x, y,z)=g(), where g is a function...Ch. 16.7 - Evaluate the surface integral. 5. s (x + y + z)...Ch. 16.7 - Evaluate the surface integral. 6. s xyz dS, Sis...Ch. 16.7 - Evaluate the surface integral. 7. s y dS,Sis the...Ch. 16.7 - Evaluate the surface integral. 8.s (x2+ y2)dS, Sis...Ch. 16.7 - Evaluate the surface integral. 9. s x2yz dS, Sis...Ch. 16.7 - Evaluate the surface integral. 10. s xz dS, S is...Ch. 16.7 - Evaluate the surface integral. 11. s x dS, S is...Ch. 16.7 - Evaluate the surface integral. 12. s y dS, S is...Ch. 16.7 - Evaluate the surface integral. 13. s z2dS, S is...Ch. 16.7 - Evaluate the surface integral. 14. s y2z2 dS, S is...Ch. 16.7 - Prob. 15ECh. 16.7 - Evaluate the surface integral. 16 s y2 dS, S is...Ch. 16.7 - Evaluate the surface integral. 17. s (x2z +...Ch. 16.7 - Evaluate the surface integral. 18. s (x + y + z)...Ch. 16.7 - Evaluate the surface integral. 19. s xz dS, S is...Ch. 16.7 - Evaluate the surface integral. 20. s (x2 + y2 +...Ch. 16.7 - Evaluate the surface integral s F dS for the...Ch. 16.7 - Evaluate the surface integral s F dS for the...Ch. 16.7 - Evaluate the surface integral s F dS for the...Ch. 16.7 - Evaluate the surface integral s F dS for the...Ch. 16.7 - Evaluate the surface integral s F dS for the...Ch. 16.7 - Evaluate the surface integral s F dS for the...Ch. 16.7 - Evaluate the surface integral s F dS for the...Ch. 16.7 - Find a formula for s F dS similar to Formula 10...Ch. 16.7 - Find a formula for s F dS similar to Formula 10...Ch. 16.7 - Find the center of mass of the hemisphere x2 + y2...Ch. 16.7 - Find the mass of a thin funnel in the shape of a...Ch. 16.7 - (a) Give an integral expression for the moment of...Ch. 16.7 - Let S be the part of the sphere x2 + y2 + z2 = 25...Ch. 16.7 - Prob. 43ECh. 16.7 - Prob. 44ECh. 16.7 - Use Gausss Law to find the charge contained in the...Ch. 16.7 - Use Gausss Law to find the charge enclosed by the...Ch. 16.7 - The temperature at the point (x, y, z) in a...Ch. 16.7 - Prob. 48ECh. 16.7 - Let F be an inverse square field, that is, |F(r) =...Ch. 16.8 - 1. A hemisphere H and a portion P of a paraboloid...Ch. 16.8 - Use Stokes Theorem to evaluate s curl F dS. 2....Ch. 16.8 - Use Stokes Theorem to evaluate s curl F dS. 3....Ch. 16.8 - Use Stokes Theorem to evaluate s curl F dS. 4....Ch. 16.8 - F(x, y, z) = xyz i + xy j + x2yz k. S consists of...Ch. 16.8 - Use Stokes Theorem to evaluate s curl F dS. 6....Ch. 16.8 - Use Stokes Theorem to evaluate c F dr. In each...Ch. 16.8 - Use Stokes Theorem to evaluate c F dr. In each...Ch. 16.8 - Use Stokes Theorem to evaluate c F dr. In each...Ch. 16.8 - Use Stokes Theorem to evaluate c F dr. In each...Ch. 16.8 - (a) Use Stokes Theorem to evaluate c F dr, where...Ch. 16.8 - (a) Use Stokes Theorem to evaluate c F dr, where...Ch. 16.8 - Verify that Stokes Theorem is true for the given...Ch. 16.8 - Verify that Stokes Theorem is true for the given...Ch. 16.8 - Verify that Stokes Theorem is true for the given...Ch. 16.8 - A particle moves along line segments from the...Ch. 16.8 - Evaluate c (y + sin x) dx + (z2 + cos y) dy + x3...Ch. 16.8 - If S is a sphere and F satisfies the hypotheses of...Ch. 16.8 - Suppose S and C satisfy the hypotheses of Stokes...Ch. 16.9 - Verify that the Divergence Theorem is true for the...Ch. 16.9 - Verify that the Divergence Theorem is true for the...Ch. 16.9 - Verify that the Divergence Theorem is true for the...Ch. 16.9 - Verify that the Divergence Theorem is true for the...Ch. 16.9 - Use the Divergence Theorem to calculate the...Ch. 16.9 - Use the Divergence Theorem to calculate the...Ch. 16.9 - Use the Divergence Theorem to calculate the...Ch. 16.9 - Use the Divergence Theorem to calculate the...Ch. 16.9 - Use the Divergence Theorem to calculate the...Ch. 16.9 - Use the Divergence Theorem to calculate the...Ch. 16.9 - Use the Divergence Theorem to calculate the...Ch. 16.9 - Use the Divergence Theorem to calculate the...Ch. 16.9 - Use the Divergence Theorem to calculate the...Ch. 16.9 - Prob. 14ECh. 16.9 - Use the Divergence Theorem to evaluate s F dS,...Ch. 16.9 - Let F(x, y, z) = z tan-1(y2) i + z3 ln(x2 + 1) j +...Ch. 16.9 - A vector field F is shown. Use the interpretation...Ch. 16.9 - (a) Are the points P1 and P2 sources or sinks for...Ch. 16.9 - Verify that div E = 0 for the electric field...Ch. 16.9 - Prob. 24ECh. 16.9 - Prove each identity, assuming that S and E satisfy...Ch. 16.9 - Prob. 26ECh. 16.9 - Prob. 27ECh. 16.9 - Prove each identity, assuming that S and E satisfy...Ch. 16.9 - Prob. 29ECh. 16.9 - Prove each identity, assuming that S and E satisfy...Ch. 16.9 - Prob. 31ECh. 16.9 - Prob. 32ECh. 16 - What is a vector field? Give three examples that...Ch. 16 - Prob. 2RCCCh. 16 - Prob. 3RCCCh. 16 - (a) Define the line integral of a vector field F...Ch. 16 - Prob. 5RCCCh. 16 - Prob. 6RCCCh. 16 - Prob. 7RCCCh. 16 - Write expressions for the area enclosed by a curve...Ch. 16 - Prob. 9RCCCh. 16 - Prob. 10RCCCh. 16 - Prob. 11RCCCh. 16 - Prob. 12RCCCh. 16 - Prob. 13RCCCh. 16 - Prob. 14RCCCh. 16 - Prob. 15RCCCh. 16 - Prob. 16RCCCh. 16 - Determine whether the statement is true or false....Ch. 16 - Prob. 2RQCh. 16 - Prob. 3RQCh. 16 - Prob. 4RQCh. 16 - Prob. 5RQCh. 16 - Prob. 6RQCh. 16 - Determine whether the statement is true or false....Ch. 16 - Prob. 8RQCh. 16 - Determine whether the statement is true or false....Ch. 16 - Prob. 10RQCh. 16 - Prob. 11RQCh. 16 - Prob. 12RQCh. 16 - Determine whether the statement is true or false....Ch. 16 - A vector field F, a curve C, and a point P are...Ch. 16 - Evaluate the line integral. 2. C x ds, C is the...Ch. 16 - Evaluate the line integral. 3. C yz cos x ds, C: x...Ch. 16 - Evaluate the line integral. 4. C y dx + (x + y2)...Ch. 16 - Evaluate the line integral. 5. C y3 dx + x2 dy, C...Ch. 16 - Evaluate the line integral. 6. C xy dx + ey dy +...Ch. 16 - Evaluate the line integral. 7. C xy dx + y2 dy +...Ch. 16 - Evaluate the line integral. 8. C F dr, where F(x,...Ch. 16 - Evaluate the line integral. 9. C F dr, where...Ch. 16 - Find the work done by the force field F(x, y, z) =...Ch. 16 - Show that F is a conservative vector field. Then...Ch. 16 - Show that F is a conservative vector field. Then...Ch. 16 - Show that F is a conservative and use this fact to...Ch. 16 - Show that F is a conservative and use this fact to...Ch. 16 - Verify that Greens Theorem is true for the line...Ch. 16 - Use Greens Theorem to evaluate C 1+x3dx + 2xydy...Ch. 16 - Prob. 17RECh. 16 - Find curl F and div F if F(x, y, z) = e-x sin y i...Ch. 16 - Show that there is no vector field G such that...Ch. 16 - If F and G are vector fields whose component...Ch. 16 - If C is any piecewise-smooth simple closed plane...Ch. 16 - If f and g are twice differentiable functions,...Ch. 16 - If f is a harmonic function, that is, 2f = 0, show...Ch. 16 - Prob. 24RECh. 16 - Find the area of the part of the surface z = x2 +...Ch. 16 - Evaluate the surface integral. 27. S z dS, where S...Ch. 16 - Evaluate the surface integral. 28. s (x2z +...Ch. 16 - Evaluate the surface integral. 29. S F dS, where...Ch. 16 - Evaluate the surface integral. 30. S F dS, where...Ch. 16 - Verify that Stokes Theorem is true for the vector...Ch. 16 - Use Stokes Theorem to evaluate s curl F dS, where...Ch. 16 - Use Stokes Theorem to evaluate C F dr, where F(x,...Ch. 16 - Use the Divergence Theorem to calculate the...Ch. 16 - Verify that the Divergence Theorem is true for the...Ch. 16 - Compute the outward flux of F(x, y, z) =...Ch. 16 - Let F(x, y, z) = (3x2 yz 3y) i + (x3z 3x) j +...Ch. 16 - Prob. 38RECh. 16 - Prob. 39RECh. 16 - If the components of F have continuous second...Ch. 16 - Prob. 41RECh. 16 - 1. Let S be a smooth parametric surface and let P...Ch. 16 - Find the positively oriented simple closed curve C...Ch. 16 - Let C be a simple closed piecewise-smooth space...Ch. 16 - Prove the following identity: (F G) = (F )G + (G...Ch. 16 - Prob. 6P
Knowledge Booster
Learn more about
Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, calculus and related others by exploring similar questions and additional content below.Similar questions
Recommended textbooks for you
- Algebra & Trigonometry with Analytic GeometryAlgebraISBN:9781133382119Author:SwokowskiPublisher:Cengage
 Elementary Geometry For College Students, 7eGeometryISBN:9781337614085Author:Alexander, Daniel C.; Koeberlein, Geralyn M.Publisher:Cengage,
Elementary Geometry For College Students, 7eGeometryISBN:9781337614085Author:Alexander, Daniel C.; Koeberlein, Geralyn M.Publisher:Cengage, Mathematics For Machine TechnologyAdvanced MathISBN:9781337798310Author:Peterson, John.Publisher:Cengage Learning,
Mathematics For Machine TechnologyAdvanced MathISBN:9781337798310Author:Peterson, John.Publisher:Cengage Learning,  Trigonometry (MindTap Course List)TrigonometryISBN:9781337278461Author:Ron LarsonPublisher:Cengage Learning
Trigonometry (MindTap Course List)TrigonometryISBN:9781337278461Author:Ron LarsonPublisher:Cengage Learning

Algebra & Trigonometry with Analytic Geometry
Algebra
ISBN:9781133382119
Author:Swokowski
Publisher:Cengage

Elementary Geometry For College Students, 7e
Geometry
ISBN:9781337614085
Author:Alexander, Daniel C.; Koeberlein, Geralyn M.
Publisher:Cengage,

Mathematics For Machine Technology
Advanced Math
ISBN:9781337798310
Author:Peterson, John.
Publisher:Cengage Learning,

Trigonometry (MindTap Course List)
Trigonometry
ISBN:9781337278461
Author:Ron Larson
Publisher:Cengage Learning
Introduction to Triple Integrals; Author: Mathispower4u;https://www.youtube.com/watch?v=CPR0ZD0IYVE;License: Standard YouTube License, CC-BY