
Calculus: Early Transcendentals
8th Edition
ISBN: 9781285741550
Author: James Stewart
Publisher: Cengage Learning
expand_more
expand_more
format_list_bulleted
Concept explainers
Textbook Question
Chapter 16.7, Problem 4E
Suppose that f(x, y, z) = g(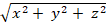 ), where g is a function of one variable such that g(2) = −5. Evaluate ∬S f(x, y, z) dS, where S is the sphere x2 + y2 + z2 = 4.
), where g is a function of one variable such that g(2) = −5. Evaluate ∬S f(x, y, z) dS, where S is the sphere x2 + y2 + z2 = 4.
Expert Solution & Answer
Want to see the full answer?
Check out a sample textbook solution
Students have asked these similar questions
Find the maximum value of f(x, y, z) = 4x + 2y − 8z on the sphere x2 + y2 +z2 = 21.
Suppose that the plane tangent to the surface z=f(x, y) at (−1, 4, 5) has equation z+5x+1y=4
Estimate f(−1.1, 4.1)
The minimum value of f(x,y,z) = x^2 -2y + 2z^2 on the sphere x^2 + y^2 + z^2 =1 is ....?
Chapter 16 Solutions
Calculus: Early Transcendentals
Ch. 16.1 - Sketch the vector field F by drawing a diagram...Ch. 16.1 - Sketch the vector field F by drawing a diagram...Ch. 16.1 - Sketch the vector field F by drawing a diagram...Ch. 16.1 - Sketch the vector field F by drawing a diagram...Ch. 16.1 - Sketch the vector field F by drawing a diagram...Ch. 16.1 - Sketch the vector field F by drawing a diagram...Ch. 16.1 - Sketch the vector field F by drawing a diagram...Ch. 16.1 - Sketch the vector field F by drawing a diagram...Ch. 16.1 - Sketch the vector field F by drawing a diagram...Ch. 16.1 - Sketch the vector field F by drawing a diagram...
Ch. 16.1 - Match the vector fields F with the plots labeled...Ch. 16.1 - Match the vector fields F with the plots labeled...Ch. 16.1 - Match the vector fields F with the plots labeled...Ch. 16.1 - Match the vector fields F with the plots labeled...Ch. 16.1 - Match the vector fields F on 3 with the plots...Ch. 16.1 - Match the vector fields F on 3 with the plots...Ch. 16.1 - Match the vector fields F on 3 with the plots...Ch. 16.1 - Match the vector fields F on 3 with the plots...Ch. 16.1 - Find the gradient vector field of f. 21. f(x, y) =...Ch. 16.1 - Find the gradient vector field of f. 22. f(s, t) =...Ch. 16.1 - Find the gradient vector field of f. 23. f(x, y,...Ch. 16.1 - Find the gradient vector field of f. 24. f(x, y,...Ch. 16.1 - Find the gradient vector field f of f and sketch...Ch. 16.1 - Find the gradient vector field f of f and sketch...Ch. 16.1 - Match the functions f with the plots of their...Ch. 16.1 - Match the functions f with the plots of their...Ch. 16.1 - Match the functions f with the plots of their...Ch. 16.1 - Match the functions f with the plots of their...Ch. 16.1 - A particle moves in a velocity field V(x, y) = x2,...Ch. 16.1 - At time t = 1, a particle is located at position...Ch. 16.1 - The flow lines (or streamlines) of a vector field...Ch. 16.1 - (a) Sketch the vector field F(x, y) = i + x j and...Ch. 16.2 - Evaluate the line integral, where C is the given...Ch. 16.2 - Evaluate the line integral, where C is the given...Ch. 16.2 - Evaluate the line integral, where C is the given...Ch. 16.2 - Evaluate the line integral, where C is the given...Ch. 16.2 - Evaluate the line integral, where C is the given...Ch. 16.2 - Evaluate the line integral, where C is the given...Ch. 16.2 - Evaluate the line integral, where C is the given...Ch. 16.2 - Evaluate the line integral, where C is the given...Ch. 16.2 - Evaluate the line integral, where C is the given...Ch. 16.2 - Evaluate the line integral, where C is the given...Ch. 16.2 - Evaluate the line integral, where C is the given...Ch. 16.2 - Evaluate the line integral, where C is the given...Ch. 16.2 - Evaluate the line integral, where C is the given...Ch. 16.2 - Evaluate the line integral, where C is the given...Ch. 16.2 - Evaluate the line integral, where C is the given...Ch. 16.2 - Evaluate the line integral, where C is the given...Ch. 16.2 - Let F be the vector field shown in the figure. (a)...Ch. 16.2 - The figure shows a vector field F and two curves...Ch. 16.2 - Prob. 19ECh. 16.2 - Prob. 20ECh. 16.2 - Evaluate the line integral C F dr, where C is...Ch. 16.2 - Evaluate the line integral C F dr, where C is...Ch. 16.2 - Use a calculator to evaluate the line integral...Ch. 16.2 - Use a calculator to evaluate the line integral...Ch. 16.2 - Use a calculator to evaluate the line integral...Ch. 16.2 - Use a calculator to evaluate the line integral...Ch. 16.2 - Prob. 31ECh. 16.2 - (a) Find the work done by the force field F(x, y)...Ch. 16.2 - A thin wire is bent into the shape of a semicircle...Ch. 16.2 - A thin wire has the shape of the first-quadrant...Ch. 16.2 - Prob. 35ECh. 16.2 - Prob. 36ECh. 16.2 - If a wire with linear density (x, y) lies along a...Ch. 16.2 - If a wire with linear density (x, y, z) lies along...Ch. 16.2 - Find the work done by the force field F(x, y) = x...Ch. 16.2 - Find the work done by the force field F(x, y) = x2...Ch. 16.2 - Find the work done by the force field F(x, y, z) =...Ch. 16.2 - The force exerted by an electric charge at the...Ch. 16.2 - The position of an object with mass m at time t is...Ch. 16.2 - Prob. 44ECh. 16.2 - A 160-lb man carries a 25-lb can of paint up a...Ch. 16.2 - Prob. 46ECh. 16.2 - (a) Show that a constant force field does zero...Ch. 16.2 - Prob. 48ECh. 16.2 - Prob. 49ECh. 16.2 - Prob. 50ECh. 16.2 - An object moves along the curve C shown in the...Ch. 16.2 - Experiments show that a steady current I in a long...Ch. 16.3 - The figure shows a curve C and a contour map of a...Ch. 16.3 - A table of values of a function f with continuous...Ch. 16.3 - Determine whether or not F is a conservative...Ch. 16.3 - Determine whether or not F is a conservative...Ch. 16.3 - Determine whether or not F is a conservative...Ch. 16.3 - Determine whether or not F is a conservative...Ch. 16.3 - Determine whether or not F is a conservative...Ch. 16.3 - Determine whether or not F is a conservative...Ch. 16.3 - Determine whether or not F is a conservative...Ch. 16.3 - Determine whether or not F is a conservative...Ch. 16.3 - The figure shows the vector field F(x, y) = 2xy,...Ch. 16.3 - Prob. 12ECh. 16.3 - (a) Find a function f such that F = f and (b) use...Ch. 16.3 - (a) Find a function f such that F = f and (b) use...Ch. 16.3 - (a) Find a function f such that F = f and (b) use...Ch. 16.3 - Prob. 16ECh. 16.3 - Prob. 17ECh. 16.3 - (a) Find a function f such that F = f and (b) use...Ch. 16.3 - Show that the line integral is independent of path...Ch. 16.3 - Show that the line integral is independent of path...Ch. 16.3 - Suppose youre asked to determine the curve that...Ch. 16.3 - Suppose an experiment determines that the amount...Ch. 16.3 - Find the work done by the force field F in moving...Ch. 16.3 - Find the work done by the force field F in moving...Ch. 16.3 - Is the vector field shown in the figure...Ch. 16.3 - Is the vector field shown in the figure...Ch. 16.3 - Let F = f, where f(x, y) = sin(x 2y). Find...Ch. 16.3 - Show that if the vector field F = P i + Q j + R k...Ch. 16.3 - Use Exercise 29 to show that the line integral C y...Ch. 16.3 - Determine whether or not the given set is (a)...Ch. 16.3 - Determine whether or not the given set is (a)...Ch. 16.3 - Prob. 33ECh. 16.3 - Determine whether or not the given set is (a)...Ch. 16.3 - Let F(x, y) = yi+xjx2+y2 (a) Show that P/y=Q/x....Ch. 16.4 - Evaluate the line integral by two methods: (a)...Ch. 16.4 - Evaluate the line integral by two methods: (a)...Ch. 16.4 - Evaluate the line integral by two methods: (a)...Ch. 16.4 - Evaluate the line integral by two methods: (a)...Ch. 16.4 - Use Greens Theorem to evaluate the line integral...Ch. 16.4 - Use Greens Theorem to evaluate the line integral...Ch. 16.4 - Use Greens Theorem to evaluate the line integral...Ch. 16.4 - Use Greens Theorem to evaluate the line integral...Ch. 16.4 - Use Greens Theorem to evaluate the line integral...Ch. 16.4 - Use Greens Theorem to evaluate the line integral...Ch. 16.4 - Use Greens Theorem to evaluate C F dr. (Check the...Ch. 16.4 - Use Greens Theorem to evaluate C F dr. (Check the...Ch. 16.4 - Use Greens Theorem to evaluate C F dr. (Check the...Ch. 16.4 - Use Greens Theorem to evaluate C F dr. (Check the...Ch. 16.4 - Prob. 17ECh. 16.4 - A particle starts at the origin, moves along the...Ch. 16.4 - Use one of the formulas in (5) to find the area...Ch. 16.4 - Prob. 20ECh. 16.4 - (a) If C is the line segment connecting the point...Ch. 16.4 - Let D be a region bounded by a simple closed path...Ch. 16.4 - Use Exercise 22 to find the centroid of a...Ch. 16.4 - Use Exercise 22 to find the centroid of the...Ch. 16.4 - A plane lamina with constant density (x, y) = ...Ch. 16.4 - Prob. 26ECh. 16.4 - Use the method of Example 5 to calculate C F dr,...Ch. 16.4 - Calculate C F dr, where F(x, y) = x2 + y, 3x y2...Ch. 16.4 - If F is the vector field of Example 5, show that C...Ch. 16.4 - Complete the proof of the special case of Greens...Ch. 16.4 - Use Greens Theorem to prove the change of...Ch. 16.5 - Find (a) the curl and (b) the divergence of the...Ch. 16.5 - Find (a) the curl and (b) the divergence of the...Ch. 16.5 - Find (a) the curl and (b) the divergence of the...Ch. 16.5 - Find (a) the curl and (b) the divergence of the...Ch. 16.5 - Find (a) the curl and (b) the divergence of the...Ch. 16.5 - Prob. 6ECh. 16.5 - Find (a) the curl and (b) the divergence of the...Ch. 16.5 - Find (a) the curl and (b) the divergence of the...Ch. 16.5 - The vector field F is shown in the xy-plane and...Ch. 16.5 - The vector field F is shown in the xy-plane and...Ch. 16.5 - The vector field F is shown in the xy-plane and...Ch. 16.5 - Let f be a scalar field and F a vector field....Ch. 16.5 - Determine whether or not the vector field is...Ch. 16.5 - Determine whether or not the vector field is...Ch. 16.5 - Determine whether or not the vector field is...Ch. 16.5 - Determine whether or not the vector field is...Ch. 16.5 - Determine whether or not the vector field is...Ch. 16.5 - Determine whether or not the vector field is...Ch. 16.5 - Is there a vector field G on 3 such that curl G =...Ch. 16.5 - Is there a vector field G on 3 such that curl G =...Ch. 16.5 - Show that any vector field of the form F(x, y, z)...Ch. 16.5 - Show that any vector field of the form F(x, y, z)...Ch. 16.5 - Prove the identity, assuming that the appropriate...Ch. 16.5 - Prob. 24ECh. 16.5 - Prove the identity, assuming that the appropriate...Ch. 16.5 - Prove the identity, assuming that the appropriate...Ch. 16.5 - Prove the identity, assuming that the appropriate...Ch. 16.5 - Prove the identity, assuming that the appropriate...Ch. 16.5 - Prove the identity, assuming that the appropriate...Ch. 16.5 - Let r = x i + y j + z k and r = |r|. 30. Verify...Ch. 16.5 - Prob. 31ECh. 16.5 - Let r = x i + y j + z k and r = |r|. 32. If F =...Ch. 16.5 - Use Greens Theorem in the form of Equation 13 to...Ch. 16.5 - Prob. 34ECh. 16.5 - Prob. 35ECh. 16.5 - Prob. 36ECh. 16.5 - Prob. 37ECh. 16.5 - Maxwells equations relating the electric field E...Ch. 16.5 - Prob. 39ECh. 16.6 - Determine whether the points P and Q lie on the...Ch. 16.6 - Determine whether the points P and Q lie on the...Ch. 16.6 - Identify the surface with the given vector...Ch. 16.6 - Prob. 4ECh. 16.6 - Prob. 5ECh. 16.6 - Prob. 6ECh. 16.6 - Match the equations with the graphs labeled IVI...Ch. 16.6 - Match the equations with the graphs labeled IVI...Ch. 16.6 - Match the equations with the graphs labeled IVI...Ch. 16.6 - Match the equations with the graphs labeled IVI...Ch. 16.6 - Prob. 17ECh. 16.6 - Match the equations with the graphs labeled IVI...Ch. 16.6 - Find a parametric representation for the surface....Ch. 16.6 - Prob. 20ECh. 16.6 - Find a parametric representation for the surface....Ch. 16.6 - Find a parametric representation for the surface....Ch. 16.6 - Find a parametric representation for the surface....Ch. 16.6 - Find a parametric representation for the surface....Ch. 16.6 - Find a parametric representation for the surface....Ch. 16.6 - Find a parametric representation for the surface....Ch. 16.6 - Prob. 29ECh. 16.6 - Find parametric equations for the surface obtained...Ch. 16.6 - Find an equation of the tangent plane to the given...Ch. 16.6 - Find an equation of the tangent plane to the given...Ch. 16.6 - Find an equation of the tangent plane to the given...Ch. 16.6 - Find an equation of the tangent plane to the given...Ch. 16.6 - Prob. 37ECh. 16.6 - Find an equation of the tangent plane to the given...Ch. 16.6 - Find the area of the surface. 39. The part of the...Ch. 16.6 - Prob. 40ECh. 16.6 - Find the area of the surface. 41. The part of the...Ch. 16.6 - Find the area of the surface. 42. The part of the...Ch. 16.6 - Find the area of the surface. 43. The surface z =...Ch. 16.6 - Find the area of the surface. 44. The part of the...Ch. 16.6 - Find the area of the surface. 45. The part of the...Ch. 16.6 - Prob. 46ECh. 16.6 - Find the area of the surface. 47. The part of the...Ch. 16.6 - Find the area of the surface. 48. The helicoid (or...Ch. 16.6 - Find the area of the surface. 49. The surface with...Ch. 16.6 - Find the area of the surface. 50. The part of the...Ch. 16.6 - Prob. 51ECh. 16.6 - Find the area of the surface correct to four...Ch. 16.6 - Find the area of the surface correct to four...Ch. 16.6 - Prob. 54ECh. 16.6 - Find the area of the surface with vector equation...Ch. 16.6 - Prob. 59ECh. 16.6 - (a) Show that the parametric equationsx = acosh u...Ch. 16.6 - Find the area of the part of the spherex2+y2+ z2=...Ch. 16.6 - The figure shows the surface created when the...Ch. 16.6 - Find the area of the part of the spherex2+y2+ z2 =...Ch. 16.7 - LetSbe the surface of the box enclosed by the...Ch. 16.7 - A surface S consists of the cylinderx2+ y2=1, 1 z...Ch. 16.7 - Prob. 3ECh. 16.7 - Suppose thatf(x, y,z)=g(), where g is a function...Ch. 16.7 - Evaluate the surface integral. 5. s (x + y + z)...Ch. 16.7 - Evaluate the surface integral. 6. s xyz dS, Sis...Ch. 16.7 - Evaluate the surface integral. 7. s y dS,Sis the...Ch. 16.7 - Evaluate the surface integral. 8.s (x2+ y2)dS, Sis...Ch. 16.7 - Evaluate the surface integral. 9. s x2yz dS, Sis...Ch. 16.7 - Evaluate the surface integral. 10. s xz dS, S is...Ch. 16.7 - Evaluate the surface integral. 11. s x dS, S is...Ch. 16.7 - Evaluate the surface integral. 12. s y dS, S is...Ch. 16.7 - Evaluate the surface integral. 13. s z2dS, S is...Ch. 16.7 - Evaluate the surface integral. 14. s y2z2 dS, S is...Ch. 16.7 - Prob. 15ECh. 16.7 - Evaluate the surface integral. 16 s y2 dS, S is...Ch. 16.7 - Evaluate the surface integral. 17. s (x2z +...Ch. 16.7 - Evaluate the surface integral. 18. s (x + y + z)...Ch. 16.7 - Evaluate the surface integral. 19. s xz dS, S is...Ch. 16.7 - Evaluate the surface integral. 20. s (x2 + y2 +...Ch. 16.7 - Evaluate the surface integral s F dS for the...Ch. 16.7 - Evaluate the surface integral s F dS for the...Ch. 16.7 - Evaluate the surface integral s F dS for the...Ch. 16.7 - Evaluate the surface integral s F dS for the...Ch. 16.7 - Evaluate the surface integral s F dS for the...Ch. 16.7 - Evaluate the surface integral s F dS for the...Ch. 16.7 - Evaluate the surface integral s F dS for the...Ch. 16.7 - Find a formula for s F dS similar to Formula 10...Ch. 16.7 - Find a formula for s F dS similar to Formula 10...Ch. 16.7 - Find the center of mass of the hemisphere x2 + y2...Ch. 16.7 - Find the mass of a thin funnel in the shape of a...Ch. 16.7 - (a) Give an integral expression for the moment of...Ch. 16.7 - Let S be the part of the sphere x2 + y2 + z2 = 25...Ch. 16.7 - Prob. 43ECh. 16.7 - Prob. 44ECh. 16.7 - Use Gausss Law to find the charge contained in the...Ch. 16.7 - Use Gausss Law to find the charge enclosed by the...Ch. 16.7 - The temperature at the point (x, y, z) in a...Ch. 16.7 - Prob. 48ECh. 16.7 - Let F be an inverse square field, that is, |F(r) =...Ch. 16.8 - 1. A hemisphere H and a portion P of a paraboloid...Ch. 16.8 - Use Stokes Theorem to evaluate s curl F dS. 2....Ch. 16.8 - Use Stokes Theorem to evaluate s curl F dS. 3....Ch. 16.8 - Use Stokes Theorem to evaluate s curl F dS. 4....Ch. 16.8 - F(x, y, z) = xyz i + xy j + x2yz k. S consists of...Ch. 16.8 - Use Stokes Theorem to evaluate s curl F dS. 6....Ch. 16.8 - Use Stokes Theorem to evaluate c F dr. In each...Ch. 16.8 - Use Stokes Theorem to evaluate c F dr. In each...Ch. 16.8 - Use Stokes Theorem to evaluate c F dr. In each...Ch. 16.8 - Use Stokes Theorem to evaluate c F dr. In each...Ch. 16.8 - (a) Use Stokes Theorem to evaluate c F dr, where...Ch. 16.8 - (a) Use Stokes Theorem to evaluate c F dr, where...Ch. 16.8 - Verify that Stokes Theorem is true for the given...Ch. 16.8 - Verify that Stokes Theorem is true for the given...Ch. 16.8 - Verify that Stokes Theorem is true for the given...Ch. 16.8 - A particle moves along line segments from the...Ch. 16.8 - Evaluate c (y + sin x) dx + (z2 + cos y) dy + x3...Ch. 16.8 - If S is a sphere and F satisfies the hypotheses of...Ch. 16.8 - Suppose S and C satisfy the hypotheses of Stokes...Ch. 16.9 - Verify that the Divergence Theorem is true for the...Ch. 16.9 - Verify that the Divergence Theorem is true for the...Ch. 16.9 - Verify that the Divergence Theorem is true for the...Ch. 16.9 - Verify that the Divergence Theorem is true for the...Ch. 16.9 - Use the Divergence Theorem to calculate the...Ch. 16.9 - Use the Divergence Theorem to calculate the...Ch. 16.9 - Use the Divergence Theorem to calculate the...Ch. 16.9 - Use the Divergence Theorem to calculate the...Ch. 16.9 - Use the Divergence Theorem to calculate the...Ch. 16.9 - Use the Divergence Theorem to calculate the...Ch. 16.9 - Use the Divergence Theorem to calculate the...Ch. 16.9 - Use the Divergence Theorem to calculate the...Ch. 16.9 - Use the Divergence Theorem to calculate the...Ch. 16.9 - Prob. 14ECh. 16.9 - Use the Divergence Theorem to evaluate s F dS,...Ch. 16.9 - Let F(x, y, z) = z tan-1(y2) i + z3 ln(x2 + 1) j +...Ch. 16.9 - A vector field F is shown. Use the interpretation...Ch. 16.9 - (a) Are the points P1 and P2 sources or sinks for...Ch. 16.9 - Verify that div E = 0 for the electric field...Ch. 16.9 - Prob. 24ECh. 16.9 - Prove each identity, assuming that S and E satisfy...Ch. 16.9 - Prob. 26ECh. 16.9 - Prob. 27ECh. 16.9 - Prove each identity, assuming that S and E satisfy...Ch. 16.9 - Prob. 29ECh. 16.9 - Prove each identity, assuming that S and E satisfy...Ch. 16.9 - Prob. 31ECh. 16.9 - Prob. 32ECh. 16 - What is a vector field? Give three examples that...Ch. 16 - Prob. 2RCCCh. 16 - Prob. 3RCCCh. 16 - (a) Define the line integral of a vector field F...Ch. 16 - Prob. 5RCCCh. 16 - Prob. 6RCCCh. 16 - Prob. 7RCCCh. 16 - Write expressions for the area enclosed by a curve...Ch. 16 - Prob. 9RCCCh. 16 - Prob. 10RCCCh. 16 - Prob. 11RCCCh. 16 - Prob. 12RCCCh. 16 - Prob. 13RCCCh. 16 - Prob. 14RCCCh. 16 - Prob. 15RCCCh. 16 - Prob. 16RCCCh. 16 - Determine whether the statement is true or false....Ch. 16 - Prob. 2RQCh. 16 - Prob. 3RQCh. 16 - Prob. 4RQCh. 16 - Prob. 5RQCh. 16 - Prob. 6RQCh. 16 - Determine whether the statement is true or false....Ch. 16 - Prob. 8RQCh. 16 - Determine whether the statement is true or false....Ch. 16 - Prob. 10RQCh. 16 - Prob. 11RQCh. 16 - Prob. 12RQCh. 16 - Determine whether the statement is true or false....Ch. 16 - A vector field F, a curve C, and a point P are...Ch. 16 - Evaluate the line integral. 2. C x ds, C is the...Ch. 16 - Evaluate the line integral. 3. C yz cos x ds, C: x...Ch. 16 - Evaluate the line integral. 4. C y dx + (x + y2)...Ch. 16 - Evaluate the line integral. 5. C y3 dx + x2 dy, C...Ch. 16 - Evaluate the line integral. 6. C xy dx + ey dy +...Ch. 16 - Evaluate the line integral. 7. C xy dx + y2 dy +...Ch. 16 - Evaluate the line integral. 8. C F dr, where F(x,...Ch. 16 - Evaluate the line integral. 9. C F dr, where...Ch. 16 - Find the work done by the force field F(x, y, z) =...Ch. 16 - Show that F is a conservative vector field. Then...Ch. 16 - Show that F is a conservative vector field. Then...Ch. 16 - Show that F is a conservative and use this fact to...Ch. 16 - Show that F is a conservative and use this fact to...Ch. 16 - Verify that Greens Theorem is true for the line...Ch. 16 - Use Greens Theorem to evaluate C 1+x3dx + 2xydy...Ch. 16 - Prob. 17RECh. 16 - Find curl F and div F if F(x, y, z) = e-x sin y i...Ch. 16 - Show that there is no vector field G such that...Ch. 16 - If F and G are vector fields whose component...Ch. 16 - If C is any piecewise-smooth simple closed plane...Ch. 16 - If f and g are twice differentiable functions,...Ch. 16 - If f is a harmonic function, that is, 2f = 0, show...Ch. 16 - Prob. 24RECh. 16 - Find the area of the part of the surface z = x2 +...Ch. 16 - Evaluate the surface integral. 27. S z dS, where S...Ch. 16 - Evaluate the surface integral. 28. s (x2z +...Ch. 16 - Evaluate the surface integral. 29. S F dS, where...Ch. 16 - Evaluate the surface integral. 30. S F dS, where...Ch. 16 - Verify that Stokes Theorem is true for the vector...Ch. 16 - Use Stokes Theorem to evaluate s curl F dS, where...Ch. 16 - Use Stokes Theorem to evaluate C F dr, where F(x,...Ch. 16 - Use the Divergence Theorem to calculate the...Ch. 16 - Verify that the Divergence Theorem is true for the...Ch. 16 - Compute the outward flux of F(x, y, z) =...Ch. 16 - Let F(x, y, z) = (3x2 yz 3y) i + (x3z 3x) j +...Ch. 16 - Prob. 38RECh. 16 - Prob. 39RECh. 16 - If the components of F have continuous second...Ch. 16 - Prob. 41RECh. 16 - 1. Let S be a smooth parametric surface and let P...Ch. 16 - Find the positively oriented simple closed curve C...Ch. 16 - Let C be a simple closed piecewise-smooth space...Ch. 16 - Prove the following identity: (F G) = (F )G + (G...Ch. 16 - Prob. 6P
Knowledge Booster
Learn more about
Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, calculus and related others by exploring similar questions and additional content below.Similar questions
- If x and y are elements of an ordered integral domain D, prove the following inequalities. a. x22xy+y20 b. x2+y2xy c. x2+y2xyarrow_forwardDoes there exist a surface x(u, v) such that E=G=1,F=0 and L=1,M=−1,N=0?arrow_forwardSuppose that the Celsius temperature at the point (x, y, z) on the sphere x2 + y2 + z2 = 1 is T = 400xyz2. Locate the highest and lowest temperatures on the sphere.arrow_forward
Recommended textbooks for you
 Elementary Geometry For College Students, 7eGeometryISBN:9781337614085Author:Alexander, Daniel C.; Koeberlein, Geralyn M.Publisher:Cengage,
Elementary Geometry For College Students, 7eGeometryISBN:9781337614085Author:Alexander, Daniel C.; Koeberlein, Geralyn M.Publisher:Cengage, Elements Of Modern AlgebraAlgebraISBN:9781285463230Author:Gilbert, Linda, JimmiePublisher:Cengage Learning,
Elements Of Modern AlgebraAlgebraISBN:9781285463230Author:Gilbert, Linda, JimmiePublisher:Cengage Learning,

Elementary Geometry For College Students, 7e
Geometry
ISBN:9781337614085
Author:Alexander, Daniel C.; Koeberlein, Geralyn M.
Publisher:Cengage,

Elements Of Modern Algebra
Algebra
ISBN:9781285463230
Author:Gilbert, Linda, Jimmie
Publisher:Cengage Learning,
What is a Function? Business Mathematics and Statistics; Author: Edmerls;https://www.youtube.com/watch?v=fcGNFyqRzuI;License: Standard YouTube License, CC-BY
FUNCTIONS CONCEPTS FOR CBSE/ISC/JEE/NDA/CET/BANKING/GRE/MBA/COMEDK; Author: Neha Agrawal Mathematically Inclined;https://www.youtube.com/watch?v=hhbYynJwBqk;License: Standard YouTube License, CC-BY