
Chemistry
10th Edition
ISBN: 9781305957404
Author: Steven S. Zumdahl, Susan A. Zumdahl, Donald J. DeCoste
Publisher: Cengage Learning
expand_more
expand_more
format_list_bulleted
Concept explainers
Textbook Question
Chapter 3, Problem 7RQ
Consider the hypothetical reaction between A2 and AB pictured below.
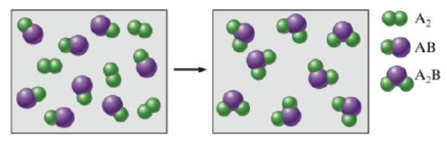
What is the balanced equation? lf 2.50 moles of A2 are reacted with excess AB, what amount (moles) of product will form? If the mass of AB is 30.0 u and the mass of A2 are 40.0 u, what is the mass of the product? If 15.0 g of AB is reacted, what mass of A2 is required to react with all of the AB, and what mass of product is formed?
Expert Solution & Answer
Trending nowThis is a popular solution!

Chapter 3 Solutions
Chemistry
Ch. 3 - Prob. 1RQCh. 3 - Atomic masses are relative masses. What does this...Ch. 3 - The atomic mass of boron (B) is given in the...Ch. 3 - What three conversion factors and in what order...Ch. 3 - Fig. 5-5 illustrates a schematic diagram of a...Ch. 3 - What is the difference between the empirical and...Ch. 3 - Consider the hypothetical reaction between A2 and...Ch. 3 - Prob. 8RQCh. 3 - Consider the following mixture of SO2(g) and...Ch. 3 - Why is the actual yield of a reaction often less...
Ch. 3 - The following are actual student responses to the...Ch. 3 - What information do we get from a chemical...Ch. 3 - True or false? The atom with the largest subscript...Ch. 3 - You have a 20.0-g sample of silver metal. You are...Ch. 3 - You are making cookies and are missing a key...Ch. 3 - Nitrogen gas (N2) and hydrogen gas (H2) react to...Ch. 3 - For the preceding question, which of the following...Ch. 3 - You know that chemical A reacts with chemical B....Ch. 3 - Prob. 9ALQCh. 3 - Consider an iron bar on a balance as shown. As the...Ch. 3 - You may have noticed that water sometimes drips...Ch. 3 - Prob. 12ALQCh. 3 - What is true about the chemical properties of the...Ch. 3 - Is there a difference between a homogeneous...Ch. 3 - Chlorine exists mainly as two isotopes, 37Cl and...Ch. 3 - The average mass of a carbon atom is 12.011....Ch. 3 - Can the subscripts in a chemical formula be...Ch. 3 - Consider the equation 2A + B . A2B. If you mix 1.0...Ch. 3 - According to the law of conservation of mass, mass...Ch. 3 - Which of the following pairs of compounds have the...Ch. 3 - Atoms of three different elements are represented...Ch. 3 - In chemistry, what is meant by the term mole? What...Ch. 3 - Which (if any) of the following is (are) true...Ch. 3 - Consider the equation 3A + B C + D. You react 4...Ch. 3 - The atomic masses in die periodic table are...Ch. 3 - Avogadros number, molar mass, and the chemical...Ch. 3 - If you had a mole of U.S. dollar bills and equally...Ch. 3 - Prob. 28QCh. 3 - Which of the following compounds have the same...Ch. 3 - What is the difference between the molar mass and...Ch. 3 - How is the mass percent of elements in a compound...Ch. 3 - A balanced chemical equation contains a large...Ch. 3 - Prob. 33QCh. 3 - Hydrogen gas and oxygen gas react to form water,...Ch. 3 - What is the theoretical yield for a reaction, and...Ch. 3 - What does it mean to say a reactant is present in...Ch. 3 - Consider the following generic reaction: A2B2 + 2C...Ch. 3 - Consider the following generic reaction:...Ch. 3 - An element consists of 1.40% of an isotope with...Ch. 3 - An element X bas five major isotopes, which are...Ch. 3 - The element rhenium (Re) bas two naturally...Ch. 3 - Assume silicon has three major isotopes in nature...Ch. 3 - The element europium exists in nature as two...Ch. 3 - The element silver (Ag) has two naturally...Ch. 3 - The mass spectrum of bromine (Br2) consists of...Ch. 3 - The stable isotopes of iron arc 54Fe, 56Fe, 57Fe,...Ch. 3 - Calculate the mass of 500. atoms of iron (Fe).Ch. 3 - What number of Fe atoms and what amount (moles) of...Ch. 3 - Diamond is a natural form of pure carbon. What...Ch. 3 - Chromium (Cr) is a metal that is added to steel to...Ch. 3 - Selective serotonin reuptake inhibitors (SSRIs)...Ch. 3 - The Freons are a class of compounds containing...Ch. 3 - Calculate the molar mass of the following...Ch. 3 - Calculate the molar mass of the following...Ch. 3 - What amount (moles) of compound is present in 1.00...Ch. 3 - What amount (moles) of compound is present in 1.00...Ch. 3 - What mass of compound is present in 5.00 moles of...Ch. 3 - What mass of compound is present in 5.00 moles of...Ch. 3 - Prob. 59ECh. 3 - Prob. 60ECh. 3 - What number of molecules (or formula units) are...Ch. 3 - What number of molecules (or formula units) are...Ch. 3 - What number of atoms of nitrogen are present in...Ch. 3 - Prob. 64ECh. 3 - Freon- 12 (CCI2F2) is used as a refrigerant in air...Ch. 3 - Prevacid is used to treat gastroesophageal reflux...Ch. 3 - What amount (moles) is represented by each of...Ch. 3 - What number of atoms of nitrogen are present in...Ch. 3 - Complete the following table.Ch. 3 - Ascorbic acid, or vitamin C (C6H8O6), is an...Ch. 3 - The molecular formula of acetylsalicylic acid...Ch. 3 - Chloral hydrate (C2H3Cl3O2) is a drug formerly...Ch. 3 - Dimethylnitrosamine, (CH3)2N2O , is a carcinogenic...Ch. 3 - Calculate the percent composition by mass of the...Ch. 3 - In 1987 the first substance to act as a...Ch. 3 - The percent by mass of nitrogen for a compound is...Ch. 3 - Arrange the following substances in order of...Ch. 3 - Fungal laccase, a blue protein found in...Ch. 3 - Hemoglobin is the protein that transports oxygen...Ch. 3 - Express the composition of each of the following...Ch. 3 - Considering your answer to Exercise 79, which type...Ch. 3 - Give the empirical formula for each of the...Ch. 3 - Determine the molecular formulas to which the...Ch. 3 - A compound that contains only carbon, hydrogen,...Ch. 3 - The most common form of nylon (nylon-6) is 63.68%...Ch. 3 - There are two binary compounds of mercury and...Ch. 3 - A sample of urea contains 1.121 g N, 0.161 g H,...Ch. 3 - A compound containing only sulfur and nitrogen is...Ch. 3 - Determine the molecular formula of a compound that...Ch. 3 - A compound contains 47.08% carbon, 6.59% hydrogen,...Ch. 3 - Maleic acid is an organic compound composed of...Ch. 3 - One of the components that make up common table...Ch. 3 - A compound contains only C, H, and N. Combustion...Ch. 3 - Cumene is a compound containing only carbon and...Ch. 3 - A compound contains only carbon, hydrogen, and...Ch. 3 - Give the balanced equation for each of the...Ch. 3 - Give the balanced equation for each of the...Ch. 3 - A common demonstration in chemistry courses...Ch. 3 - Iron oxide ores, commonly a mixture of FeO and...Ch. 3 - Balance the following equations: a. Ca(OH)2(aq) +...Ch. 3 - Balance each of the following chemical equations....Ch. 3 - Balance the following equations representing...Ch. 3 - Balance the following equations: a. Cr(s) + S8(s) ...Ch. 3 - Silicon is produced for the chemical and...Ch. 3 - Glass is a mixture of several compounds, but a...Ch. 3 - Phosphorus occurs naturally in the form of...Ch. 3 - The sugar sucrose, which is present in many fruits...Ch. 3 - Over the years, the thermite reaction has been...Ch. 3 - The reaction between potassium chlorate and red...Ch. 3 - The reusable booster rockets of the U.S. space...Ch. 3 - One of relatively few reactions that takes place...Ch. 3 - Prob. 113ECh. 3 - a. Write die balanced equation for the combustion...Ch. 3 - Elixirs such as Atka-Seltzer use the reaction of...Ch. 3 - Aspirin (C9H8O4) is synthesized by reacting...Ch. 3 - Bacterial digestion is an economical method of...Ch. 3 - Phosphorus can be prepared from calcium phosphate...Ch. 3 - Coke is an impure form of carbon that is often...Ch. 3 - The space shuttle environmental control system...Ch. 3 - Consider the reaction between NO(g) and O2(g)...Ch. 3 - Consider the following reaction:...Ch. 3 - Ammonia is produced from the reaction of nitrogen...Ch. 3 - Consider the following unbalanced equation:...Ch. 3 - Hydrogen peroxide is used as a cleansing agent in...Ch. 3 - Silver sulfadiazine bum-treating cream creates a...Ch. 3 - Hydrogen cyanide is produced industrially from the...Ch. 3 - Acrylonitrile C3H3N) is the starting material for...Ch. 3 - Aluminum reacts with bromine, producing aluminum...Ch. 3 - Hexamethylenediamine (C6H16N2) is one of the...Ch. 3 - The reaction of ethane gas (C2H6) with chlorine...Ch. 3 - DDT, an insecticide harmful to fish, birds, and...Ch. 3 - Bornite (Cu3FeS3) is a copper ore used in the...Ch. 3 - Prob. 134ECh. 3 - In using a mass spectrometer, a chemist sees a...Ch. 3 - Boron consists of two isotopes, 10B and 11B....Ch. 3 - A given sample of a xenon fluoride compound...Ch. 3 - Aspartame is an artificial sweetener that is 160...Ch. 3 - Anabolic steroids are performance enhancement...Ch. 3 - In the spring of 1984, concern arose over the...Ch. 3 - You find a compound composed only of element X and...Ch. 3 - What mass of sodium hydroxide has the same number...Ch. 3 - The compound adrenaline contains 56.79% C, 6.56%...Ch. 3 - Adipic acid is an organic compound composed of...Ch. 3 - Vitamin B12, cyanocobalamin, is essential for...Ch. 3 - Some bismuth tablets, a medication used to treat...Ch. 3 - The empirical formula of styrene is CH; the molar...Ch. 3 - Terephthalic acid is an important chemical used in...Ch. 3 - A sample of a hydrocarbon (a compound consisting...Ch. 3 - A binary compound between an unknown element E and...Ch. 3 - A 0.755-g sample of hydrated copper(II) sulfate...Ch. 3 - ABS plastic is a tough, hard plastic used in...Ch. 3 - A sample of LSD (D-lysergic acid diethylamide,...Ch. 3 - Methane (CH4) is the main component of marsh gas....Ch. 3 - A potential fuel for rockets is a combination of...Ch. 3 - A 0.4230-g sample of impure sodium nitrate was...Ch. 3 - Prob. 157AECh. 3 - Commercial brass, an alloy of Zn and Cu, reacts...Ch. 3 - Vitamin A has a molar mass of 286.4 g/mol and a...Ch. 3 - You have seven closed containers, each with equal...Ch. 3 - A substance X2Z has the composition (by mass) of...Ch. 3 - Consider samples of phosphine (PH3), water (H2O),...Ch. 3 - Calculate the number of moles for each compound in...Ch. 3 - Arrange the following substances in order of...Ch. 3 - Para-cresol, a substance used as a disinfectant...Ch. 3 - A compound with molar mass 180.1 g/mol has the...Ch. 3 - Prob. 167CWPCh. 3 - Consider the following unbalanced chemical...Ch. 3 - Sulfur dioxide gas reacts with sodium hydroxide to...Ch. 3 - Gallium arsenide, GaAs, has gained widespread use...Ch. 3 - Consider the following data for three binary...Ch. 3 - Natural rubidium has the average mass of 85.4678 u...Ch. 3 - A compound contains only carbon, hydrogen,...Ch. 3 - Nitric acid is produced commercially by the...Ch. 3 - When the supply of oxygen is limited, iron metal...Ch. 3 - A 9.780-g gaseous mixture contains ethane (C2H6)...Ch. 3 - Zinc and magnesium metal each reacts with...Ch. 3 - A gas contains a mixture of NH3(g) and N2H4(g),...Ch. 3 - Consider a gaseous binary compound with a molar...Ch. 3 - A 2.25-g sample of scandium metal is reacted with...Ch. 3 - Prob. 181CPCh. 3 - The aspirin substitute, acetaminophen (C8H9O2N),...Ch. 3 - An element X forms both a dichloride (XCl2) and a...Ch. 3 - When M2S3(s) is heated in air, it is converted to...Ch. 3 - When aluminum metal is heated with an element from...Ch. 3 - Consider a mixture of potassium chloride and...Ch. 3 - Lanthanum was reacted with hydrogen in a given...Ch. 3 - A 1.500-g sample of a mixture containing only Cu2O...Ch. 3 - Ammonia reacts with O2 to form either NO(g) or...Ch. 3 - You take 1.00 g of an aspirin tablet (a compound...Ch. 3 - With the advent of techniques such as scanning...Ch. 3 - Tetrodotoxin is a toxic chemical found in fugu...Ch. 3 - An iortic compound MX3 is prepared according to...Ch. 3 - The compound As2I4 is synthesized by reaction of...Ch. 3 - A 2.077-g sample of an element, which has an...Ch. 3 - Consider the following balanced chemical equation:...
Knowledge Booster
Learn more about
Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, chemistry and related others by exploring similar questions and additional content below.Similar questions
- When the supply of oxygen is limited, iron metal reacts with oxygen to produce a mixture of FeO and Fe2O3. In a certain experiment, 20.00 g iron metal was reacted with 11.20 g oxygen gas. After the experiment, the iron was totally consumed, and 3.24 g oxygen gas remained. Calculate the amounts of FeO and Fe2O3 formed in this experiment.arrow_forwardThe reaction of iron metal and chlorine gas to give iron(III) chloride is illustrated below. (a) Write the balanced chemical equation for the reaction. (b) Beginning with 10.0 g of iron, what mass of Cl2, in grams, is required for complete reaction? What mass of FeCl3 can be produced? (c) If only 18.5 g of FeCl3 is obtained from 10.0 g of iron and excess Cl2, what is the percent yield? (d) If 10.0 g each of iron and chlorine are combined, what is the theoretical yield of iron(III) chloride?arrow_forwardPotassium superoxide, KO2, is employed in a self-contained breathing apparatus used by emergency personnel as a source of oxygen. The reaction is 4KO2(s)+2H2O(l)4KOH(s)+3O2(g) If a self-contained breathing apparatus is charged with 750 g KO2 and then is used to produce 188 g of oxygen, was all of the KO2 consumed in this reaction? If the KO2 wasnt all consumed, how much is left over and what mass of additional O2 could be produced?arrow_forward
- Over the years, the thermite reaction has been used for welding railroad rails, in incendiary bombs, and to ignite solid fuel rocket motors. The reaction is :math>Fe2O3(s)+2Al(s)2Fe(l)+Al2O3(s) l type='a'> What mass of iron(III) oxide must be used to produce 25.69 g of iron? What mass of aluminum must be used to produce 25.69 g of iron? What is the maximum mass of aluminum oxide that could be produced along with 25.69 g of iron?arrow_forwardThe reaction of methane and water is one way to prepare hydrogen for use as a fuel: CH4(g) + H2O(g) CO(g) + 3 H2(g) If you begin with 995 g of CH4 and 2510 g of water, (a) Which reactant is the limiting reactant? (b) What is the maximum mass of H2 that can be prepared? (c) What mass of the excess reactant remains when the reaction is completed?arrow_forwardHydrogen cyanide is produced industrially from the reaction of gaseous ammonia, oxygen, and methane: 2NH3(g)+3O2(g)+2CH4(g)2HCN(g)+6H2O(g) If 5.00 103 kg each of NH3, O2, and CH4 are reacted, what mass of HCN and of H2O will be produced, assuming 100% yield?arrow_forward
- Copper metal reacts with mine acid. Assume that the reaction is 3Cu(s)+8HNO3(aq)3Cu(NO3)2(aq)+2NO(g)+4H2O(l) If 5.58 g Cu(NO3)2 is eventually obtained, how many grams of nitrogen monoxide, NO, would have formed?arrow_forward4.84 Aluminum chloride (AlCl3) is used as a catalyst in the production of polyisobutylene, which is used in automobile tires. Scrap aluminum metal reacts with chlorine gas (Cl2) to produce AlCl3. Suppose that 2.70 g of Al and 7.10 g of Cl2 are mixed. What is the maximum mass of AlCl3 that could be formed?arrow_forwardThe mass of 2.50 mol of a compound with the formula ECl4, in which E is a nonmetallic element, is 385 g. What is the molar mass of ECl4? What is the identity of E?arrow_forward
- An adult human body contains 6.0 L blood, which contains about 15.5 g hemoglobin per 100.0 mL blood. The molar mass of hemoglobin is approximately 64,500 g/mol and there is 4 mol iron per 1 mol hemoglobin. A news item claims that there is sufficient iron in the hemoglobin of the body that this iron, if it were in the form of metallic iron, could make a 3-in. iron nail that weighs approximately 3.7 g. Show sufficient calculations to either support or refute the claim.arrow_forwardopical hydrocortisone is often used to treat a variety of skin conditions, such as insect bites, eczema, and rashes. Each molecule of hydrocortisone contains 21 atoms of carbon (plus other atoms). The mass percentage of carbon in hydrocortisone is 69.5 8%. What is the molar mass of hydrocortisone?arrow_forward3.117 For the oxides of iron, FeO, Fe2O3, and Fe3O4, describe how you would determine which has the greatest percentage by mass of oxygen. Would you need to look up any information to solve this problem?arrow_forward
arrow_back_ios
arrow_forward_ios
Recommended textbooks for you
 Introductory Chemistry: A FoundationChemistryISBN:9781337399425Author:Steven S. Zumdahl, Donald J. DeCostePublisher:Cengage Learning
Introductory Chemistry: A FoundationChemistryISBN:9781337399425Author:Steven S. Zumdahl, Donald J. DeCostePublisher:Cengage Learning General Chemistry - Standalone book (MindTap Cour...ChemistryISBN:9781305580343Author:Steven D. Gammon, Ebbing, Darrell Ebbing, Steven D., Darrell; Gammon, Darrell Ebbing; Steven D. Gammon, Darrell D.; Gammon, Ebbing; Steven D. Gammon; DarrellPublisher:Cengage Learning
General Chemistry - Standalone book (MindTap Cour...ChemistryISBN:9781305580343Author:Steven D. Gammon, Ebbing, Darrell Ebbing, Steven D., Darrell; Gammon, Darrell Ebbing; Steven D. Gammon, Darrell D.; Gammon, Ebbing; Steven D. Gammon; DarrellPublisher:Cengage Learning Chemistry & Chemical ReactivityChemistryISBN:9781337399074Author:John C. Kotz, Paul M. Treichel, John Townsend, David TreichelPublisher:Cengage Learning
Chemistry & Chemical ReactivityChemistryISBN:9781337399074Author:John C. Kotz, Paul M. Treichel, John Townsend, David TreichelPublisher:Cengage Learning Chemistry & Chemical ReactivityChemistryISBN:9781133949640Author:John C. Kotz, Paul M. Treichel, John Townsend, David TreichelPublisher:Cengage Learning
Chemistry & Chemical ReactivityChemistryISBN:9781133949640Author:John C. Kotz, Paul M. Treichel, John Townsend, David TreichelPublisher:Cengage Learning
 ChemistryChemistryISBN:9781305957404Author:Steven S. Zumdahl, Susan A. Zumdahl, Donald J. DeCostePublisher:Cengage Learning
ChemistryChemistryISBN:9781305957404Author:Steven S. Zumdahl, Susan A. Zumdahl, Donald J. DeCostePublisher:Cengage Learning

Introductory Chemistry: A Foundation
Chemistry
ISBN:9781337399425
Author:Steven S. Zumdahl, Donald J. DeCoste
Publisher:Cengage Learning

General Chemistry - Standalone book (MindTap Cour...
Chemistry
ISBN:9781305580343
Author:Steven D. Gammon, Ebbing, Darrell Ebbing, Steven D., Darrell; Gammon, Darrell Ebbing; Steven D. Gammon, Darrell D.; Gammon, Ebbing; Steven D. Gammon; Darrell
Publisher:Cengage Learning

Chemistry & Chemical Reactivity
Chemistry
ISBN:9781337399074
Author:John C. Kotz, Paul M. Treichel, John Townsend, David Treichel
Publisher:Cengage Learning

Chemistry & Chemical Reactivity
Chemistry
ISBN:9781133949640
Author:John C. Kotz, Paul M. Treichel, John Townsend, David Treichel
Publisher:Cengage Learning


Chemistry
Chemistry
ISBN:9781305957404
Author:Steven S. Zumdahl, Susan A. Zumdahl, Donald J. DeCoste
Publisher:Cengage Learning
Types of Matter: Elements, Compounds and Mixtures; Author: Professor Dave Explains;https://www.youtube.com/watch?v=dggHWvFJ8Xs;License: Standard YouTube License, CC-BY