
Concept explainers
It is a common practice when examining a fluid's viscous behavior to plot the shear strain rate (velocity gradient)
on the abscissa versus shear stress
where
For Bing hamplastics, the reis a yields tress
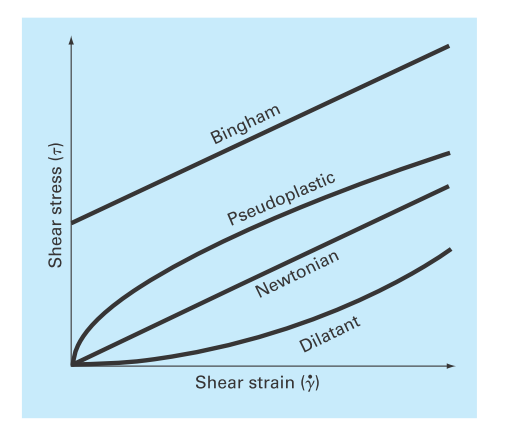
FIGURE P20.55
A common example is toothpaste.
For pseudoplastics, or “shear thinning” fluids, the shear stress is raised to a power n less than one,
Such fluids, such as yogurt, mayonnaise, and shampoo, exhibit a decrease in viscosity with increasing stress. Note that for cases where
The following data show the relationship be tween the shear stress
| Stress
|
3.25 | 4.25 | 4.65 | 5.65 | 6.05 |
| Shear strain rate
|
0.9 | 2.1 | 2.9 | 4.1 | 4.9 |
Want to see the full answer?
Check out a sample textbook solution
Chapter 20 Solutions
EBK NUMERICAL METHODS FOR ENGINEERS
- a=2, b=1 A bullet is to be tested in the laboratory to determine the drag force on it. Dependent parameter the drag force D (Newton) depends on the velocity of the bullet V(m/s), the length of the bullet L(m), sound velocity c(m/s), density of fluid ρ (kg/m3) and dynamic viscosity µ(kg/ms). Solve the problem by making the necessary assumptions and drawing the schematic figure I-Determine the nondimensional p parameters using repeating variables ii-a bullet with a speed of 9a,b m/s in air may be modelled in a water tunnel with a test section velocity of 2ab cm/s. Determine the length of the model, if the length of the bullet is 5a,b mm. The air and water temperature is 20 oC degree at 1 atm. iii- if the drag force on the model is measured to be 2,ab N, then determine the expected drag force on the bullet. Comment on dynamic similarity equivalence?arrow_forwardThe pressure drops 4P = P₁ P2 through a long section of round pipe can be written in terms of the shear stress Tw along the wall. Shown in Figure 3 is the shear stress acting by the wall on the fluid. The shaded region is a control volume composed of the fluid in the pipe between axial locations 1 and 2. Using the method of repeating variables, generate a relationship for pressure drop as a function of all other parameters Final ans AP = P μ (₁ AP= {(₂17₂) P₁ CV UPL м = (²1 ²² an! VPL O P.H. L Varrow_forwardAt any time, approximately 20 volcanoes are actively erupting on the Earth, and 50–70 volcanoes erupt each year. Over the past 100 years, an average of 850 people have died each year from volcano eruptions. As scientists and engineers study the mechanics of lava flow, accurately predicting the flow rate (velocity) of the lava is critical to saving lives after an eruption. Jeffrey’s equation captures the relationship between flow rate and viscosity as: where ρ is the density of the lava, g is gravity, t is the flow thickness, α is the slope, and m is the lava viscosity. Typical values are given as follows for the flow rate: m= 4x103 kg/(m.s) ±1% ρ= 2.5 g/cm3 ±1% t= 28 cm ±0.5 cm α= 10° ±1 ° g= 9.81 m/s²arrow_forward
- The modulus k of a coil spring (force required to stretch the spring a unit distance) can be expressed in equation form as k=(Gr^4)/(4R^3n) in which r and R are lengths and n is a dimensionless number. Determine the dimensions of G (a property of the spring material) .arrow_forwardAssignment 3 On Viscosity Calculation - Word TOUT REFERENCES MAILINGS REVIEW VIEW Hyperlink P Bookmark tArt Chart Screenshot Apps for Office Online Video Cross-reference Comment Header Footer Page Number Text Quick WordA Box Parts - ns Apps Media Links Comments Header & Footer (2) Referring to the following figure, the distance between plates is Ay = 0.5 cm, Av: = 10 cm/s, and the fluid is ethanol at 273 K having a viscosity of 1.77cp (0.0177 g/cm s). (a) Calculate the shear stress ty and the velocity (b) gradient of shear rate -/dy using cgs units. (c) Repeat using SI units. A Torce Fdshear berween teoparailel platesarrow_forwardThe friction in flows through the pipe is defined by a dimensionless number called the fanning friction factor (f). The Fanning friction factor is represented by another dimensionless number, the Reynolds number (Re).It depends on the diameter of the pipe and some parameters related to the fluid. An equation that can predict f given the Reynolds number is given as follows. If Re =4000, e/D=0.01 in this equation, find the value of f using the Simple Iteration method by taking f0=0.1 as the initial value for the solution (ԑ=0.0001)arrow_forward
- 1. Answer the following questions: (a) What is the physical meaning of the following: D a +V.v at Dt where V is the velocity vector of the flow field. (b) Let the viscous stress tensor be denoted by 7. How is the surface (vector) force f, acting by the fluid on a surface element ds (with unit normal în ) computed? Give your answer in vector notation and also in index notation. What is the physical meaning of Ty ? (c) Write down the work done on a material volume of fluid by the viscous surface force in vector notation and also in index notation. (d) Write down the amount of conduction heat flux 'q' (a scalar) on a surface element ds (with unit normal în ) in vector notation and also in index notation.arrow_forwardThe Reynolds number is a dimensionless group defined as follows for a liquid that flows through a pipe: Re = Dvρ / μ where D is the diameter of the pipe, v is the velocity of the fluid, ρ is its density and µ its viscosity. When the Reynolds number value is less than 2100, the flow is laminar, that is, the liquid it moves in lines of smooth flow. For Reynolds numbers greater than 2100, the flow is turbulent, characterized by considerable agitation. Liquid Methyl Ethyl Ketone (MEK) flows through 2067 '' ID tubing and through an average velocity of 0.48 ft / s. If the fluid temperature is 20 ° C, the density of the MEK The liquid is 0.805 g / cm and the viscosity is 0.43 cP (1 cP = 1.00 x 10 kg / (m-s)]. Determine the Reynolds number for MEK flow conditions. (Round the final result to a whole number without decimals).arrow_forwardA Newtonian fluid with absolute viscosity (Greek mu) flows past a flat surface. Due to the no-slip boundary condition, the velocity profile, u(y), develops near the surface and is given by u/U (shown in image provided) where the constant parameters U and delta have dimensions of velocity and length respectively.a) Develop an expression for the shear stress acting in any horizontal plane.b) Determine the shear stress acting on the surface at y = 0 and again at the edge of the boundarylayer, y = delta. (Express your answers in terms of Greek mu, the outer velocity U, and the boundary layer thickness delta.)arrow_forward
- fluıd mechanıcs Values for a fluid flowing in a circular pipe are given in the table.a) by writing Newton's law of viscosity,b) Determine the flow behavior of the fluids, show on the graph that they obey the Newtonian or non-Newtonian flow behavior. Calculate the dynamic viscosity values on the graph.c) If the viscosity of the liquid is 0.121 g/cm3, calculate the kinematic viscosity and convert it to the English Unit system.arrow_forward(Dimensional Analysis) If the velocity V in a fluid flow depends on a dimension 1, the fluid density p, and the viscosity µ, show that this implies that the Reynolds number Vlp/µ is constant.arrow_forwardCauchy's ΣF ) equation of motion : pDV/Dt =pg + VT (like pa Newtonian viscous stress relations by the tensor relation : Ti j = - pôij + µ[Əvj/əxi + əvi/axj] where dij is the kroneker delta function (1 for i = T includes pressure and viscous surface forces. into Cauchy's equation, and assume constant viscosity, to get the Navier-Stokes vector eq'ns : pDV/Dt Pg -vp + μ^2 V the acceleration DV/Dt av/at+ (VV)V, which for steady state flow gives DV/Dt =(V.) V. Because (VV) V is a non-linear term on the LHS of the N-S equation Reynolds Number RepVL/μ, a measure of the ratio of inertial to viscous forces. : Patm 10^5 = = N = N = ; pwater 1000; pair 1.2; μwater 10^-3 N s/m^2 ; Hair 2 x 10^-5 N•s/m^2 ; g 9.8 m/s^2 = j; 0 for i j ); Narrow_forward
 Elements Of ElectromagneticsMechanical EngineeringISBN:9780190698614Author:Sadiku, Matthew N. O.Publisher:Oxford University Press
Elements Of ElectromagneticsMechanical EngineeringISBN:9780190698614Author:Sadiku, Matthew N. O.Publisher:Oxford University Press Mechanics of Materials (10th Edition)Mechanical EngineeringISBN:9780134319650Author:Russell C. HibbelerPublisher:PEARSON
Mechanics of Materials (10th Edition)Mechanical EngineeringISBN:9780134319650Author:Russell C. HibbelerPublisher:PEARSON Thermodynamics: An Engineering ApproachMechanical EngineeringISBN:9781259822674Author:Yunus A. Cengel Dr., Michael A. BolesPublisher:McGraw-Hill Education
Thermodynamics: An Engineering ApproachMechanical EngineeringISBN:9781259822674Author:Yunus A. Cengel Dr., Michael A. BolesPublisher:McGraw-Hill Education Control Systems EngineeringMechanical EngineeringISBN:9781118170519Author:Norman S. NisePublisher:WILEY
Control Systems EngineeringMechanical EngineeringISBN:9781118170519Author:Norman S. NisePublisher:WILEY Mechanics of Materials (MindTap Course List)Mechanical EngineeringISBN:9781337093347Author:Barry J. Goodno, James M. GerePublisher:Cengage Learning
Mechanics of Materials (MindTap Course List)Mechanical EngineeringISBN:9781337093347Author:Barry J. Goodno, James M. GerePublisher:Cengage Learning Engineering Mechanics: StaticsMechanical EngineeringISBN:9781118807330Author:James L. Meriam, L. G. Kraige, J. N. BoltonPublisher:WILEY
Engineering Mechanics: StaticsMechanical EngineeringISBN:9781118807330Author:James L. Meriam, L. G. Kraige, J. N. BoltonPublisher:WILEY





