Math
CalculusCalculus (MindTap Course List)31-32 The graph of the derivative f ′ of a continuous function f is shown. (a) On what intervals is f increasing? Decreasing? (b) At what values of x does f have a local maximum? Local minimum? (c) On what intervals is f concave upward? Concave downward? (d) State the x -coordinate(s) of the point(s) of inflection. (e) Assuming that f ( 0 ) = 0 , sketch a graph of f .

31-32 The graph of the derivative f ′ of a continuous function f is shown. (a) On what intervals is f increasing? Decreasing? (b) At what values of x does f have a local maximum? Local minimum? (c) On what intervals is f concave upward? Concave downward? (d) State the x -coordinate(s) of the point(s) of inflection. (e) Assuming that f ( 0 ) = 0 , sketch a graph of f .

BuyFind

Calculus (MindTap Course List)

8th Edition
James Stewart
Publisher: Cengage Learning
ISBN: 9781285740621
BuyFind

Calculus (MindTap Course List)

8th Edition
James Stewart
Publisher: Cengage Learning
ISBN: 9781285740621

Solutions

Chapter
Section
Problem 1E
Problem 2E
Problem 3E
Problem 4E
Problem 5E
Problem 6E
Problem 7E
Problem 8E
Problem 9E
Problem 10E
Problem 11E
Problem 12E
Problem 13E
Problem 14E
Problem 15E
Problem 16E
Problem 17E
Problem 18E
Problem 19E
Problem 20E
Problem 21E
Problem 22E
Problem 23E
Problem 24E
Problem 25E
Problem 26E
Problem 27E
Problem 28E
Problem 29E
Problem 30E
Problem 31E
Problem 32E
Problem 33E
Problem 34E
Problem 35E
Problem 36E
Problem 37E
Problem 38E
Problem 39E
Problem 40E
Problem 41E
Problem 42E
Problem 43E
Problem 44E
Problem 45E
Problem 46E
Problem 47E
Problem 48E
Problem 49E
Problem 50E
Problem 51E
Problem 52E
Problem 53E
Problem 54E
Problem 55E
Problem 56E
Problem 57E
Problem 58E
Problem 59E
Problem 60E
Problem 61E
Problem 62E
Problem 63E
Problem 64E
Problem 65E
Problem 66E
Problem 67E
Problem 68E
Problem 69E
Problem 70E
Problem 71E
Problem 72E
Problem 73E
Problem 74E
Problem 75E
Problem 76E
Problem 77E
Chapter 3.3, Problem 31E
Textbook Problem

31-32 The graph of the derivative f′ of a continuous function f is shown.

(a) On what intervals is f increasing? Decreasing?

(b) At what values of x does f have a local maximum? Local minimum?

(c) On what intervals is f concave upward? Concave downward?

(d) State the x-coordinate(s) of the point(s) of inflection.

(e) Assuming that f ( 0 ) = 0 , sketch a graph of f.

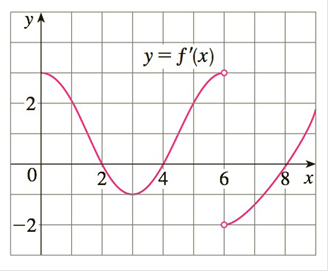
Chapter 3.3, Problem 31E, 31-32 The graph of the derivative f of a continuous function f is shown. a On what intervals is f

Expert Solution

Want to see the full answer?

Check out a sample textbook solution.
Chapter 3.3,
Problem 30E
Chapter 3.3,
Problem 32E

Want to see this answer and more?

Experts are waiting 24/7 to provide step-by-step solutions in as fast as 30 minutes!*

*Response times vary by subject and question complexity. Median response time is 34 minutes and may be longer for new subjects.

Chapter 3 Solutions

Calculus (MindTap Course List)
Ch. 3.1 - Explain the difference between an absolute minimum...Ch. 3.1 - Suppose f is a continuous function defined on a...Ch. 3.1 - For each of the numbers a, b, c, d, r, and s,...Ch. 3.1 - For each of the numbers a, b, c, d, r, and s,...Ch. 3.1 - Use the graph to state the absolute and local...Ch. 3.1 - Use the graph to state the absolute and local...Ch. 3.1 - Sketch the graph of a function f that is...Ch. 3.1 - Sketch the graph of a function f that is...Ch. 3.1 - Sketch the graph of a function f that is...Ch. 3.1 - Sketch the graph of a function f that is...
Ch. 3.1 - a Sketch the graph of a function that has a local...Ch. 3.1 - a Sketch the graph of a function on [1,2] that has...Ch. 3.1 - a Sketch the graph of a function on [1,2] that has...Ch. 3.1 - a Sketch the graph of a function that has two...Ch. 3.1 - Sketch the graph of f by hand and use your sketch...Ch. 3.1 - Sketch the graph of f by hand and use your sketch...Ch. 3.1 - Sketch the graph of f by hand and use your sketch...Ch. 3.1 - Sketch the graph of f by hand and use your sketch...Ch. 3.1 - Sketch the graph of f by hand and use your sketch...Ch. 3.1 - Sketch the graph of f by hand and use your sketch...Ch. 3.1 - Sketch the graph of f by hand and use your sketch...Ch. 3.1 - Sketch the graph of f by hand and use your sketch...Ch. 3.1 - Sketch the graph of f by hand and use your sketch...Ch. 3.1 - Sketch the graph of f by hand and use your sketch...Ch. 3.1 - Sketch the graph of f by hand and use your sketch...Ch. 3.1 - Sketch the graph of f by hand and use your sketch...Ch. 3.1 - Sketch the graph of f by hand and use your sketch...Ch. 3.1 - Sketch the graph of f by hand and use your sketch...Ch. 3.1 - Find the critical numbers of the function....Ch. 3.1 - Find the critical numbers of the function....Ch. 3.1 - Find the critical numbers of the function....Ch. 3.1 - Find the critical numbers of the function....Ch. 3.1 - Find the critical numbers of the function....Ch. 3.1 - Find the critical numbers of the function....Ch. 3.1 - Find the critical numbers of the function....Ch. 3.1 - Find the critical numbers of the function....Ch. 3.1 - Find the critical numbers of the function....Ch. 3.1 - Find the critical numbers of the function....Ch. 3.1 - Find the critical numbers of the function....Ch. 3.1 - Find the critical numbers of the function....Ch. 3.1 - Find the critical numbers of the function....Ch. 3.1 - Find the critical numbers of the function....Ch. 3.1 - A formula for the derivative of a function f is...Ch. 3.1 - A formula for the derivative of a function f is...Ch. 3.1 - Find the absolute maximum and absolute minimum...Ch. 3.1 - Find the absolute maximum and absolute minimum...Ch. 3.1 - Find the absolute maximum and absolute minimum...Ch. 3.1 - Find the absolute maximum and absolute minimum...Ch. 3.1 - Find the absolute maximum and absolute minimum...Ch. 3.1 - Find the absolute maximum and absolute minimum...Ch. 3.1 - Find the absolute maximum and absolute minimum...Ch. 3.1 - Find the absolute maximum and absolute minimum...Ch. 3.1 - Find the absolute maximum and absolute minimum...Ch. 3.1 - Find the absolute maximum and absolute minimum...Ch. 3.1 - Find the absolute maximum and absolute minimum...Ch. 3.1 - Find the absolute maximum and absolute minimum...Ch. 3.1 - If a and b are positive numbers, find the maximum...Ch. 3.1 - Use a graph to estimate the critical numbers of...Ch. 3.1 - a Use a graph to estimate the absolute maximum and...Ch. 3.1 - a Use a graph to estimate the absolute maximum and...Ch. 3.1 - a Use a graph to estimate the absolute maximum and...Ch. 3.1 - a Use a graph to estimate the absolute maximum and...Ch. 3.1 - Between 0C and 30C, the volume V in cubic...Ch. 3.1 - An object with weight W is dragged along a...Ch. 3.1 - The water level, measured in feet above mean sea...Ch. 3.1 - On May 7, 1992, the space shuttle Endeavour was...Ch. 3.1 - When a foreign object lodged in the trachea...Ch. 3.1 - Show that 5 is a critical number of the function...Ch. 3.1 - Prove that the function f(x)=x101+x51+x+1 has...Ch. 3.1 - If f has a local minimum value at c, show that the...Ch. 3.1 - Prove Fermats Theorem for the case in which f has...Ch. 3.1 - A cubic function is a polynomial of degree 3; that...Ch. 3.2 - The graph of a function f is shown. Verify that f...Ch. 3.2 - Draw the graph of a function defined on 0, 8 such...Ch. 3.2 - The graph of a function g is shown. a Verify that...Ch. 3.2 - Draw the graph of a function that is continuous on...Ch. 3.2 - 5-8 Verify that the function satisfies the three...Ch. 3.2 - 5-8 Verify that the function satisfies the three...Ch. 3.2 - 5-8 Verify that the function satisfies the three...Ch. 3.2 - 5-8 Verify that the function satisfies the three...Ch. 3.2 - Let f(x)=1x2/3. Show that f(1)=f(1) but there is...Ch. 3.2 - Let f(x)=tanx. Show that f(0)=f() but there is no...Ch. 3.2 - 11-14 Verify that the function satisfies the...Ch. 3.2 - 11-14 Verify that the function satisfies the...Ch. 3.2 - 11-14 Verify that the function satisfies the...Ch. 3.2 - 11-14 Verify that the function satisfies the...Ch. 3.2 - 15-16 Find the number c that satisfies the...Ch. 3.2 - 15-16 Find the number c that satisfies the...Ch. 3.2 - Let f(x)=(x3)2. Show that there is no value of c...Ch. 3.2 - Let f(x)=2|2x1|. Show that there is no value of c...Ch. 3.2 - 19-20 Show that the equation has exactly one real...Ch. 3.2 - 19-20 Show that the equation has exactly one real...Ch. 3.2 - Show that the equation x315x+c=0 has at most one...Ch. 3.2 - Show that the equation x4+4x+c=0 has at most two...Ch. 3.2 - a Show that a polynomial of degree 3 has at most...Ch. 3.2 - a Suppose that f is differentiable on and has two...Ch. 3.2 - If f(1)=10 and f(x)2 for 1x4, how small can f(4)...Ch. 3.2 - Suppose that 3f(x)5 for all values of x. Show that...Ch. 3.2 - Does there exist a function f such that...Ch. 3.2 - Suppose that f and g are continuous on a, b and...Ch. 3.2 - Show that sinxxif0x2.Ch. 3.2 - Suppose f is an odd function and is differentiable...Ch. 3.2 - Use the Mean Value Theorem to prove the inequality...Ch. 3.2 - If f(x)=c c a constant for all x, use Corollary to...Ch. 3.2 - Let f(x)=1/x and g(x)={1xifx01+1xifx0 Show that...Ch. 3.2 - At 2:00 pm a cars speedometer reads 30 mi/h. At...Ch. 3.2 - Two runners start a race at the same time and...Ch. 3.2 - A number a is called a fixed point of a function f...Ch. 3.3 - 1-2 Use the given graph of f to find the...Ch. 3.3 - 1-2 Use the given graph of f to find the...Ch. 3.3 - Suppose you are given a formula for a function f....Ch. 3.3 - a State the First Derivative Test. b State the...Ch. 3.3 - 5-6 The graph of the derivative f of a function f...Ch. 3.3 - 5-6 The graph of the derivative f of a function f...Ch. 3.3 - In each part state the x-coordinates of the...Ch. 3.3 - The graph of the first derivative f of a function...Ch. 3.3 - 9-14 a Find the intervals on which f is increasing...Ch. 3.3 - 9-14 a Find the intervals on which f is increasing...Ch. 3.3 - 9-14 a Find the intervals on which f is increasing...Ch. 3.3 - 9-14 a Find the intervals on which f is increasing...Ch. 3.3 - 9-14 a Find the intervals on which f is increasing...Ch. 3.3 - 9-14 a Find the intervals on which f is increasing...Ch. 3.3 - 15-17 Find the local maximum and minimum values of...Ch. 3.3 - 15-17 Find the local maximum and minimum values of...Ch. 3.3 - 15-17 Find the local maximum and minimum values of...Ch. 3.3 - a Find the critical numbers of f(x)=x4(x1)3. b...Ch. 3.3 - Suppose f" is continuous on (,). a If f2 = 0 and...Ch. 3.3 - 20-27 Sketch the graph of a function that...Ch. 3.3 - 20-27 Sketch the graph of a function that...Ch. 3.3 - 20-27 Sketch the graph of a function that...Ch. 3.3 - 20-27 Sketch the graph of a function that...Ch. 3.3 - 20-27 Sketch the graph of a function that...Ch. 3.3 - 20-27 Sketch the graph of a function that...Ch. 3.3 - 20-27 Sketch the graph of a function that...Ch. 3.3 - 20-27 Sketch the graph of a function that...Ch. 3.3 - Suppose f(3)=2,f(3)=12, and f(x)0 and f(x)0 for...Ch. 3.3 - Suppose f is a continuous function where f(x)0 for...Ch. 3.3 - The graph of a function y=f(x) is shown. At which...Ch. 3.3 - 31-32 The graph of the derivative f of a...Ch. 3.3 - 31-32 The graph of the derivative f of a...Ch. 3.3 - 33-44 a Find the intervals of increase or...Ch. 3.3 - 33-44 a Find the intervals of increase or...Ch. 3.3 - 33-44 a Find the intervals of increase or...Ch. 3.3 - 33-44 a Find the intervals of increase or...Ch. 3.3 - 33-44 a Find the intervals of increase or...Ch. 3.3 - 33-44 a Find the intervals of increase or...Ch. 3.3 - 33-44 a Find the intervals of increase or...Ch. 3.3 - 33-44 a Find the intervals of increase or...Ch. 3.3 - 33-44 a Find the intervals of increase or...Ch. 3.3 - 33-44 a Find the intervals of increase or...Ch. 3.3 - 33-44 a Find the intervals of increase or...Ch. 3.3 - 33-44 a Find the intervals of increase or...Ch. 3.3 - Suppose the derivative of a function f is...Ch. 3.3 - Use the methods of this section to sketch the...Ch. 3.3 - 47-48 a Use a graph of f to estimate the maximum...Ch. 3.3 - 47-48 a Use a graph of f to estimate the maximum...Ch. 3.3 - 49-50 a Use a graph of f to give a rough estimate...Ch. 3.3 - 49-50 a Use a graph of / to give a rough estimate...Ch. 3.3 - 51-52 Estimate the intervals of concavity to one...Ch. 3.3 - 51-52 Estimate the intervals of concavity to one...Ch. 3.3 - A graph of a population of yeast cells in a new...Ch. 3.3 - In an episode of The Simpsons television show,...Ch. 3.3 - The president announces that the national deficit...Ch. 3.3 - Let f(t) be the temperature at time t where you...Ch. 3.3 - Let Kt be a measure of the knowledge you gain by...Ch. 3.3 - Coffee is being poured into the mug shown in the...Ch. 3.3 - Lind a cubic function f(x)=ax3+bx2+cx+d that has a...Ch. 3.3 - Show that the curve y=1+x1+x2 has three points of...Ch. 3.3 - a If the function f(x)=x3+ax2+bx has the local...Ch. 3.3 - For what values of a and b is 2, 2.5 an inflection...Ch. 3.3 - Show that the inflection points of the curve...Ch. 3.3 - 64-66 Assume that all of the functions are twice...Ch. 3.3 - 64-66 Assume that all of the functions are twice...Ch. 3.3 - 64-66 Assume that all of the functions are twice...Ch. 3.3 - Show that tanxfor0x/2. Hint: Show that f(x)=tanxx...Ch. 3.3 - Prove that, for all x1, 2x31xCh. 3.3 - Show that a cubic function a third-degree...Ch. 3.3 - For what values of c does the polynomial...Ch. 3.3 - Prove that if (c,f(c)) is a point of inflection of...Ch. 3.3 - Show that if f(x)=x4, then f(0)=0, but 0, 0 is not...Ch. 3.3 - Show that the function g(x)=x|x| has an inflection...Ch. 3.3 - Suppose that f is continuous and f(c)=f(c)=0, but...Ch. 3.3 - Suppose f is differentiable on an interval I and...Ch. 3.3 - For what values of c is the function f(x)=cx+1x2+3...Ch. 3.3 - The three cases in the First Derivative Test cover...Ch. 3.4 - Explain in your own words the meaning of each of...Ch. 3.4 - a Can the graph of y=f(x) intersect a vertical...Ch. 3.4 - For the function f whose graph is given, state the...Ch. 3.4 - For the function g whose graph is given, state the...Ch. 3.4 - Guess the value of the limit limxx22x be...Ch. 3.4 - a Use a graph of f(x)=(12x)x to estimate the value...Ch. 3.4 - 7-8 Evaluate the limit and justify each step by...Ch. 3.4 - 7-8 Evaluate the limit and justify each step by...Ch. 3.4 - 9-32 Find the limit or show that it does not...Ch. 3.4 - 9-32 Find the limit or show that it does not...Ch. 3.4 - 9-32 Find the limit or show that it does not...Ch. 3.4 - 9-32 Find the limit or show that it does not...Ch. 3.4 - 9-32 Find the limit or show that it does not...Ch. 3.4 - 9-32 Find the limit or show that it does not...Ch. 3.4 - 9-32 Find the limit or show that it does not...Ch. 3.4 - 9-32 Find the limit or show that it does not...Ch. 3.4 - 9-32 Find the limit or show that it does not...Ch. 3.4 - 9-32 Find the limit or show that it does not...Ch. 3.4 - 9-32 Find the limit or show that it does not...Ch. 3.4 - 9-32 Find the limit or show that it does not...Ch. 3.4 - 9-32 Find the limit or show that it does not...Ch. 3.4 - 9-32 Find the limit or show that it does not...Ch. 3.4 - 9-32 Find the limit or show that it does not...Ch. 3.4 - 9-32 Find the limit or show that it does not...Ch. 3.4 - 9-32 Find the limit or show that it does not...Ch. 3.4 - 9-32 Find the limit or show that it does not...Ch. 3.4 - 9-32 Find the limit or show that it does not...Ch. 3.4 - 9-32 Find the limit or show that it does not...Ch. 3.4 - 9-32 Find the limit or show that it does not...Ch. 3.4 - 9-32 Find the limit or show that it does not...Ch. 3.4 - 9-32 Find the limit or show that it does not...Ch. 3.4 - 9-32 Find the limit or show that it does not...Ch. 3.4 - a Estimate the value of limx(x2+x+1+x) by graphing...Ch. 3.4 - a Use a graph of f(x)=3x2+8x+63x2+3x+1 to estimate...Ch. 3.4 - 35-40 Find the horizontal and vertical asymptotes...Ch. 3.4 - 35-40 Find the horizontal and vertical asymptotes...Ch. 3.4 - 35-40 Find the horizontal and vertical asymptotes...Ch. 3.4 - 35-40 Find the horizontal and vertical asymptotes...Ch. 3.4 - 35-40 Find the horizontal and vertical asymptotes...Ch. 3.4 - 35-40 Find the horizontal and vertical asymptotes...Ch. 3.4 - Estimate the horizontal asymptote of the function...Ch. 3.4 - a Graph the function f(x)=2x2+13x5 How many...Ch. 3.4 - Let P and Q be polynomials. Find limxP(x)Q(x) if...Ch. 3.4 - Make a rough sketch of the curve y=xn n an integer...Ch. 3.4 - Find a formula for a function / that satisfies the...Ch. 3.4 - Find a formula for a function that has vertical...Ch. 3.4 - A function f is a ratio of quadratic functions and...Ch. 3.4 - 48-51 Find the horizontal asymptotes of the curve...Ch. 3.4 - 48-51 Find the horizontal asymptotes of the curve...Ch. 3.4 - 48-51 Find the horizontal asymptotes of the curve...Ch. 3.4 - 48-51 Find the horizontal asymptotes of the curve...Ch. 3.4 - 52-56 Find the limits as x and as x. Use this...Ch. 3.4 - 52-56 Find the limits as x and as x. Use this...Ch. 3.4 - 52-56 Find the limits as x and as x. Use this...Ch. 3.4 - 52-56 Find the limits as x and as x. Use this...Ch. 3.4 - 52-56 Find the limits as x and as x. Use this...Ch. 3.4 - 57-60 Sketch the graph of a function that...Ch. 3.4 - 57-60 Sketch the graph of a function that...Ch. 3.4 - 57-60 Sketch the graph of a function that...Ch. 3.4 - 57-60 Sketch the graph of a function that...Ch. 3.4 - a Use the Squeeze Theorem to evaluate limxsinxx. b...Ch. 3.4 - By the end behavior of a function we mean the...Ch. 3.4 - Find limxf(x) if 4x1xf(x)4x2+3xx2 for all x5.Ch. 3.4 - a A tank contains 5000 L of pure water. Brine that...Ch. 3.4 - Use a graph to find a number N such that...Ch. 3.4 - For the limit limx13xx2+1=3 illustrate Definition...Ch. 3.4 - For the limit limx13xx2+1=3 illustrate Definition...Ch. 3.4 - For the limit limx3xx3= illustrate Definition 7 by...Ch. 3.4 - a How large do we have to take x so that...Ch. 3.4 - a How large do we have to take x so that...Ch. 3.4 - Use Definition 6 to prove that limx1x=0Ch. 3.4 - Prove, using Definition 7, that limxx3=Ch. 3.4 - a Prove that limxf(x)=limt0+f(1/t) and...Ch. 3.4 - Formulate a precise definition of limxf(x)= Then...Ch. 3.5 - 1-40 Use the guidelines of this section to sketch...Ch. 3.5 - 1-40 Use the guidelines of this section to sketch...Ch. 3.5 - 1-40 Use the guidelines of this section to sketch...Ch. 3.5 - 1-40 Use the guidelines of this section to sketch...Ch. 3.5 - 1-40 Use the guidelines of this section to sketch...Ch. 3.5 - 1-40 Use the guidelines of this section to sketch...Ch. 3.5 - 1-40 Use the guidelines of this section to sketch...Ch. 3.5 - 1-40 Use the guidelines of this section to sketch...Ch. 3.5 - 1-40 Use the guidelines of this section to sketch...Ch. 3.5 - 1-40 Use the guidelines of this section to sketch...Ch. 3.5 - 1-40 Use the guidelines of this section to sketch...Ch. 3.5 - 1-40 Use the guidelines of this section to sketch...Ch. 3.5 - 1-40 Use the guidelines of this section to sketch...Ch. 3.5 - 1-40 Use the guidelines of this section to sketch...Ch. 3.5 - 1-40 Use the guidelines of this section to sketch...Ch. 3.5 - 1-40 Use the guidelines of this section to sketch...Ch. 3.5 - 1-40 Use the guidelines of this section to sketch...Ch. 3.5 - 1-40 Use the guidelines of this section to sketch...Ch. 3.5 - 1-40 Use the guidelines of this section to sketch...Ch. 3.5 - 1-40 Use the guidelines of this section to sketch...Ch. 3.5 - 1-40 Use the guidelines of this section to sketch...Ch. 3.5 - 1-40 Use the guidelines of this section to sketch...Ch. 3.5 - 1-40 Use the guidelines of this section to sketch...Ch. 3.5 - 1-40 Use the guidelines of this section to sketch...Ch. 3.5 - 1-40 Use the guidelines of this section to sketch...Ch. 3.5 - 1-40 Use the guidelines of this section to sketch...Ch. 3.5 - 1-40 Use the guidelines of this section to sketch...Ch. 3.5 - 1-40 Use the guidelines of this section to sketch...Ch. 3.5 - 1-40 Use the guidelines of this section to sketch...Ch. 3.5 - 1-40 Use the guidelines of this section to sketch...Ch. 3.5 - 1-40 Use the guidelines of this section to sketch...Ch. 3.5 - 1-40 Use the guidelines of this section to sketch...Ch. 3.5 - 1-40 Use the guidelines of this section to sketch...Ch. 3.5 - 1-40 Use the guidelines of this section to sketch...Ch. 3.5 - 1-40 Use the guidelines of this section to sketch...Ch. 3.5 - 1-40 Use the guidelines of this section to sketch...Ch. 3.5 - 1-40 Use the guidelines of this section to sketch...Ch. 3.5 - 1-40 Use the guidelines of this section to sketch...Ch. 3.5 - 1-40 Use the guidelines of this section to sketch...Ch. 3.5 - 1-40 Use the guidelines of this section to sketch...Ch. 3.5 - In the theory of relativity, the mass of a...Ch. 3.5 - In the theory of relativity, the energy of a...Ch. 3.5 - The figure shows a beam of length L embedded in...Ch. 3.5 - Coulombs Law states that the force of attraction...Ch. 3.5 - 4548 Find an equation of the slant asymptote. Do...Ch. 3.5 - 4548 Find an equation of the slant asymptote. Do...Ch. 3.5 - 4548 Find an equation of the slant asymptote. Do...Ch. 3.5 - 4548. Find an equation of the slant asymptote. Do...Ch. 3.5 - 4954 Use the guidelines of this section to sketch...Ch. 3.5 - 4954 Use the guidelines of this section to sketch...Ch. 3.5 - 4954 Use the guidelines of this section to sketch...Ch. 3.5 - 4954 Use the guidelines of this section to sketch...Ch. 3.5 - 4954 Use the guidelines of this section to sketch...Ch. 3.5 - 4954 Use the guidelines of this section to sketch...Ch. 3.5 - Show that the curve y=4x2+9 has two slant...Ch. 3.5 - Show that the curve y=x2+4x has two slant...Ch. 3.5 - Show that the lines y=(b/a)x and y=(b/a)x are...Ch. 3.5 - Let f(x)=(x3+1)/x. Show that limx[f(x)x2]=0 This...Ch. 3.5 - Discuss the asymptotic behavior of f(x)=x4+1x in...Ch. 3.5 - Use the asymptotic behavior of f(x)=cosx+1/x2 to...Ch. 3.6 - 18 Produce graphs of f that reveal all the...Ch. 3.6 - 18 Produce graphs of f that reveal all the...Ch. 3.6 - 18 Produce graphs of f that reveal all the...Ch. 3.6 - 18 Produce graphs of f that reveal all the...Ch. 3.6 - 18 Produce graphs of f that reveal all the...Ch. 3.6 - 18 Produce graphs of f that reveal all the...Ch. 3.6 - 18 Produce graphs of f that reveal all the...Ch. 3.6 - 18 Produce graphs of f that reveal all the...Ch. 3.6 - 910 Produce graphs of f that reveal all the...Ch. 3.6 - 910 Produce graphs of f that reveal all the...Ch. 3.6 - 1112 Sketch the graph by hand using asymptotes and...Ch. 3.6 - 1112 Sketch the graph by hand using asymptotes and...Ch. 3.6 - If f is the function considered in Example 3, use...Ch. 3.6 - If f is the function of Exercise 12, find f and f"...Ch. 3.6 - 1518 Use a computer algebra system to graph f and...Ch. 3.6 - 1518 Use a computer algebra system to graph f and...Ch. 3.6 - 1518 Use a computer algebra system to graph f and...Ch. 3.6 - 1518 Use a computer algebra system to graph f and...Ch. 3.6 - In Example 4 we considered a member of the family...Ch. 3.6 - 2025 Describe how the graph of f varies as c...Ch. 3.6 - 2025 Describe how the graph of f varies as c...Ch. 3.6 - 2025 Describe how the graph of f varies as c...Ch. 3.6 - 2025 Describe how the graph of f varies as c...Ch. 3.6 - 2025 Describe how the graph of f varies as c...Ch. 3.6 - 2025 Describe how the graph of f varies as c...Ch. 3.6 - Investigate the family of curves given by the...Ch. 3.6 - a Investigate the family of polynomials given by...Ch. 3.6 - a Investigate the family of polynomials given by...Ch. 3.7 - Consider the following problem: Find two numbers...Ch. 3.7 - Find two numbers whose difference is 100 and whose...Ch. 3.7 - Find two positive numbers whose product is 100 and...Ch. 3.7 - The sum of two positive numbers is 16. What is the...Ch. 3.7 - What is the maximum vertical distance between the...Ch. 3.7 - What is the minimum vertical distance between the...Ch. 3.7 - Find the dimensions of a rectangle with perimeter...Ch. 3.7 - Find the dimensions of a rectangle with area 1000...Ch. 3.7 - A model used for the yield y of an agricultural...Ch. 3.7 - The rate in mg carbon/m3/h at which photosynthesis...Ch. 3.7 - Consider the following problem: A farmer with 750...Ch. 3.7 - Consider the following problem: A box with an open...Ch. 3.7 - A farmer wants to fence in an area of 1.5 million...Ch. 3.7 - A box with a square base and open top must have a...Ch. 3.7 - If 1200 cm2 of material is available to make a box...Ch. 3.7 - A rectangular storage container with an open top...Ch. 3.7 - Do Exercise 16 assuming the container has a fid...Ch. 3.7 - A farmer wants to fence in a rectangular plot of...Ch. 3.7 - If the farmer in Exercise 18 wants to enclose 8000...Ch. 3.7 - a Show that of all the rectangles with a given...Ch. 3.7 - Find the point on the line y=2x+3 that is closest...Ch. 3.7 - Find the point on the curve y=x that is closest to...Ch. 3.7 - Find the points on the ellipse 4x2+y2=4 that are...Ch. 3.7 - Find, correct to two decimal places, the...Ch. 3.7 - Find the dimensions of the rectangle of largest...Ch. 3.7 - Find the area of the largest rectangle that can be...Ch. 3.7 - Find the dimensions of the rectangle of largest...Ch. 3.7 - Find the area of the largest trapezoid that can be...Ch. 3.7 - Find the dimensions of the isosceles triangle of...Ch. 3.7 - If the two equal sides of an isosceles triangle...Ch. 3.7 - A right circular cylinder is inscribed in a sphere...Ch. 3.7 - A right circular cylinder is inscribed in a cone...Ch. 3.7 - A right circular cylinder is inscribed in a sphere...Ch. 3.7 - A Norman window has the shape of a rectangle...Ch. 3.7 - The top and bottom margins of a poster are each 6...Ch. 3.7 - A poster is to have an area of 180 in 2 with...Ch. 3.7 - A piece of wire 10 m long is cut into two pieces....Ch. 3.7 - Solve Exercise 37 if one piece is bent into a...Ch. 3.7 - If you are offered one slice from a round pizza in...Ch. 3.7 - A fence 8 ft tall runs parallel to a tall building...Ch. 3.7 - A cone-shaped drinking cup is made from a circular...Ch. 3.7 - A cone-shaped paper drinking cup is to be made to...Ch. 3.7 - A cone with height h is inscribed in a larger cone...Ch. 3.7 - An object with weight W is dragged along a...Ch. 3.7 - If a resistor of R ohms is connected across a...Ch. 3.7 - For a fish swimming at a speed v relative to the...Ch. 3.7 - In a beehive, each cell is a regular hexagonal...Ch. 3.7 - A boat leaves a dock at 2:00 PM and travels due...Ch. 3.7 - Solve the problem in Example 4 if the river is 5...Ch. 3.7 - A woman at a point A on the shore of a circular...Ch. 3.7 - An oil refinery is located on the north bank of a...Ch. 3.7 - Suppose the refinery in Exercise 51 is located 1...Ch. 3.7 - The illumination of an object by a fight source is...Ch. 3.7 - Find an equation of the line through the point 3,...Ch. 3.7 - Let a and b be positive numbers. Find the length...Ch. 3.7 - At which points on the curve y=1+40x33x5 does the...Ch. 3.7 - What is the shortest possible length of the line...Ch. 3.7 - What is the smallest possible area of the triangle...Ch. 3.7 - a If C(x) is the cost of producing x units of a...Ch. 3.7 - a Show that if the profit p(x) is a maximum, then...Ch. 3.7 - A baseball team plays in a stadium that holds...Ch. 3.7 - During the summer months Terry makes and sells...Ch. 3.7 - A retailer has been selling 1200 tablet computers...Ch. 3.7 - A company operates 16 oil wells in a designated...Ch. 3.7 - Show that of all the isosceles triangles with a...Ch. 3.7 - Consider the situation in Exercise 51 if the cost...Ch. 3.7 - Consider the tangent line to the ellipse...Ch. 3.7 - The frame for a kite is to be made from six pieces...Ch. 3.7 - A point P needs to be located somewhere on the...Ch. 3.7 - The graph shows the fuel consumption c of a car...Ch. 3.7 - Let v1 be the velocity of light in air and v2 the...Ch. 3.7 - Two vertical poles PQ and ST are secured by a rope...Ch. 3.7 - The upper right-hand corner of a piece of paper,...Ch. 3.7 - A steel pipe is being carried down a hallway 9 ft...Ch. 3.7 - An observer stands at a point P, one unit away...Ch. 3.7 - A rain gutter is to be constructed from a metal...Ch. 3.7 - Find the maximum area of a rectangle that can be...Ch. 3.7 - The blood vascular system consists of blood...Ch. 3.7 - Ornithologists have determined that some species...Ch. 3.7 - Two light sources of identical strength are placed...Ch. 3.8 - The figure shows the graph of a function f....Ch. 3.8 - Follow the instructions for Exercise 1a but use...Ch. 3.8 - Suppose the tangent line to the curve y=f(x) at...Ch. 3.8 - For each initial approximation, determine...Ch. 3.8 - For which of the initial approximations x1=a,b,c,...Ch. 3.8 - 6-8 Use Newtons method with the specified initial...Ch. 3.8 - 6-8 Use Newtons method with the specified initial...Ch. 3.8 - 6-8 Use Newtons method with the specified initial...Ch. 3.8 - Use Newtons method with initial approximation x1=1...Ch. 3.8 - Use Newtons method with initial approximation x1=1...Ch. 3.8 - 11-12 Use Newtons method to approximate the given...Ch. 3.8 - 11-12 Use Newtons method to approximate the given...Ch. 3.8 - 13-14 a Explain how we know that the given...Ch. 3.8 - 13-14 a Explain how we know that the given...Ch. 3.8 - 15-16 Use Newtons method to approximate the...Ch. 3.8 - 15-16 Use Newtons method to approximate the...Ch. 3.8 - 17-22 Use Newtons method to find all solutions of...Ch. 3.8 - 17-22 Use Newtons method to find all solutions of...Ch. 3.8 - 17-22 Use Newtons method to find all solutions of...Ch. 3.8 - 17-22 Use Newtons method to find all solutions of...Ch. 3.8 - 17-22 Use Newtons method to find all solutions of...Ch. 3.8 - 17-22 Use Newtons method to find all solutions of...Ch. 3.8 - 23-26 Use Newtons method to find all the solutions...Ch. 3.8 - 23-26 Use Newtons method to find all the solutions...Ch. 3.8 - 23-26 Use Newtons method to find all the solutions...Ch. 3.8 - 23-26 Use Newtons method to find all the solutions...Ch. 3.8 - a Apply Newtons method to the equation x2a=0 to...Ch. 3.8 - a Apply Newtons method to the equation 1/xa=0 to...Ch. 3.8 - Explain why Newtons method doesnt work for finding...Ch. 3.8 - a Use Newtons method with x1=1 to find the root of...Ch. 3.8 - Explain why Newtons method fails when applied to...Ch. 3.8 - If f(x){xifx0xifx0 then the root of the equation....Ch. 3.8 - a Use Newtons method to find the critical numbers...Ch. 3.8 - Use Newtons method to find the absolute maximum...Ch. 3.8 - Use Newtons method to find the coordinates of the...Ch. 3.8 - Of the infinitely many fines that are tangent to...Ch. 3.8 - Use Newtons method to find the coordinates,...Ch. 3.8 - In the figure, the length of the chord AB is 4 cm...Ch. 3.8 - A car dealer sells a new car for 18,000. He also...Ch. 3.8 - The figure shows the sun located at the origin and...Ch. 3.9 - Find the most general antiderivative of the...Ch. 3.9 - Find the most general antiderivative of the...Ch. 3.9 - Find the most general antiderivative of the...Ch. 3.9 - Find the most general antiderivative of the...Ch. 3.9 - Find the most general antiderivative of the...Ch. 3.9 - Find the most general antiderivative of the...Ch. 3.9 - Find the most general antiderivative of the...Ch. 3.9 - Find the most general antiderivative of the...Ch. 3.9 - Find the most general antiderivative of the...Ch. 3.9 - Find the most general antiderivative of the...Ch. 3.9 - Find the most general antiderivative of the...Ch. 3.9 - Find the most general antiderivative of the...Ch. 3.9 - Find the most general antiderivative of the...Ch. 3.9 - Find the most general antiderivative of the...Ch. 3.9 - Find the most general antiderivative of the...Ch. 3.9 - Find the most general antiderivative of the...Ch. 3.9 - Find the most general antiderivative of the...Ch. 3.9 - Find the most general antiderivative of the...Ch. 3.9 - Find the most general antiderivative of the...Ch. 3.9 - Find the most general antiderivative of the...Ch. 3.9 - 21-22 Find the antiderivative F of f that...Ch. 3.9 - 21-22 Find the antiderivative F of f that...Ch. 3.9 - 23-42 Find f. f(x)=20x312x2+6xCh. 3.9 - 23-42 Find f. f(x)=x64x4+x+1Ch. 3.9 - 23-42 Find f. f(x)=4x3Ch. 3.9 - 23-42 Find f. f(x)=x2/3+x2/3Ch. 3.9 - 23-42 Find f. f(t)=12+sintCh. 3.9 - 23-42 Find f. f(t)=t2costCh. 3.9 - 23-42 Find f. f(x)=1+3x,f(4)=25Ch. 3.9 - 23-42 Find f. f(x)=5x43x2+4,f(1)=2Ch. 3.9 - 23-42 Find f. f(x)=x(6+5x),f(1)=10Ch. 3.9 - 23-42 Find f. f(t)=t+1/t3,t0,f(1)=6Ch. 3.9 - 23-42 Find f. f(t)=sect(sect+tant),/2t/2,f(/4)=1Ch. 3.9 - 23-42 Find f. f(x)=(x+1)/x,f(1)=5Ch. 3.9 - 23-42 Find f. f(x)=2+12x+12x2,f(0)=4,f(0)=12Ch. 3.9 - 23-42 Find f. f(x)=8x3+5,f(1)=0,f(1)=8Ch. 3.9 - 23-42 Find f. f()=sin+cos,f(0)=3,f(0)=4Ch. 3.9 - 23-42 Find f. f(t)=46/t4,f(1)=6,f(2)=9,t0Ch. 3.9 - 23-42 Find f. f(x)=4+6x+24x2,f(0)=3,f(1)=10Ch. 3.9 - 23-42 Find f. f(x)=20x3+12x2+4,f(0)=8,f(1)=5Ch. 3.9 - 23-42 Find f. f(t)=t3cost,f(0)=2,f(1)=2Ch. 3.9 - 23-42 Find f. f(x)=cosx,f(0)=1,f(0)=2,f(0)=3Ch. 3.9 - Given that the graph of f passes through the point...Ch. 3.9 - Find a function f such that f(x)=x3 and the line...Ch. 3.9 - 45-46 The graph of a function f is shown. Which...Ch. 3.9 - 45-46 The graph of a function f is shown. Which...Ch. 3.9 - The graph of a function is shown in the figure....Ch. 3.9 - The graph of the velocity function of a particle...Ch. 3.9 - The graph of f is shown in the figure. Sketch the...Ch. 3.9 - a Use a graphing device to graph f(x)=2x3x. b...Ch. 3.9 - 51-52 Draw a graph of f and use it to make a rough...Ch. 3.9 - 51-52 Draw a graph of f and use it to make a rough...Ch. 3.9 - 53-58 A particle is moving with the given data....Ch. 3.9 - 53-58 A particle is moving with the given data....Ch. 3.9 - 53-58 A particle is moving with the given data....Ch. 3.9 - 53-58 A particle is moving with the given data....Ch. 3.9 - 53-58 A particle is moving with the given data....Ch. 3.9 - 53-58 A particle is moving with the given data....Ch. 3.9 - A stone is dropped from the upper observation deck...Ch. 3.9 - Show that for motion in a straight line with...Ch. 3.9 - An object is projected upward with initial...Ch. 3.9 - Two balls are thrown upward from the edge of the...Ch. 3.9 - A stone was dropped off a cliff and hit the ground...Ch. 3.9 - If a diver of mass m stands at the end of a diving...Ch. 3.9 - A company estimates that the marginal cost in...Ch. 3.9 - The linear density of a rod of length 1 m is given...Ch. 3.9 - Since raindrops grow as they fall, their surface...Ch. 3.9 - A car is traveling at 50 mi/h when the brakes are...Ch. 3.9 - What constant acceleration is required to increase...Ch. 3.9 - A car braked with a constant deceleration of 16...Ch. 3.9 - A car is traveling at 100 km/h when the driver...Ch. 3.9 - A model rocket is fired vertically upward from...Ch. 3.9 - A high-speed bullet train accelerates and...Ch. 3.R - Explain the difference between an absolute maximum...Ch. 3.R - What does the Extreme Value Theorem say?Ch. 3.R - a State Fermats Theorem. b Define a critical...Ch. 3.R - Explain how the Closed Interval Method works.Ch. 3.R - a State Rolles Theorem. b State the Mean Value...Ch. 3.R - a State the Increasing/Decreasing Test. b What...Ch. 3.R - a State the First Derivative Test. b State the...Ch. 3.R - Explain the meaning of each of the following...Ch. 3.R - If you have a graphing calculator or computer, why...Ch. 3.R - a Given an initial approximation x1 to a root of...Ch. 3.R - a What is an antiderivative of a function f? b...Ch. 3.R - Determine whether the statement is true or false....Ch. 3.R - Determine whether the statement is true or false....Ch. 3.R - Determine whether the statement is true or false....Ch. 3.R - Determine whether the statement is true or false....Ch. 3.R - Determine whether the statement is true or false....Ch. 3.R - Determine whether the statement is true or false....Ch. 3.R - Determine whether the statement is true or false....Ch. 3.R - Determine whether the statement is true or false....Ch. 3.R - Determine whether the statement is true or false....Ch. 3.R - Determine whether the statement is true or false....Ch. 3.R - Determine whether the statement is true or false....Ch. 3.R - Determine whether the statement is true or false....Ch. 3.R - Determine whether the statement is true or false....Ch. 3.R - Determine whether the statement is true or false....Ch. 3.R - Determine whether the statement is true or false....Ch. 3.R - Determine whether the statement is true or false....Ch. 3.R - Determine whether the statement is true or false....Ch. 3.R - Determine whether the statement is true or false....Ch. 3.R - Determine whether the statement is true or false....Ch. 3.R - 1-6 Find the local and absolute extreme values of...Ch. 3.R - 1-6 Find the local and absolute extreme values of...Ch. 3.R - 1-6 Find the local and absolute extreme values of...Ch. 3.R - 1-6 Find the local and absolute extreme values of...Ch. 3.R - 1-6 Find the local and absolute extreme values of...Ch. 3.R - 1-6 Find the local and absolute extreme values of...Ch. 3.R - 7-12 Find the limit. limx3x4+x56x42x2+1Ch. 3.R - 7-12 Find the limit. limtt3t+2(2t1)(t2+t+1)Ch. 3.R - 7-12 Find the limit. limx4x2+13x1Ch. 3.R - 7-12 Find the limit. limx(x2+x3)Ch. 3.R - 7-12 Find the limit. limx(4x2+3x2x)Ch. 3.R - 7-12 Find the limit. limxsin4xxCh. 3.R - 13-15 Sketch the graph of a function that...Ch. 3.R - 13-15 Sketch the graph of a function that...Ch. 3.R - 13-15 Sketch the graph of a function that...Ch. 3.R - The figure shows the graph of the derivative f of...Ch. 3.R - 17-28 Use the guidelines of Section 3.5 to sketch...Ch. 3.R - 17-28 Use the guidelines of Section 3.5 to sketch...Ch. 3.R - 17-28 Use the guidelines of Section 3.5 to sketch...Ch. 3.R - 17-28 Use the guidelines of Section 3.5 to sketch...Ch. 3.R - 17-28 Use the guidelines of Section 3.5 to sketch...Ch. 3.R - 17-28 Use the guidelines of Section 3.5 to sketch...Ch. 3.R - 17-28 Use the guidelines of Section 3.5 to sketch...Ch. 3.R - 17-28 Use the guidelines of Section 3.5 to sketch...Ch. 3.R - 17-28 Use the guidelines of Section 3.5 to sketch...Ch. 3.R - 17-28 Use the guidelines of Section 3.5 to sketch...Ch. 3.R - 17-28 Use the guidelines of Section 3.5 to sketch...Ch. 3.R - 17-28 Use the guidelines of Section 3.5 to sketch...Ch. 3.R - 29-32 Produce graphs of f that reveal all the...Ch. 3.R - 29-32 Produce graphs of f that reveal all the...Ch. 3.R - 29-32 Produce graphs of f that reveal all the...Ch. 3.R - 29-32 Produce graphs of f that reveal all the...Ch. 3.R - Show that the equation 3x+2cosx+5=0 has exactly...Ch. 3.R - Suppose that f is continuous on 0, 4, f(0)=1, and...Ch. 3.R - By applying the Mean Value Theorem to the function...Ch. 3.R - For what values of the constants a and b is 1, 3 a...Ch. 3.R - Let g(x)=f(x2), where f is twice differentiable...Ch. 3.R - Find two positive integers such that the sum of...Ch. 3.R - Show that the shortest distance from the point...Ch. 3.R - Find the point on the hyperbola xy=8 that is...Ch. 3.R - Find the smallest possible area of an isosceles...Ch. 3.R - Find the volume of the largest circular cone that...Ch. 3.R - In ABC,D lies on AB,CDAB,|AD|=|BD|=4cm, and...Ch. 3.R - Solve Exercise 43 when |CD|=2cm. In ABC,D lies on...Ch. 3.R - The velocity of a wave of length L in deep water...Ch. 3.R - A metal storage tank with volume V is to be...Ch. 3.R - A hockey team plays in an arena with a seating...Ch. 3.R - A manufacturer determines that the cost of making...Ch. 3.R - Use Newtons method to find the root of the...Ch. 3.R - Use Newtons method to find all solutions of the...Ch. 3.R - Use Newtons method to find the absolute maximum...Ch. 3.R - Use the guidelines in Section 3.5 to sketch the...Ch. 3.R - 53-54 Find the most general antiderivative of the...Ch. 3.R - 53-54 Find the most general antiderivative of the...Ch. 3.R - 55-58 Find f. f(t)=2t3sint,f(0)=5Ch. 3.R - 55-58 Find f. f(u)=u2+uu,f(1)=3Ch. 3.R - 55-58 Find f. f(x)=16x+48x2,f(0)=1,f(0)=2Ch. 3.R - 55-58 Find f. f(x)=5x3+6x2+2,f(0)=3,f(1)=2Ch. 3.R - A particle is moving according to the given data....Ch. 3.R - A particle is moving according to the given data....Ch. 3.R - Use a graphing device to draw a graph of the...Ch. 3.R - Investigate the family of curves given by...Ch. 3.R - A canister is dropped from a helicopter 500 m...Ch. 3.R - In an automobile race along a straight road, car A...Ch. 3.R - A rectangular beam will be cut from a cylindrical...Ch. 3.R - If a projectile is fired with an initial velocity...Ch. 3.R - A light is to be placed atop a pole of height h...Ch. 3.R - If f(x)=cos2xx2+x+1,x, use the graphs of f, f and...Ch. 3.P - Show that |sinxcosx|2 for all xCh. 3.P - Show that x2y2(4x2)(4y)216 for all numbers x and y...Ch. 3.P - Show that the inflection points of the curve...Ch. 3.P - Find the point on the parabola y=1x2 at which the...Ch. 3.P - Find the highest and lowest points on the curve...Ch. 3.P - Water is flowing at a constant rate into a...Ch. 3.P - Find the absolute maximum value of the function...Ch. 3.P - Find a function f such that f(1)=12,f(0)=0, and...Ch. 3.P - If P(a,a2) is any point on the parabola y=x2,...Ch. 3.P - An isosceles triangle is circumscribed about the...Ch. 3.P - The line y=mx+b intersects the parabola y=x2 in...Ch. 3.P - Sketch the graph of a function f such that f(x)0...Ch. 3.P - Determine the values of the number a for which the...Ch. 3.P - Sketch the region in the place consisting of all...Ch. 3.P - Let ABC be a triangle with BAC=120 and |AB||AC|=1...Ch. 3.P - a Let ABC be a triangle with right angle A and...Ch. 3.P - A triangle with sides a, b, and c varies with time...Ch. 3.P - ABCD is a square piece of paper with sides of...Ch. 3.P - The speeds of sound c1 in an upper layer and c2 in...Ch. 3.P - For what values of c is there is a straight line...Ch. 3.P - One of the problems posed by the Marquis de...Ch. 3.P - Given a sphere with radius r, find the height of a...Ch. 3.P - Assume that a snowball melts so that its volume...Ch. 3.P - A hemispherical bubble is placed on a spherical...

Additional Math Textbook Solutions

Find more solutions based on key concepts
Rewrite each expression in Exercises 116 as a single rational expression, simplified as much as possible. xx313...

Finite Mathematics and Applied Calculus (MindTap Course List)

Use the Intermediate Value Theorem to show that there is a root of the given equation in the specified interval...

Calculus: Early Transcendentals

Boyles Law states that when a sample of gas is compressed al a constant temperature, the product of the pressur...

Single Variable Calculus: Early Transcendentals, Volume I

Using Properties of Limits In Exercises 25-36, find the limit using direct substitution. See Examples 3 and 4. ...

Calculus: An Applied Approach (MindTap Course List)

Sketch the solid consisting of all points with spherical coordinates (, , ) such that 0 /2, 0 /6 and 0 ...

Multivariable Calculus

Describe the set of points (x,y) such that x2+y2=9.

Applied Calculus

Real and Imaginary Parts Find the real and imaginary parts of the complex number. 15. 3+4

Precalculus: Mathematics for Calculus (Standalone Book)

Sketching Transformations Use the graph of f shown in the figure to sketch the graph of" each function. To prin...

Calculus: Early Transcendental Functions

Recent research suggests that the amount of lime that parents spend talking about numbers can have a big impact...

Essentials of Statistics for The Behavioral Sciences (MindTap Course List)

SOC Data on several variables measuring overall health and well-being for 11 nations are reported here for 2010...

Essentials Of Statistics

Use a stem and leaf display to organize the following distribution of scores. Use six stems with each stem corr...

Statistics for The Behavioral Sciences (MindTap Course List)

Find an expression for the function whose graph is the given curve. 52. The line segment joining the points (5,...

Single Variable Calculus

In Exercises 39-50, sketch the graph of the function with the given rule. Find the domain and range of the func...

Applied Calculus for the Managerial, Life, and Social Sciences: A Brief Approach

Critical Thinking Sam computed a 95% confidence interval for from a specific random sample. His confidence int...

Understanding Basic Statistics

New Users The number of registered users at OHaganBooks.com has increased substantially over the past few month...

Finite Mathematics

In Problems 7-13, use derivative formulas to find the derivative of each function. Simplify, except for Problem...

Mathematical Applications for the Management, Life, and Social Sciences

For Problems 79-99, answer the question with an algebraic expression. Objective 3 Tina has c cents, which is al...

Intermediate Algebra

In Exercises 45 to 48, draw Venn diagrams to determine whether the expressions arc equal for all sets A, B, and...

Mathematical Excursions (MindTap Course List)

A pipe is 72 in. long. Cut three pieces of the following lengths from the pipe: 1634in.,2478in.,and12516in. Ass...

Elementary Technical Mathematics

Suppose that the base of the square pyramid in Exercise 5 has an area of 16cm2 and that the altitude of the pyr...

Elementary Geometry For College Students, 7e

Sales delay is the elapsed time between the manufacture of a product and its sale. According to the article War...

Probability and Statistics for Engineering and the Sciences

Finding a Limit In Exercises 5-22, find the limit. limx73xx+2

Calculus of a Single Variable

Let u=1+x33!+x66!+x99!+v=x+x44!+x77!+x1010!+w=x22!+x55!+x88!+ Show that u3 + v3 + w3 3uvw = 1.

Single Variable Calculus: Early Transcendentals

22. Let be a ring with finite number of elements. Show that the characteristic of divides .

Elements Of Modern Algebra

Find sin,cos, and tan for each value of . (Do not use calculators.) 90

Trigonometry (MindTap Course List)

Heather Gott bought a home with an adjustable-rate mortgage. The lenders margin on the loan is 3.5, and the ove...

Contemporary Mathematics for Business & Consumers

True or False: The domain is all numbers x for which f(x) is defined.

Study Guide for Stewart's Single Variable Calculus: Early Transcendentals, 8th

The directrix of the conic given by is:

Study Guide for Stewart's Multivariable Calculus, 8th

HOW DO YOU SEE IT? The graph shows the probability density function for a car brandthat has a mean fuel efficie...

Calculus: Early Transcendental Functions (MindTap Course List)

In Exercises 33 to 36, find the value of the indicated variable for each given formula. Y,ifm=YyXx,m=32,y=1,X=2...

Elementary Geometry for College Students

SELF-STORAGE UNITS LA Self Storage wishes to construct a facility comprising storage units of four different si...

Finite Mathematics for the Managerial, Life, and Social Sciences

Centripetal Force An object of mass m moves at a constant speed v in a circular path of radius v according to t...

Multivariable Calculus

Sketching a Surface in SpaceIn Exercises 4958, describe and sketch the surface. y=cosz

Calculus

Spherical-to-Rectangular ConversionIn Exercises 5158, find an equation in rectangular coordinates for the surfa...

Calculus (MindTap Course List)

A sample containing years to maturity and yield (%) for 40 corporate bonds is contained in the data file named ...

STATISTICS F/BUSINESS+ECONOMICS-TEXT

Identify the statistical techniques that are appropriate for each nonexperimental, quasi-experimental, and deve...

Research Methods for the Behavioral Sciences (MindTap Course List)

Simple random sampling was used to obtain a sample of n = 100 elements from a population of N = 1000. The sampl...

Statistics for Business & Economics, Revised (MindTap Course List)

Perform the operations and simplify. z+4z-6

College Algebra (MindTap Course List)

Express each area as indicated. Round each answer to the same number of significant digits as in the original q...

Mathematics For Machine Technology

Under what circumstances is a stratified random sample preferred to a simple random sample?

Research Methods for the Behavioral Sciences (MindTap Course List)

A box contains five slips of paper, marked 1, 1, 1, 10, and 25. The winner of a contest selects two slips of pa...

Introduction To Statistics And Data Analysis

Tablet PC Comparison provides a wide variety of information about tablet computers. The company’s website enabl...

Essentials Of Statistics For Business & Economics

In Exercises 31-38, do the following. a. Perform the given computation, working solely in the given base. b. Ch...

Mathematics: A Practical Odyssey

Motherboards A manufacturer produces motherboards and chips for computers. The production line produces 45 item...

Functions and Change: A Modeling Approach to College Algebra (MindTap Course List)

Use a diagram to shoe that the following argument can have true premise and a false conclusion. All dogs are ca...

Discrete Mathematics With Applications

For the following exercises, write the equation in equivalent exponential form. 246. log381=4

Calculus Volume 1

The following table reports the percentage of stocks in a portfolio for nine quarters from 2011 to 2013. Const...

Modern Business Statistics with Microsoft Office Excel (with XLSTAT Education Edition Printed Access Card) (MindTap Course List)

In Problems 39-44 proceed as in Examples 7 and 8 to find a solution of the given boundary-value problem. 44. x2...

A First Course in Differential Equations with Modeling Applications (MindTap Course List)

The golf scores for a school team were normally distributed with a mean of 68 and a standard deviation of three...

Introductory Statistics

Chemistry Thirty liters of a 40% acid solution is obtained by mixing a 25% solution with a 50% solution. (a) Wr...

College Algebra

bartleby
  • Contact Research (Essays)
  • High School Textbooks
  • Literature Guides
  • Essay Help
  • Mobile App
    • © 2021 bartleby. All Rights Reserved.