
Concept explainers
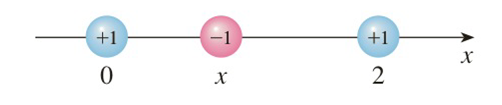
Coulomb’s Law states that the force of attraction between two charged particles is directly proportional to the product of the charges and inversely proportional to the square of the distance between them. The figure shows particles with charge 1 located at positions 0 and 2 on a coordinate line and a particle with charge
where
Want to see the full answer?
Check out a sample textbook solution
Chapter 3 Solutions
Calculus (MindTap Course List)
- Find the constant of proportionality. z is directly proportional to the sum of x and y. If x=2 and y=5, then z=28.arrow_forwardHookes Law Hookes Law states that the force needed to keep a spring stretched x units beyond its natural length is directly proportional to x. Here the constant of proportionality is called the spring constant. a Write Hookes Law as an equation. b If a spring has a natural length of 5 cm and a force of 30 N is required to maintain the spring stretched to a length of 9 cm, find the spring constant. c What force is needed to keep the spring stretched to a length of 11 cm?arrow_forwardFind the constant of proportionality. y is directly proportional to x. If x=30, then y=15.arrow_forward
- Algebra & Trigonometry with Analytic GeometryAlgebraISBN:9781133382119Author:SwokowskiPublisher:Cengage
 College AlgebraAlgebraISBN:9781305115545Author:James Stewart, Lothar Redlin, Saleem WatsonPublisher:Cengage Learning
College AlgebraAlgebraISBN:9781305115545Author:James Stewart, Lothar Redlin, Saleem WatsonPublisher:Cengage Learning Functions and Change: A Modeling Approach to Coll...AlgebraISBN:9781337111348Author:Bruce Crauder, Benny Evans, Alan NoellPublisher:Cengage Learning
Functions and Change: A Modeling Approach to Coll...AlgebraISBN:9781337111348Author:Bruce Crauder, Benny Evans, Alan NoellPublisher:Cengage Learning  Algebra and Trigonometry (MindTap Course List)AlgebraISBN:9781305071742Author:James Stewart, Lothar Redlin, Saleem WatsonPublisher:Cengage Learning
Algebra and Trigonometry (MindTap Course List)AlgebraISBN:9781305071742Author:James Stewart, Lothar Redlin, Saleem WatsonPublisher:Cengage Learning
 College Algebra (MindTap Course List)AlgebraISBN:9781305652231Author:R. David Gustafson, Jeff HughesPublisher:Cengage Learning
College Algebra (MindTap Course List)AlgebraISBN:9781305652231Author:R. David Gustafson, Jeff HughesPublisher:Cengage Learning





