Math
CalculusCalculus: An Applied Approach (MindTap Course List)Approximating the Area of a Plane Region In Exercises 1-6, use the rectangles to approximate the area of the region. Compare your result with the exact area obtained using a definite integral. See Example 1. f ( x ) = − x + 3 , [ 1 , 3 ]Approximating the Area of a Plane Region In Exercises 1-6, use the rectangles to approximate the area of the region. Compare your result with the exact area obtained using a definite integral. See Example 1. f ( x ) = − x + 3 , [ 1 , 3 ]
BuyFindlaunch
Calculus: An Applied Approach (Min...
10th Edition
Ron Larson
Publisher: Cengage Learning
ISBN: 9781305860919
BuyFindlaunch
Calculus: An Applied Approach (Min...
10th Edition
Ron Larson
Publisher: Cengage Learning
ISBN: 9781305860919
Solutions
Chapter
Section
Chapter 5.6, Problem 1E
Textbook Problem
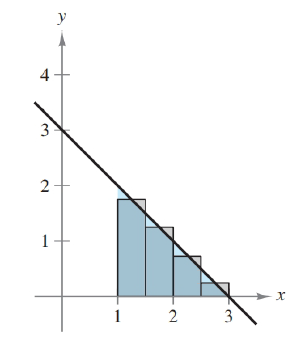
Approximating the Area of a Plane Region In Exercises 1-6, use the rectangles to approximate the area of the region. Compare your result with the exact area obtained using a definite integral. See Example 1.
check_circle
Expert Solution
Want to see the full answer?
Check out a sample textbook solution.Chapter 5 Solutions
Calculus: An Applied Approach (MindTap Course List)
Ch. 5.1 - Checkpoint 1 Worked-out solution available at...Ch. 5.1 - Checkpoint 2 Worked-out solution available at...Ch. 5.1 - Checkpoint 3 Worked-out solution available at...Ch. 5.1 - Checkpoint 4 Worked-out solution available at...Ch. 5.1 - Checkpoint 5 Worked-out solution available at...Ch. 5.1 - Checkpoint 6 Worked-out solution available at...Ch. 5.1 - Checkpoint 7 Worked-out solution available at...Ch. 5.1 - Checkpoint 8 Worked-out solution available at...Ch. 5.1 - In Exercises 1-6, rewrite the expression using...Ch. 5.1 - In Exercises 1-6, rewrite the expression using...
Ch. 5.1 - In Exercises 1-6, rewrite the expression using...Ch. 5.1 - In Exercises 1-6, rewrite the expression using...Ch. 5.1 - In Exercises 1-6, rewrite the expression using...Ch. 5.1 - In Exercises 1-6, rewrite the expression using...Ch. 5.1 - In Exercises 7-10, let (x, y) = (2, 2), and solve...Ch. 5.1 - In Exercises 7-10, let (x, y) = (2, 2), and solve...Ch. 5.1 - In Exercises 7-10, let (x, y) = (2, 2), and solve...Ch. 5.1 - In Exercises 7-10, let (x, y) = (2, 2), and solve...Ch. 5.1 - Integration and Differentiation In Exercises 1- 6,...Ch. 5.1 - Integration and Differentiation In Exercises 1- 6,...Ch. 5.1 - Integration and Differentiation In Exercises 1- 6,...Ch. 5.1 - Integration and Differentiation In Exercises 1- 6,...Ch. 5.1 - Integration and Differentiation In Exercises 1- 6,...Ch. 5.1 - Integration and Differentiation In Exercises 1-6,...Ch. 5.1 - Finding Indefinite Integrals In Exercises 7-18,...Ch. 5.1 - Finding Indefinite Integrals In Exercises 7-18,...Ch. 5.1 - Finding Indefinite Integrals In Exercises 7-18,...Ch. 5.1 - Finding Indefinite Integrals In Exercises 7-18,...Ch. 5.1 - Finding Indefinite Integrals In Exercises 7-18,...Ch. 5.1 - Finding Indefinite Integrals In Exercises 7-18,...Ch. 5.1 - Finding Indefinite Integrals In Exercises 7-18,...Ch. 5.1 - Finding Indefinite Integrals In Exercises 7-18,...Ch. 5.1 - Finding Indefinite Integrals In Exercises 7-18,...Ch. 5.1 - Finding Indefinite Integrals In Exercises 7-18,...Ch. 5.1 - Finding Indefinite Integrals In Exercises 7-18,...Ch. 5.1 - Finding Indefinite Integrals In Exercises 7-18,...Ch. 5.1 - Rewriting Before Integrating In Exercises 19-24,...Ch. 5.1 - Rewriting Before Integrating In Exercises 19-24,...Ch. 5.1 - Rewriting Before Integrating In Exercises 19-24,...Ch. 5.1 - Rewriting Before Integrating In Exercises 19-24,...Ch. 5.1 - Rewriting Before Integrating In Exercises 19-24,...Ch. 5.1 - Rewriting Before Integrating In Exercises 19-24,...Ch. 5.1 - Finding Indefinite Integrals In Exercises 25-36,...Ch. 5.1 - Finding Indefinite Integrals In Exercises 25-36,...Ch. 5.1 - Finding indefinite integrals In Exercises 2536,...Ch. 5.1 - Finding indefinite integrals In Exercises 2536,...Ch. 5.1 - Finding indefinite integrals In Exercises 2536,...Ch. 5.1 - Finding indefinite integrals In Exercises 2536,...Ch. 5.1 - Finding indefinite integrals In Exercises 2536,...Ch. 5.1 - Finding indefinite integrals In Exercises 2536,...Ch. 5.1 - Finding indefinite integrals In Exercises 2536,...Ch. 5.1 - Finding indefinite integrals In Exercises 2536,...Ch. 5.1 - Finding indefinite integrals In Exercises 2536,...Ch. 5.1 - Finding indefinite integrals In Exercises 2536,...Ch. 5.1 - Using Technology In Exercises 37 and 38, use a...Ch. 5.1 - Using Technology In Exercises 37 and 38, use a...Ch. 5.1 - Interpreting a Graph In Exercises 3942, the graph...Ch. 5.1 - Interpreting a Graph In Exercises 3942, the graph...Ch. 5.1 - Interpreting a Graph In Exercises 3942, the graph...Ch. 5.1 - Interpreting a Graph In Exercises 3942, the graph...Ch. 5.1 - Finding a Particular Solution In Exercises 4350,...Ch. 5.1 - Finding a Particular Solution In Exercises 4350,...Ch. 5.1 - Finding a Particular Solution In Exercises 4350,...Ch. 5.1 - Finding a Particular Solution In Exercises 4350,...Ch. 5.1 - Finding a Particular Solution In Exercises 4350,...Ch. 5.1 - Finding a Particular Solution In Exercises 4350,...Ch. 5.1 - Finding a Particular Solution In Exercises 4350,...Ch. 5.1 - Finding a Particular Solution In Exercises 4350,...Ch. 5.1 - Finding a Particular Solution In Exercises 5154,...Ch. 5.1 - Finding a Particular Solution In Exercises 5154,...Ch. 5.1 - Finding a Particular Solution In Exercises 5154,...Ch. 5.1 - Finding a Particular Solution In Exercises 5154,...Ch. 5.1 - Finding a Cost Function In Exercises 5558, find...Ch. 5.1 - Finding a Cost Function In Exercises 5558, find...Ch. 5.1 - Finding a Cost Function In Exercises 5558, find...Ch. 5.1 - Finding a Cost Function In Exercises 5558, find...Ch. 5.1 - Revenue and Demand In Exercises 59 and 60, find...Ch. 5.1 - Revenue and Demand In Exercises 59 and 60, find...Ch. 5.1 - Profit In Exercises 6164, find the profit function...Ch. 5.1 - Profit In Exercises 6164, find the profit function...Ch. 5.1 - Profit In Exercises 6164, find the profit function...Ch. 5.1 - Profit In Exercises 6164, find the profit function...Ch. 5.1 - Vertical Motion In Exercises 6568, use s(t)=32...Ch. 5.1 - Vertical Motion In Exercises 6568, use s(t)=32...Ch. 5.1 - Vertical Motion In Exercises 6568, use s(t) = 32...Ch. 5.1 - Vertical Motion In Exercises 6568, use s(t) = 32...Ch. 5.1 - Cost A company produces a product for which the...Ch. 5.1 - Gardening An evergreen nursery usually sells a...Ch. 5.1 - Population growth The growth rate of the...Ch. 5.1 - HOW DO YOU SEE IT? The graph shows the rate of...Ch. 5.1 - Vital Statistics The rate of increase of the...Ch. 5.1 - Internet Users The rate of growth of the number of...Ch. 5.1 - Economics: Marginal Benefits and Costs The table...Ch. 5.2 - Checkpoint 1 Worked-out solution available at...Ch. 5.2 - Checkpoint 2 Worked-out solution available at...Ch. 5.2 - Checkpoint 3 Worked-out solution available at...Ch. 5.2 - Checkpoint 4 Worked-out solution available at...Ch. 5.2 - Checkpoint 5 Worked-out solution available at...Ch. 5.2 - Checkpoint 6 Worked-out solution available at...Ch. 5.2 - Checkpoint 7 Worked-out solution available at...Ch. 5.2 - Checkpoint 8 Worked-out solution available at...Ch. 5.2 - In Exercises 1-9, find the indefinite integral....Ch. 5.2 - In Exercises 1-9, find the indefinite integral....Ch. 5.2 - In Exercises 1-9, find the indefinite integral....Ch. 5.2 - In Exercises 1-9, find the indefinite integral....Ch. 5.2 - In Exercises 1-9, find the indefinite integral....Ch. 5.2 - In Exercises 1-9, find the indefinite integral....Ch. 5.2 - In Exercises 1-9, find the indefinite integral....Ch. 5.2 - In Exercises 1-9, find the indefinite integral....Ch. 5.2 - In Exercises 1-9, find the indefinite integral....Ch. 5.2 - Finding u and du/dx In Exercises 1-8, identify u...Ch. 5.2 - Finding u and du/dx In Exercises 1-8, identify u...Ch. 5.2 - Finding u and du/dx In Exercises 1-8, identify u...Ch. 5.2 - Finding u and du/dx In Exercises 1-8, identify u...Ch. 5.2 - Finding u and du/dx In Exercises 1-8, identify u...Ch. 5.2 - Finding u and du/dx In Exercises 1-8, identify u...Ch. 5.2 - Finding u and du/dx In Exercises 1-8, identify u...Ch. 5.2 - Finding u and du/dx In Exercises 1-8, identify u...Ch. 5.2 - Applying the General Power Rule In Exercises 9-34,...Ch. 5.2 - Applying the General Power Rule In Exercises 9-34,...Ch. 5.2 - Applying the General Power Rule In Exercises 9-34,...Ch. 5.2 - Applying the General Power Rule In Exercises 9-34,...Ch. 5.2 - Applying the General Power Rule In Exercises 9-34,...Ch. 5.2 - Applying the General Power Rule In Exercises 9-34,...Ch. 5.2 - Applying the General Power Rule In Exercises 9-34,...Ch. 5.2 - Applying the General Power Rule In Exercises 9-34,...Ch. 5.2 - Applying the General Power Rule In Exercises 9-34,...Ch. 5.2 - Applying the General Power Rule In Exercises 9-34,...Ch. 5.2 - Applying the General Power Rule In Exercises 9-34,...Ch. 5.2 - Applying the General Power Rule In Exercises 9-34,...Ch. 5.2 - Applying the General Power Rule In Exercises 9-34,...Ch. 5.2 - Applying the General Power Rule In Exercises 9-34,...Ch. 5.2 - Applying the General Power Rule In Exercises 9-34,...Ch. 5.2 - Applying the General Power Rule In Exercises 9-34,...Ch. 5.2 - Applying the General Power Rule In Exercises 934,...Ch. 5.2 - Applying the General Power Rule In Exercises 934,...Ch. 5.2 - Applying the General Power Rule In Exercises 934,...Ch. 5.2 - Applying the General Power Rule In Exercises 934,...Ch. 5.2 - Applying the General Power Rule In Exercises 934,...Ch. 5.2 - Applying the General Power Rule In Exercises 934,...Ch. 5.2 - Applying the General Power Rule In Exercises 934,...Ch. 5.2 - Applying the General Power Rule In Exercises 934,...Ch. 5.2 - Applying the General Power Rule In Exercises 934,...Ch. 5.2 - Applying the General Power Rule In Exercises 934,...Ch. 5.2 - Integration by Substitution In Exercises 3542, use...Ch. 5.2 - Integration by Substitution In Exercises 3542, use...Ch. 5.2 - Integration by Substitution In Exercises 3542, use...Ch. 5.2 - Integration by Substitution In Exercises 3542, use...Ch. 5.2 - Integration by Substitution In Exercises 3542, use...Ch. 5.2 - Integration by Substitution In Exercises 3542, use...Ch. 5.2 - Integration by Substitution In Exercises 3542, use...Ch. 5.2 - Integration by Substitution In Exercises 3542, use...Ch. 5.2 - Comparing Methods In Exercises 43-46, (a) perform...Ch. 5.2 - Comparing Methods In Exercises 43-46, (a) perform...Ch. 5.2 - Comparing Methods In Exercises 43-46, (a) perform...Ch. 5.2 - Comparing Methods In Exercises 43-46, (a) perform...Ch. 5.2 - Finding an Equation of a Function In Exercises...Ch. 5.2 - Finding an Equation of a Function In Exercises...Ch. 5.2 - Finding an Equation of a Function In Exercises...Ch. 5.2 - Finding an Equation of a Function In Exercises...Ch. 5.2 - Cost The marginal cost of a product is modeled by...Ch. 5.2 - Cost The marginal cost of a product is modeled by...Ch. 5.2 - Supply In Exercises 53 and 54, find the supply...Ch. 5.2 - Supply In Exercises 53 and 54, find the supply...Ch. 5.2 - Supply In Exercises 53 and 54, find the supply...Ch. 5.2 - Supply In Exercises 53 and 54, find the supply...Ch. 5.2 - Gardening An evergreen nursery usually sells a...Ch. 5.2 - HOW DO YOU SEE IT? The graph shows the rate of...Ch. 5.2 - Marginal Propensity to Consume In Exercises 59 and...Ch. 5.2 - Marginal Propensity to Consume In Exercises 59 and...Ch. 5.2 - Integration Using Technology In Exercises 61 and...Ch. 5.2 - Integration Using Technology In Exercises 61 and...Ch. 5.3 - Checkpoint 1 Worked-out solution available at...Ch. 5.3 - Checkpoint 2 Worked out solution available at...Ch. 5.3 - Checkpoint 3 Worked-out solution available at...Ch. 5.3 - Checkpoint 4 Worked-out solution available at...Ch. 5.3 - Checkpoint 5 Worked-out solution available at...Ch. 5.3 - Checkpoint 6 Worked-out solution available at...Ch. 5.3 - Checkpoint 7 Worked-out solution available at...Ch. 5.3 - In Exercises 14, use long division to rewrite the...Ch. 5.3 - In Exercises 14, use long division to rewrite the...Ch. 5.3 - In Exercises 14, use long division to rewrite the...Ch. 5.3 - In Exercises 14, use long division to rewrite the...Ch. 5.3 - In Exercises 58, find the indefinite integral....Ch. 5.3 - In Exercises 58, find the indefinite integral....Ch. 5.3 - In Exercises 58, find the indefinite integral....Ch. 5.3 - In Exercises 58, find the indefinite integral....Ch. 5.3 - Integrating an Exponential Function In Exercises...Ch. 5.3 - Integrating an Exponential Function In Exercises...Ch. 5.3 - Integrating an Exponential Function In Exercises...Ch. 5.3 - Integrating an Exponential Function In Exercises...Ch. 5.3 - Integrating an Exponential Function In Exercises...Ch. 5.3 - Integrating an Exponential Function In Exercises...Ch. 5.3 - Integrating an Exponential Function In Exercises...Ch. 5.3 - Integrating an Exponential Function In Exercises...Ch. 5.3 - Integrating an Exponential Function In Exercises...Ch. 5.3 - Integrating an Exponential Function In Exercises...Ch. 5.3 - Integrating an Exponential Function In Exercises...Ch. 5.3 - Integrating an Exponential Function In Exercises...Ch. 5.3 - Using the log Rule for integration In Exercises...Ch. 5.3 - Using the log Rule for integration In Exercises...Ch. 5.3 - Using the log Rule for integration In Exercises...Ch. 5.3 - Using the log Rule for integration In Exercises...Ch. 5.3 - Using the log Rule for integration In Exercises...Ch. 5.3 - Using the log Rule for integration In Exercises...Ch. 5.3 - Using the log Rule for integration In Exercises...Ch. 5.3 - Using the log Rule for integration In Exercises...Ch. 5.3 - Using the log Rule for integration In Exercises...Ch. 5.3 - Using the log Rule for integration In Exercises...Ch. 5.3 - Using the log Rule for integration In Exercises...Ch. 5.3 - Using the log Rule for integration In Exercises...Ch. 5.3 - Using the log Rule for integration In Exercises...Ch. 5.3 - Using the log Rule for integration In Exercises...Ch. 5.3 - Using the log Rule for integration In Exercises...Ch. 5.3 - Using the log Rule for integration In Exercises...Ch. 5.3 - Using the log Rule for integration In Exercises...Ch. 5.3 - Using the log Rule for integration In Exercises...Ch. 5.3 - Finding indefinite integrals In Exercises 3146,...Ch. 5.3 - Finding indefinite integrals In Exercises 3146,...Ch. 5.3 - Finding indefinite integrals In Exercises 3146,...Ch. 5.3 - Finding indefinite integrals In Exercises 3146,...Ch. 5.3 - Finding indefinite integrals In Exercises 3146,...Ch. 5.3 - Finding indefinite integrals In Exercises 3146,...Ch. 5.3 - Finding indefinite integrals In Exercises 3146,...Ch. 5.3 - Finding indefinite integrals In Exercises 3146,...Ch. 5.3 - Finding indefinite integrals In Exercises 3146,...Ch. 5.3 - Finding indefinite integrals In Exercises 3146,...Ch. 5.3 - Finding indefinite integrals In Exercises 3146,...Ch. 5.3 - Finding indefinite integrals In Exercises 3146,...Ch. 5.3 - Finding indefinite integrals In Exercises 3146,...Ch. 5.3 - Finding indefinite integrals In Exercises 3146,...Ch. 5.3 - Finding indefinite integrals In Exercises 3146,...Ch. 5.3 - Finding indefinite integrals In Exercises 3146,...Ch. 5.3 - Finding an Equation of a Function In Exercises...Ch. 5.3 - Finding an Equation of a Function In Exercises...Ch. 5.3 - Finding an Equation of a Function In Exercises...Ch. 5.3 - Finding an Equation of a Function In Exercises...Ch. 5.3 - Biology A population P of bacteria is growing at...Ch. 5.3 - Biology Because of an insufficient oxygen supply,...Ch. 5.3 - Demand The marginal price for the demand of a...Ch. 5.3 - HOW DO YOU SEE IT? The graph shows the rate of...Ch. 5.3 - Revenue The rate of change in revenue for the...Ch. 5.3 - Revenue The rate of change in revenue for DIRECTV...Ch. 5.3 - True or False In Exercises 57 and 58, determine...Ch. 5.3 - True or False In Exercises 57 and 58, determine...Ch. 5.3 - In Exercises 1-9, find the indefinite integral....Ch. 5.3 - In Exercises 1-9, find the indefinite integral....Ch. 5.3 - In Exercises 1-9, find the indefinite integral....Ch. 5.3 - In Exercises 1-9, find the indefinite integral....Ch. 5.3 - In Exercises 1-9, find the indefinite integral....Ch. 5.3 - In Exercises 1-9, find the indefinite integral....Ch. 5.3 - In Exercises 1-9, find the indefinite integral....Ch. 5.3 - In Exercises 1-9, find the indefinite integral....Ch. 5.3 - In Exercises 1-9, find the indefinite integral....Ch. 5.3 - In Exercises 10 and 11, find the particular...Ch. 5.3 - In Exercises 10 and 11, find the particular...Ch. 5.3 - The marginal cost of producing x units of a...Ch. 5.3 - Find an equation of the function f whose graph...Ch. 5.3 - The number of bolts B produced by a foundry...Ch. 5.3 - In Exercises 1520, find the indefinite integral....Ch. 5.3 - In Exercises 1520, find the indefinite integral....Ch. 5.3 - In Exercises 1520, find the indefinite integral....Ch. 5.3 - In Exercises 1520, find the indefinite integral....Ch. 5.3 - In Exercises 1520, find the indefinite integral....Ch. 5.3 - In Exercises 1520, find the indefinite integral....Ch. 5.3 - The rate of change in revenue for Under Armour...Ch. 5.4 - Checkpoint 1 Worked-out solution available at...Ch. 5.4 - Checkpoint 2 Worked-out solution available at...Ch. 5.4 - Checkpoint 3 Worked-out solution available at...Ch. 5.4 - Checkpoint 4 Worked-out solution available at...Ch. 5.4 - Checkpoint 5 Worked-out solution available at...Ch. 5.4 - Checkpoint 6 Worked-out solution available at...Ch. 5.4 - Checkpoint 7 Worked-out solution available at...Ch. 5.4 - Checkpoint 8 Worked-out solution available at...Ch. 5.4 - Checkpoint 9 Worked-out solution available at...Ch. 5.4 - In Exercises 1-4, find the indefinite integral....Ch. 5.4 - In Exercises 1-4, find the indefinite integral....Ch. 5.4 - In Exercises 1-4, find the indefinite integral....Ch. 5.4 - In Exercises 1-4, find the indefinite integral....Ch. 5.4 - In Exercises 5-7, integrate the marginal function....Ch. 5.4 - In Exercises 5-7, integrate the marginal function....Ch. 5.4 - In Exercises 5-7, integrate the marginal function....Ch. 5.4 - Evaluating a Definite integral using a Geometric...Ch. 5.4 - Evaluating a Definite integral using a Geometric...Ch. 5.4 - Evaluating a Definite integral using a Geometric...Ch. 5.4 - Evaluating a Definite integral using a Geometric...Ch. 5.4 - Evaluating a Definite integral using a Geometric...Ch. 5.4 - Evaluating a Definite Integral Using a Geometric...Ch. 5.4 - Using Properties of Definite Integrals In...Ch. 5.4 - Using Properties of Definite Integrals In...Ch. 5.4 - Finding Area by the Fundamental Theorem In...Ch. 5.4 - Finding Area by the Fundamental Theorem In...Ch. 5.4 - Finding Area by the Fundamental Theorem In...Ch. 5.4 - Finding Area by the Fundamental Theorem In...Ch. 5.4 - Finding Area by the Fundamental Theorem In...Ch. 5.4 - Finding Area by the Fundamental Theorem In...Ch. 5.4 - Finding Area by the Fundamental Theorem In...Ch. 5.4 - Finding Area by the Fundamental Theorem In...Ch. 5.4 - Evaluating a Definite Integral In Exercises 17-38,...Ch. 5.4 - Evaluating a Definite Integral In Exercises 17-38,...Ch. 5.4 - Evaluating a Definite Integral In Exercises 17-38,...Ch. 5.4 - Evaluating a Definite Integral In Exercises 17-38,...Ch. 5.4 - Evaluating a Definite Integral In Exercises 17-38,...Ch. 5.4 - Evaluating a Definite Integral In Exercises 17-38,...Ch. 5.4 - Evaluating a Definite Integral In Exercises 17-38,...Ch. 5.4 - Evaluating a Definite Integral In Exercises 17-38,...Ch. 5.4 - Evaluating a Definite Integral In Exercises 17-38,...Ch. 5.4 - Evaluating a Definite Integral In Exercises 17-38,...Ch. 5.4 - Evaluating a Definite Integral In Exercises 17-38,...Ch. 5.4 - Evaluating a Definite Integral In Exercises 17-38,...Ch. 5.4 - Evaluating a Definite Integral In Exercises 17-38,...Ch. 5.4 - Evaluating a Definite Integral In Exercises 17-38,...Ch. 5.4 - Evaluating a Definite Integral In Exercises 17-38,...Ch. 5.4 - Evaluating a Definite Integral In Exercises 17-38,...Ch. 5.4 - Evaluating a Definite Integral In Exercises 17-38,...Ch. 5.4 - Evaluating a Definite Integral In Exercises 17-38,...Ch. 5.4 - Evaluating a Definite Integral In Exercises 1738,...Ch. 5.4 - Evaluating a Definite Integral In Exercises 1738,...Ch. 5.4 - Evaluating a Definite Integral In Exercises 1738,...Ch. 5.4 - Evaluating a Definite Integral In Exercises 1738,...Ch. 5.4 - Definite Integral Involving Absolute Value In...Ch. 5.4 - Definite Integral Involving Absolute Value In...Ch. 5.4 - Definite Integral Involving Absolute Value In...Ch. 5.4 - Definite Integral Involving Absolute Value In...Ch. 5.4 - Finding the Area of a Region In Exercises 43-46,...Ch. 5.4 - Finding the Area of a Region In Exercises 43-46,...Ch. 5.4 - Finding the Area of a Region In Exercises 43-46,...Ch. 5.4 - Finding the Area of a Region In Exercises 43-46,...Ch. 5.4 - Marginal Analysis In Exercises 4752, find the...Ch. 5.4 - Marginal Analysis In Exercises 4752, find the...Ch. 5.4 - Marginal Analysis In Exercises 4752, find the...Ch. 5.4 - Marginal Analysis In Exercises 4752, find the...Ch. 5.4 - Marginal Analysis In Exercises 4752, find the...Ch. 5.4 - Marginal Analysis In Exercises 4752, find the...Ch. 5.4 - Average Value of a Function In Exercises 53-60,...Ch. 5.4 - Average Value of a Function In Exercises 53-60,...Ch. 5.4 - Average Value of a Function In Exercises 53-60,...Ch. 5.4 - Average Value of a Function In Exercises 5360,...Ch. 5.4 - Average Value of a Function In Exercises 53-60,...Ch. 5.4 - Average Value of a Function In Exercises 53-60,...Ch. 5.4 - Average Value of a Function In Exercises 53-60,...Ch. 5.4 - Average Value of a Function In Exercises 53-60,...Ch. 5.4 - Integrating Even and Odd Functions In Exercises...Ch. 5.4 - Integrating Even and Odd Functions In Exercises...Ch. 5.4 - Integrating Even and Odd Functions In Exercises...Ch. 5.4 - Integrating Even and Odd Functions In Exercises...Ch. 5.4 - Using Properties of Definite Integrals Use the...Ch. 5.4 - Using Properties of Definite Integrals Use the...Ch. 5.4 - Finding the Amount of an Annuity In Exercises...Ch. 5.4 - Finding the Amount of an Annuity In Exercises...Ch. 5.4 - Finding the Amount of an Annuity In Exercises...Ch. 5.4 - Finding the Amount of an Annuity In Exercises...Ch. 5.4 - Capital Accumulation In Exercises 71-74, you are...Ch. 5.4 - Capital Accumulation In Exercises 71-74, you are...Ch. 5.4 - Capital Accumulation In Exercises 71-74, you are...Ch. 5.4 - Capital Accumulation In Exercises 71-74, you are...Ch. 5.4 - Cost The total cost of purchasing a piece of...Ch. 5.4 - Depreciation A company purchases a new machine for...Ch. 5.4 - Compound Interest A deposit of $2250 is made in a...Ch. 5.4 - HOW DO YOU SEE IT? A college graduate has two job...Ch. 5.4 - Mortgage Debt The rate of change of mortgage debt...Ch. 5.5 - Checkpoint 1 Worked-out solution available at...Ch. 5.5 - Checkpoint 2 Worked-out solution available at...Ch. 5.5 - Checkpoint 3 Worked-out solution available at...Ch. 5.5 - Checkpoint 4 Worked-out solution available at...Ch. 5.5 - Checkpoint 5 Worked-out solution available at...Ch. 5.5 - Checkpoint 6 Worked-out solution available at...Ch. 5.5 - In Exercises 1-4, simplify the expression....Ch. 5.5 - In Exercises 1-4, simplify the expression....Ch. 5.5 - In Exercises 1-4, simplify the expression....Ch. 5.5 - In Exercises 1-4, simplify the expression....Ch. 5.5 - In Exercises 5-8, find the points of intersection...Ch. 5.5 - In Exercises 5-8, find the points of intersection...Ch. 5.5 - In Exercises 5-8, find the points of intersection...Ch. 5.5 - In Exercises 5-8, find the points of intersection...Ch. 5.5 - Finding the Area Bounded by Two Graphs In...Ch. 5.5 - Finding the Area Bounded by Two Graphs In...Ch. 5.5 - Finding the Area Bounded by Two Graphs In...Ch. 5.5 - Finding the Area Bounded by Two Graphs In...Ch. 5.5 - Finding the Area Bounded by Two Graphs In...Ch. 5.5 - Finding the Area Bounded by Two Graphs In...Ch. 5.5 - Finding the Area Bounded by Two Graphs In...Ch. 5.5 - Finding the Area Bounded by Two Graphs In...Ch. 5.5 - Finding the Region In Exercises 9-12, the...Ch. 5.5 - Finding the Region In Exercises 9-12, the...Ch. 5.5 - Finding the Region In Exercises 9-12, the...Ch. 5.5 - Finding the Region In Exercises 9-12, the...Ch. 5.5 - Think About It In Exercises 13 and 14, determine...Ch. 5.5 - Think About It In Exercises 13 and 14, determine...Ch. 5.5 - Finding the Area Bounded by Two Graphs In...Ch. 5.5 - Finding the Area Bounded by Two Graphs In...Ch. 5.5 - Finding the Area Bounded by Two Graphs In...Ch. 5.5 - Finding the Area Bounded by Two Graphs In...Ch. 5.5 - Finding the Area Bounded by Two Graphs In...Ch. 5.5 - Finding the Area Bounded by Two Graphs In...Ch. 5.5 - Finding the Area Bounded by Two Graphs In...Ch. 5.5 - Finding the Area Bounded by Two Graphs In...Ch. 5.5 - Finding the Area Bounded by Two Graphs In...Ch. 5.5 - Finding the Area Bounded by Two Graphs In...Ch. 5.5 - Finding the Area Bounded by Two Graphs In...Ch. 5.5 - Finding the Area Bounded by Two Graphs In...Ch. 5.5 - Finding the Area Bounded by Two Graphs In...Ch. 5.5 - Finding the Area Bounded by Two Graphs In...Ch. 5.5 - Finding the Area Bounded by Two Graphs In...Ch. 5.5 - Finding the Area Bounded by Two Graphs In...Ch. 5.5 - Writing Integrals In Exercises 31-34, use a...Ch. 5.5 - Writing Integrals In Exercises 31-34, use a...Ch. 5.5 - Writing Integrals In Exercises 31-34, use a...Ch. 5.5 - Writing Integrals In Exercises 31-34, use a...Ch. 5.5 - Finding Area In Exercises 35-40, use a graphing...Ch. 5.5 - Finding Area In Exercises 35-40, use a graphing...Ch. 5.5 - Finding Area In Exercises 35-40, use a graphing...Ch. 5.5 - Finding Area In Exercises 35-40, use a graphing...Ch. 5.5 - Finding Area In Exercises 35-40, use a graphing...Ch. 5.5 - Finding Area In Exercises 35-40, use a graphing...Ch. 5.5 - Area of a Region In Exercises 41 and 42, use...Ch. 5.5 - Area of a Region In Exercises 41 and 42, use...Ch. 5.5 - Consumer and Producer Surpluses In Exercises...Ch. 5.5 - Consumer and Producer Surpluses In Exercises...Ch. 5.5 - Consumer and Producer Surpluses In Exercises...Ch. 5.5 - Consumer and Producer Surpluses In Exercises...Ch. 5.5 - Consumer and Producer Surpluses In Exercises...Ch. 5.5 - Consumer and Producer Surpluses In Exercises...Ch. 5.5 - Revenue In Exercises 49 and 50, two models, R1 and...Ch. 5.5 - Revenue In Exercises 49 and 50, two models, R1 and...Ch. 5.5 - Fuel Cost The projected fuel cost C (in millions...Ch. 5.5 - Health An epidemic was spreading such that t weeks...Ch. 5.5 - Consumer Trends For the years 2003 through 2012,...Ch. 5.5 - HOW DO YOU SEE IT? A state legislature is debating...Ch. 5.5 - Cost, Revenue, and Profit The revenue (in millions...Ch. 5.5 - Cost, Revenue, and Profit Repeat Exercise 55 for...Ch. 5.5 - Consumer and Producer Surpluses Factory orders for...Ch. 5.5 - Consumer and Producer Surpluses Repeat Exercise 57...Ch. 5.6 - Checkpoint 1 Worked-out solution available at...Ch. 5.6 - Checkpoint 2 Worked-out solution available at...Ch. 5.6 - Checkpoint 3 Worked-out solution available at...Ch. 5.6 - In Exercises 1-6, find the midpoint of the...Ch. 5.6 - In Exercises 1-6, find the midpoint of the...Ch. 5.6 - In Exercises 1-6, find the midpoint of the...Ch. 5.6 - In Exercises 1-6, find the midpoint of the...Ch. 5.6 - In Exercises 1-6, find the midpoint of the...Ch. 5.6 - In Exercises 1-6, find the midpoint of the...Ch. 5.6 - In Exercises 7-10, find the limit....Ch. 5.6 - In Exercises 7-10, find the limit. limx4x+57x5Ch. 5.6 - In Exercises 7-10, find the limit. limxx7x2+1Ch. 5.6 - In Exercises 7-10, find the limit....Ch. 5.6 - Approximating the Area of a Plane Region In...Ch. 5.6 - Approximating the Area of a Plane Region In...Ch. 5.6 - Approximating the Area of a Plane Region In...Ch. 5.6 - Approximating the Area of a Plane Region In...Ch. 5.6 - Approximating the Area of a Plane Region In...Ch. 5.6 - Approximating the Area of a Plane Region In...Ch. 5.6 - Using the Midpoint Rule In Exercises 7-14, use the...Ch. 5.6 - Using the Midpoint Rule In Exercises 7-14, use the...Ch. 5.6 - Using the Midpoint Rule In Exercises 7-14, use the...Ch. 5.6 - Using the Midpoint Rule In Exercises 7-14, use the...Ch. 5.6 - Using the Midpoint Rule In Exercises 7-14, use the...Ch. 5.6 - Using the Midpoint Rule In Exercises 7-14, use the...Ch. 5.6 - Using the Midpoint Rule In Exercises 7-14, use the...Ch. 5.6 - Using the Midpoint Rule In Exercises 7-14, use the...Ch. 5.6 - Using the Midpoint Rule In Exercises 15-20, use...Ch. 5.6 - Using the Midpoint Rule In Exercises 15-20, use...Ch. 5.6 - Using the Midpoint Rule In Exercises 15-20, use...Ch. 5.6 - Using the Midpoint Rule In Exercises 15-20, use...Ch. 5.6 - Using the Midpoint Rule In Exercises 15-20, use...Ch. 5.6 - Using the Midpoint Rule In Exercises 15-20, use...Ch. 5.6 - Surface Area Use the Midpoint Rule to estimate the...Ch. 5.6 - Surface Area Use the Midpoint Rule to estimate the...Ch. 5.6 - Surface Area Use the Midpoint Rule to estimate the...Ch. 5.6 - Numerical Approximation Use the Midpoint Rule with...Ch. 5 - Finding Indefinite Integrals In Exercises 114,...Ch. 5 - Finding Indefinite Integrals In Exercises 114,...Ch. 5 - Finding Indefinite Integrals In Exercises 114,...Ch. 5 - Finding Indefinite Integrals In Exercises 114,...Ch. 5 - Finding Indefinite Integrals In Exercises 114,...Ch. 5 - Finding Indefinite Integrals In Exercises 114,...Ch. 5 - Finding Indefinite Integrals In Exercises 114,...Ch. 5 - Finding Indefinite Integrals In Exercises 114,...Ch. 5 - Finding Indefinite Integrals In Exercises 114,...Ch. 5 - Finding Indefinite Integrals In Exercises 114,...Ch. 5 - Finding Indefinite Integrals In Exercises 114,...Ch. 5 - Finding Indefinite Integrals In Exercises 114,...Ch. 5 - Finding Indefinite Integrals In Exercises 114,...Ch. 5 - Finding Indefinite Integrals In Exercises 114,...Ch. 5 - Finding a Particular Solution In Exercises 1518,...Ch. 5 - Finding a Particular Solution In Exercises 1518,...Ch. 5 - Finding a Particular Solution In Exercises 1518,...Ch. 5 - Finding a Particular Solution In Exercises 1518,...Ch. 5 - Vertical Motion An object is projected upward from...Ch. 5 - Revenue A company produces a new product for which...Ch. 5 - Applying the General Power Rule In Exercises 2132,...Ch. 5 - Applying the General Power Rule In Exercises 2132,...Ch. 5 - Applying the General Power Rule In Exercises 2132,...Ch. 5 - Applying the General Power Rule In Exercises 2132,...Ch. 5 - Applying the General Power Rule In Exercises 2132,...Ch. 5 - Applying the General Power Rule In Exercises 2132,...Ch. 5 - Applying the General Power Rule In Exercises 2132,...Ch. 5 - Applying the General Power Rule In Exercises 2132,...Ch. 5 - Applying the General Power Rule In Exercises 2132,...Ch. 5 - Applying the General Power Rule In Exercises 2132,...Ch. 5 - Applying the General Power Rule In Exercises 2132,...Ch. 5 - Applying the General Power Rule In Exercises 2132,...Ch. 5 - Production The rate of change of the output of a...Ch. 5 - Cost The marginal cost for a catering service to...Ch. 5 - Using the Exponential and Log Rules In Exercises...Ch. 5 - Using the Exponential and Log Rules In Exercises...Ch. 5 - Using the Exponential and Log Rules In Exercises...Ch. 5 - Using the Exponential and Log Rules In Exercises...Ch. 5 - Using the Exponential and Log Rules In Exercises...Ch. 5 - Using the Exponential and Log Rules In Exercises...Ch. 5 - Using the Exponential and Log Rules In Exercises...Ch. 5 - Using the Exponential and Log Rules In Exercises...Ch. 5 - Using the Exponential and Log Rules In Exercises...Ch. 5 - Using the Exponential and Log Rules In Exercises...Ch. 5 - Using the Exponential and Log Rules In Exercises...Ch. 5 - Using the Exponential and Log Rules In Exercises...Ch. 5 - Evaluating a Definite Integral using a Geometric...Ch. 5 - Evaluating a Definite Integral using a Geometric...Ch. 5 - Evaluating a Definite Integral using a Geometric...Ch. 5 - Evaluating a Definite Integral using a Geometric...Ch. 5 - Using Properties of Definite integrals Given...Ch. 5 - Using Properties of Definite Integrals Given...Ch. 5 - Finding Area by the Fundamental Theorem In...Ch. 5 - Finding Area by the Fundamental Theorem In...Ch. 5 - Finding Area by the Fundamental Theorem In...Ch. 5 - Finding Area by the Fundamental Theorem In...Ch. 5 - Finding Area by the Fundamental Theorem In...Ch. 5 - Finding Area by the Fundamental Theorem In...Ch. 5 - Evaluating a Definite Integral In Exercises 5970,...Ch. 5 - Evaluating a Definite Integral In Exercises 5970,...Ch. 5 - Evaluating a Definite Integral In Exercises 5970,...Ch. 5 - Evaluating a Definite Integral In Exercises 5970,...Ch. 5 - Evaluating a Definite Integral In Exercises 5970,...Ch. 5 - Evaluating a Definite Integral In Exercises 5970,...Ch. 5 - Evaluating a Definite Integral In Exercises 5970,...Ch. 5 - Evaluating a Definite Integral In Exercises 5970,...Ch. 5 - Evaluating a Definite Integral In Exercises 5970,...Ch. 5 - Evaluating a Definite Integral In Exercises 5970,...Ch. 5 - Evaluating a Definite Integral In Exercises 5970,...Ch. 5 - Evaluating a Definite Integral In Exercises 5970,...Ch. 5 - Average Value of a Function In Exercises 7176,...Ch. 5 - Average Value of a Function In Exercises 7176,...Ch. 5 - Average Value of a Function In Exercises 71-76,...Ch. 5 - Average Value of a Function In Exercises 7176,...Ch. 5 - Average Value of a Function In Exercises 7176,...Ch. 5 - Average Value of a Function In Exercises 7176,...Ch. 5 - Integrating Even and Odd Functions In Exercises...Ch. 5 - Integrating Even and Odd Functions In Exercises...Ch. 5 - Integrating Even and Odd Functions In Exercises...Ch. 5 - Integrating Even and Odd Functions In Exercises...Ch. 5 - Finding the Amount of an Annuity In Exercises 81...Ch. 5 - Finding the Amount of an Annuity In Exercises 81...Ch. 5 - Cost The marginal cost of serving an additional...Ch. 5 - Profit The marginal profit obtained by selling x...Ch. 5 - Compound Interest A deposit of $500 is made in a...Ch. 5 - Sales The rate of change in sales for Garmin from...Ch. 5 - Finding the Area Bounded by Two Graphs In...Ch. 5 - Finding the Area Bounded by Two Graphs In...Ch. 5 - Finding the Area Bounded by Two Graphs In...Ch. 5 - Finding the Area Bounded by Two Graphs In...Ch. 5 - Finding the Area Bounded by Two Graphs In...Ch. 5 - Finding the Area Bounded by Two Graphs In...Ch. 5 - Finding the Area Bounded by Two Graphs In...Ch. 5 - Finding the Area Bounded by Two Graphs In...Ch. 5 - Consumer and Producer Surpluses In Exercises...Ch. 5 - Consumer and Producer Surpluses In Exercises...Ch. 5 - Consumer and Producer Surpluses In Exercises...Ch. 5 - Consumer and Producer Surpluses In Exercises...Ch. 5 - Revenue For the years 2020 through 2025, two...Ch. 5 - Revenue For the years 2004 through 2013, the...Ch. 5 - Cost, Revenue, and Profit The revenue (in millions...Ch. 5 - Cost, Revenue, and Profit Repeat Exercise 101 for...Ch. 5 - Approximating the Area of a Plane Region In...Ch. 5 - Approximating the Area of a Plane Region In...Ch. 5 - Using the Midpoint Rule In Exercises 105-110, use...Ch. 5 - Using the Midpoint Rule In Exercises 105-110, use...Ch. 5 - Using the Midpoint Rule In Exercises 105-110, use...Ch. 5 - Using the Midpoint Rule In Exercises 105-110, use...Ch. 5 - Using the Midpoint Rule In Exercises 105-110, use...Ch. 5 - Using the Midpoint Rule In Exercises 105-110, use...Ch. 5 - Using the Midpoint Rule In Exercises 111-114, use...Ch. 5 - Using the Midpoint Rule In Exercises 111-114, use...Ch. 5 - Using the Midpoint Rule In Exercises 111-114, use...Ch. 5 - Using the Midpoint Rule In Exercises 111-114, use...Ch. 5 - Surface Area Use the Midpoint Rule to estimate the...Ch. 5 - Take this test as you would take a test in class....Ch. 5 - Take this test as you would take a test in class....Ch. 5 - Take this test as you would take a test in class....Ch. 5 - Take this test as you would take a test in class....Ch. 5 - Take this test as you would take a test in class....Ch. 5 - Take this test as you would take a test in class....Ch. 5 - In Exercises 7 and 8, find the particular solution...Ch. 5 - In Exercises 7 and 8, find the particular solution...Ch. 5 - In Exercises 9-14, evaluate the definite integral....Ch. 5 - In Exercises 9-14, evaluate the definite integral....Ch. 5 - In Exercises 9-14, evaluate the definite integral....Ch. 5 - In Exercises 9-14, evaluate the definite integral....Ch. 5 - In Exercises 9-14, evaluate the definite integral....Ch. 5 - In Exercises 9-14, evaluate the definite integral....Ch. 5 - The rate of change in sales of Ross Stores from...Ch. 5 - In Exercises 16-19, sketch the region bounded by...Ch. 5 - In Exercises 16-19, sketch the region bounded by...Ch. 5 - In Exercises 16-19, sketch the region bounded by...Ch. 5 - In Exercises 16-19, sketch the region bounded by...Ch. 5 - The demand and supply functions for a product are...Ch. 5 - In Exercises 21 and 22, use the Midpoint Rule with...Ch. 5 - In Exercises 21 and 22, use the Midpoint Rule with...
Additional Math Textbook Solutions
Find more solutions based on key concepts
Production Costs Over at Duffin House, Marjory Duffin is trying to decide on the size of the print runs for the...
Finite Mathematics and Applied Calculus (MindTap Course List)
Simplify each expression in Exercises 1730, expressing your answer in positive exponent form. xy1x1
Applied Calculus
The second directional derivative of f(x, y) is Du2f(x, y) = Du[Du f(x, y)] If f(x, y) = x3 + 5x2y + y3 and u=3...
Calculus: Early Transcendentals
Find the Maclaurin series for f and its radius of convergence. You may use either the direct method (definition...
Multivariable Calculus
Exponents Simplify each expression, and eliminate any negative exponents. 41. (a) 8a3b42a5b5 (b) (y5x2)3
Precalculus: Mathematics for Calculus (Standalone Book)
Use the guidelines of this section to sketch the curve. y=1x+lnx
Single Variable Calculus: Early Transcendentals, Volume I
Sketching Transformations Consider the graph of the function f shown below. Use this graph to sketch the graphs...
Calculus: Early Transcendental Functions
SOC Are college students who live in dormitories significantly more involved in campus life than students who c...
Essentials Of Statistics
Find each or the followin.tt values for the distribution shown in the following polygon. a. n b. X c. X2
Essentials of Statistics for The Behavioral Sciences (MindTap Course List)
Hotel Occupancy Rate The occupancy rate of the all-suite Wonderland Hotel, located near a amusement park, is gi...
Applied Calculus for the Managerial, Life, and Social Sciences: A Brief Approach
Prove the statement using the , definition of a limit. 20. limx10(345x)=5
Single Variable Calculus
17 Find the cross product ab and verify that it is orthogonal to both a and b. a=2,3,0, b=1,0,5
Calculus (MindTap Course List)
For Problems 721, please provide the following information. (a) What is the level of significance? State the nu...
Understanding Basic Statistics
Complete the final! two columns in the following frequency distribution table and then find the percentiles and...
Statistics for The Behavioral Sciences (MindTap Course List)
In Problems 61-68, perform the indicated operations with expressions involving fractional exponents and radical...
Mathematical Applications for the Management, Life, and Social Sciences
In Exercises 47 to 54, find the number of subsets of the given set. {x | x is an odd integer between –4 and 8...
Mathematical Excursions (MindTap Course List)
A boiler has five identical relief valves. The probability that any particular valve will open on demand is .96...
Probability and Statistics for Engineering and the Sciences
For Problems 1-50, solve each equation. Objective 1 4x2x=5x+10
Intermediate Algebra
Find a formula for the described function and state its domain. 61. An open rectangular box with volume 2 m3 ha...
Single Variable Calculus: Early Transcendentals
In Exercises, use mathematical induction to prove that the given statement is true for all positive integers.
...
Elements Of Modern Algebra
Prove that each of the following identities is true. tancot=sin2cos2sincos
Trigonometry (MindTap Course List)
Prove that when the midpoints of consecutive sides of a quadrilateral are joined in order, the resulting quadri...
Elementary Geometry For College Students, 7e
Pamela Boyd borrowed $20,000 at 6.5% ordinary interest for 150 days. On day 30 of the loan, she made a partial ...
Contemporary Mathematics for Business & Consumers
Find the following information from Illustration 1: ILLUSTRATION 1 How many barrels per day were used by Italy?
Elementary Technical Mathematics
Removable and Nonremovable Discontinuities In Exercises 53-58, find the x-values (if any) at which f is not con...
Calculus: Early Transcendental Functions (MindTap Course List)
PUTNAM EXAM CHALLENGE From the vertex (0, c) of the catenary y=ccosh(x/c) a line L is drawn perpendicular to th...
Calculus of a Single Variable
In Exercises 1116, use the formula C(n,x)pxqnx to determine the probability of the given event. The probability...
Finite Mathematics for the Managerial, Life, and Social Sciences
In Exercises 5 to 10, classify each statement as simple, conditional, a conjunction, or a disjunction. If Alice...
Elementary Geometry for College Students
Finding Relative Extrema and Saddle Points Using Technology In Exercises 25-28, use a computer algebra system t...
Calculus (MindTap Course List)
MatchingIn Exercises 1922, match the equation with its graph. [The graphs are labeled (a), (b), (c), and (d).] ...
Multivariable Calculus
Finding Partial DerivativesIn Exercises 1926, find all finding partial derivatives. f(x,y)=xyx+y
Calculus
For what values of p does the series converge?
Study Guide for Stewart's Multivariable Calculus, 8th
From the Maclaurin series for ln(1 + x) and sin x, the first three terms of the Maclaurin series for (ln(1 + x)...
Study Guide for Stewart's Single Variable Calculus: Early Transcendentals, 8th
Nielsen Media Research identified American Idol and Dancing with the Stars as the two top-rated prime-time tele...
Statistics for Business & Economics, Revised (MindTap Course List)
What is the goal of a single-case experimental research design?
Research Methods for the Behavioral Sciences (MindTap Course List)
A zinc casting is in the shape of a frustum of a right circular cone. The larger base area is 280 inches in dia...
Mathematics For Machine Technology
Define plagiarism and explain the techniques that can be used to help avoid unintentional plagiarism.
Research Methods for the Behavioral Sciences (MindTap Course List)
Let fx=2x and gx=x. Find each value. gg81256
College Algebra (MindTap Course List)
Consumer Reports provides ratings for televisions, including energy cost per year (consumerreports.org/products...
Introduction To Statistics And Data Analysis
Given the ordered pairs (5,5), (7,10), (8,11), (10,15) and (13,16): a. Plot the ordered pairs. Do the ordered p...
Mathematics: A Practical Odyssey
Consider the following hypothesis test. H0: = 20 Ha: 20 A sample of 200 items will be taken and the populati...
STATISTICS F/BUSINESS+ECONOMICS-TEXT
Let a0,a1,a2,... be the sequence defined by the explicit formula an=c2+Dforeachintegern0, Where C and D are rea...
Discrete Mathematics With Applications
For the following exercises, for each linear equation, a. give the slope m and y -intercept b, if any, and b. g...
Calculus Volume 1
Use the following information to answer the next eleven exercises. The age of cars in the staff parking lot of ...
Introductory Statistics
Finding Equilibrium SolutionFind an equilibrium solution of dfdx=f(124f).
Functions and Change: A Modeling Approach to College Algebra (MindTap Course List)
In Problems 1524, x = 0 is a regular singular point of the given differential equation. Show that the indicial ...
A First Course in Differential Equations with Modeling Applications (MindTap Course List)
Consider the following time series data.
Construct a time series plot. What type of pattern exists in the data...
Modern Business Statistics with Microsoft Office Excel (with XLSTAT Education Edition Printed Access Card) (MindTap Course List)
In the following exercises, use a calculator to estimate the area under the curve by computing T10, the average...
Calculus Volume 2
Bullish, Neutral, or Bearish. The American Association of Individual Investors conducts a weekly survey of its ...
Essentials Of Statistics For Business & Economics
