
(a)
To find: The expression for a Riemann sum of a function
(a)
Answer to Problem 1RCC
The expression for a Riemann sum of a function f is
Explanation of Solution
The Riemann sum of a function f is the method to find the total area underneath a curve.
The area under the curve dividedas n number of approximating rectangles. Hence the Riemann sum of a function f is the sum of the area of the all individual rectangles.
Here,
Thus, the expression for a Riemann sum of a function f is
b)
To define: The geometric interpretation of a Riemann sum with diagram.
b)
Explanation of Solution
Given information:
Consider the condition for the function
The function
Sketch the curve
Show the curve as in Figure 1.
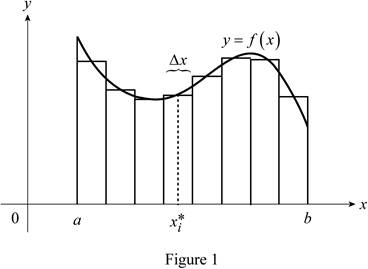
Refer to Figure 1
The function
Thus, the geometric interpretation of a Riemann sum of
c)
To define: The geometric interpretation of a Riemann sum, if the function
c)
Explanation of Solution
Given information:
The function
The function
Sketch the curve
Show the curve as in Figure 2.
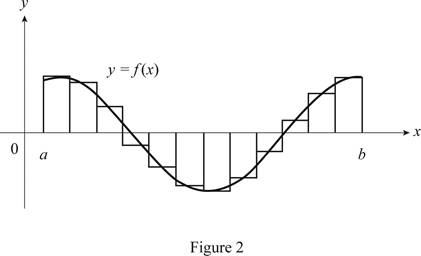
Refer figure 2,
The Riemann sum is the difference of areas of approximating rectangles above and below the x-axis
Therefore, the geometric interpretation of a Riemann sum is defined, if
Want to see more full solutions like this?
Chapter 5 Solutions
Single Variable Calculus: Concepts and Contexts, Enhanced Edition
 Calculus: Early TranscendentalsCalculusISBN:9781285741550Author:James StewartPublisher:Cengage Learning
Calculus: Early TranscendentalsCalculusISBN:9781285741550Author:James StewartPublisher:Cengage Learning Thomas' Calculus (14th Edition)CalculusISBN:9780134438986Author:Joel R. Hass, Christopher E. Heil, Maurice D. WeirPublisher:PEARSON
Thomas' Calculus (14th Edition)CalculusISBN:9780134438986Author:Joel R. Hass, Christopher E. Heil, Maurice D. WeirPublisher:PEARSON Calculus: Early Transcendentals (3rd Edition)CalculusISBN:9780134763644Author:William L. Briggs, Lyle Cochran, Bernard Gillett, Eric SchulzPublisher:PEARSON
Calculus: Early Transcendentals (3rd Edition)CalculusISBN:9780134763644Author:William L. Briggs, Lyle Cochran, Bernard Gillett, Eric SchulzPublisher:PEARSON Calculus: Early TranscendentalsCalculusISBN:9781319050740Author:Jon Rogawski, Colin Adams, Robert FranzosaPublisher:W. H. Freeman
Calculus: Early TranscendentalsCalculusISBN:9781319050740Author:Jon Rogawski, Colin Adams, Robert FranzosaPublisher:W. H. Freeman
 Calculus: Early Transcendental FunctionsCalculusISBN:9781337552516Author:Ron Larson, Bruce H. EdwardsPublisher:Cengage Learning
Calculus: Early Transcendental FunctionsCalculusISBN:9781337552516Author:Ron Larson, Bruce H. EdwardsPublisher:Cengage Learning





