
To Draw: the graph for the function
To Evaluate: The value of the integral function
Answer to Problem 38RE
The value of the integral function is 0.
Explanation of Solution
Given information:
The function is
The region lies between
Calculation:
Show the function as follows:
Substitute 0 for x in Equation (1).
Substitute
Calculate the remaining values of the function as shown below.
Show the x and
| x | |||
| 1.00 | 0.00 | 0.00 | |
| 0.75 | 0.50 | 0.38 | |
| 0.25 | 0.87 | 0.22 | |
| 0.00 | 1.00 | 0.00 | |
| 0.25 | 0.87 | 0.22 | |
| 0.75 | 0.50 | 0.38 | |
| 1.00 | 0.00 | 0.00 | |
| 0.75 | -0.50 | -0.38 | |
| 0.25 | -0.87 | -0.22 | |
| 0.00 | -1.00 | 0.00 | |
| 0.25 | -0.87 | -0.22 | |
| 0.75 | -0.50 | -0.38 | |
| 1.00 | 0.00 | 0.00 |
Table 1
Sketch the function as shown in Figure 1.
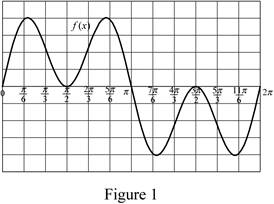
Refer to Figure 1.
The value of the integral function
Consider
Differentiate both sides of the Equation (2).
Calculate the lower limit value of u using Equation (2).
Substitute 0 for x in Equation (2).
Calculate the upper limit value of u using Equation (2).
Substitute
Substitute u for
Find the integral value of the function as shown below.
Therefore, the integral value of the function is 0.
Chapter 5 Solutions
Single Variable Calculus: Concepts and Contexts, Enhanced Edition
 Calculus: Early TranscendentalsCalculusISBN:9781285741550Author:James StewartPublisher:Cengage Learning
Calculus: Early TranscendentalsCalculusISBN:9781285741550Author:James StewartPublisher:Cengage Learning Thomas' Calculus (14th Edition)CalculusISBN:9780134438986Author:Joel R. Hass, Christopher E. Heil, Maurice D. WeirPublisher:PEARSON
Thomas' Calculus (14th Edition)CalculusISBN:9780134438986Author:Joel R. Hass, Christopher E. Heil, Maurice D. WeirPublisher:PEARSON Calculus: Early Transcendentals (3rd Edition)CalculusISBN:9780134763644Author:William L. Briggs, Lyle Cochran, Bernard Gillett, Eric SchulzPublisher:PEARSON
Calculus: Early Transcendentals (3rd Edition)CalculusISBN:9780134763644Author:William L. Briggs, Lyle Cochran, Bernard Gillett, Eric SchulzPublisher:PEARSON Calculus: Early TranscendentalsCalculusISBN:9781319050740Author:Jon Rogawski, Colin Adams, Robert FranzosaPublisher:W. H. Freeman
Calculus: Early TranscendentalsCalculusISBN:9781319050740Author:Jon Rogawski, Colin Adams, Robert FranzosaPublisher:W. H. Freeman
 Calculus: Early Transcendental FunctionsCalculusISBN:9781337552516Author:Ron Larson, Bruce H. EdwardsPublisher:Cengage Learning
Calculus: Early Transcendental FunctionsCalculusISBN:9781337552516Author:Ron Larson, Bruce H. EdwardsPublisher:Cengage Learning





