
(a)
To Analyze:
Whether the estimate is an underestimate or an overestimate using right endpoints.
(a)
Answer to Problem 4E
The estimate is an overestimate for the function
Explanation of Solution
Given information:
The curve function is
The region lies between
The number of rectangles
Draw the graph for the function
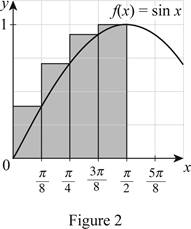
Draw four approximating rectangles using right end points for the function
The expression to find the lower estimate of areas of n rectangles
Here, the right endpoint height of the first rectangle is
Find the width
Here, the upper limit is b, the lower limit is a, and the number of rectangles is n.
Substitute
Refer Figure (2).
Take the right endpoint height of the first rectangle
Substitute 4 for n, 0.38for
Refer Figure (2).
The function curve as
Hence,
(b)
To Analyze:
Whether the estimate is an underestimate or an overestimate using right endpoints.
(b)
Answer to Problem 4E
The estimate is an underestimate for the function
Explanation of Solution
Draw four approximating rectangles using left end points for the function
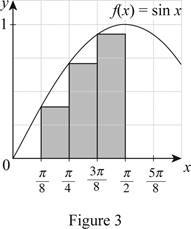
The expression to find the upper estimate of areas of 4 rectangles
Here, the lower estimate using right endpoints for
Refer Figure (3).
Take the left endpoint height of the uppermost left rectangle
Substitute 1.182 for
Refer Figure (3).
The function curve as
Hence,
Chapter 5 Solutions
Single Variable Calculus: Concepts and Contexts, Enhanced Edition
 Calculus: Early TranscendentalsCalculusISBN:9781285741550Author:James StewartPublisher:Cengage Learning
Calculus: Early TranscendentalsCalculusISBN:9781285741550Author:James StewartPublisher:Cengage Learning Thomas' Calculus (14th Edition)CalculusISBN:9780134438986Author:Joel R. Hass, Christopher E. Heil, Maurice D. WeirPublisher:PEARSON
Thomas' Calculus (14th Edition)CalculusISBN:9780134438986Author:Joel R. Hass, Christopher E. Heil, Maurice D. WeirPublisher:PEARSON Calculus: Early Transcendentals (3rd Edition)CalculusISBN:9780134763644Author:William L. Briggs, Lyle Cochran, Bernard Gillett, Eric SchulzPublisher:PEARSON
Calculus: Early Transcendentals (3rd Edition)CalculusISBN:9780134763644Author:William L. Briggs, Lyle Cochran, Bernard Gillett, Eric SchulzPublisher:PEARSON Calculus: Early TranscendentalsCalculusISBN:9781319050740Author:Jon Rogawski, Colin Adams, Robert FranzosaPublisher:W. H. Freeman
Calculus: Early TranscendentalsCalculusISBN:9781319050740Author:Jon Rogawski, Colin Adams, Robert FranzosaPublisher:W. H. Freeman
 Calculus: Early Transcendental FunctionsCalculusISBN:9781337552516Author:Ron Larson, Bruce H. EdwardsPublisher:Cengage Learning
Calculus: Early Transcendental FunctionsCalculusISBN:9781337552516Author:Ron Larson, Bruce H. EdwardsPublisher:Cengage Learning





