College Physics
11th Edition
ISBN: 9781305952300
Author: Raymond A. Serway, Chris Vuille
Publisher: Cengage Learning
expand_more
expand_more
format_list_bulleted
Concept explainers
Videos
Textbook Question
Chapter 7, Problem 74AP
A massless spring of constant k = 78.4 N/m is fixed on the left side of a level track. A block of mass m = 0.50 kg is pressed against the spring and compresses it a distance d, as in Figure P7.74. The block (initially at rest) is then released and travels toward a circular loop-the-loop of radius R = 1.5 m. The entire track and the loop-the-loop are frictionless, except for the section of track between points A and B. Given that the coefficient of kinetic friction between the block and the track along AB is μk = 0.30 and that the length of AB is 2.5 m, determine the minimum compression d of the spring that enables the block to just make it through the loop-the-loop at point C. Hint: The force exerted by the track on the block will be zero if the block barely makes it through the loop-the-loop.
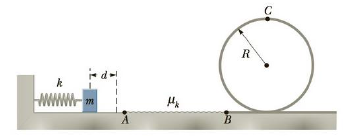
Figure P7.74
Expert Solution & Answer
Trending nowThis is a popular solution!
Students have asked these similar questions
Peter propels a penguin with mass 10.0kg from 2.50m above the ground at an angle 30.0o from the horizontal axis (ground), with an initial speed of 15.0 m/s. Assuming the penguin remains rigid (scared, so assume the particle model!) and ignoring any rotational effects,
What is the maximum vertical height reached by the penguin?
a.
5.37 meters
b.
9.62 meters
c.
2.87 meters
d.
11.1 meters
In the game of tetherball a rope with length L=1.40 m connects a ball with mass m=0.600 kg to the top of a vertical pole so that the ball can spin around the pole as shown in the figure.
What is the speed ?v of the ball as it rotates around the pole when the angle θ of the rope is 30.0∘ with the vertical?
A matchbox car track begins at a height y=1.0, goes down hill to y=0, goes around a vertical loop of radius 0.2 m and then goes back up a smaller hill to end at a height y=0.3 m. The speed of the car at the end of the track is closest to which value?
Chapter 7 Solutions
College Physics
Ch. 7.1 - A rigid body is rotating counterclockwise about a...Ch. 7.1 - Suppose the change in angular position for each of...Ch. 7.2 - Consider again the pairs of angular positions for...Ch. 7.3 - Andrea and Chuck are riding on a merry-go-round....Ch. 7.3 - When the merry-go-round of Quick Quiz 7.4 is...Ch. 7.3 - A racetrack is constructed such that two arcs of...Ch. 7.3 - An object moves in a circular path with constant...Ch. 7.5 - A ball is falling toward the ground. Which of the...Ch. 7.5 - A planet has two moons with identical mass. Moon 1...Ch. 7.5 - Suppose an asteroid has a semimajor axis of 4 AU....
Ch. 7 - A disk rotates about an axis through its center....Ch. 7 - Suppose an alien civilization has a space station...Ch. 7 - If a cars wheels are replaced with wheels of...Ch. 7 - Objects moving along a circular path have a...Ch. 7 - A pendulum consists of a small object called a bob...Ch. 7 - Because of Earths rotation about its axis, you...Ch. 7 - It has been suggested that rotating cylinders...Ch. 7 - Describe the path of a moving object in the event...Ch. 7 - A pail of water can be whirled in a vertical...Ch. 7 - A car of mass m follows a truck of mass 2m around...Ch. 7 - Is it possible for a car to move in a circular...Ch. 7 - A child is practicing for a BMX race. His speed...Ch. 7 - An object executes circular motion with constant...Ch. 7 - Convert (a) 47.0 to radians, (b) 12.0 rad to...Ch. 7 - A bicycle tire is spinning clockwise at 2.50...Ch. 7 - The tires on a new compact car have a diameter of...Ch. 7 - A potters wheel moves uniformly from rest to an...Ch. 7 - A dentists drill starts from rest. After 3.20 s of...Ch. 7 - A centrifuge in a medical laboratory rotates at an...Ch. 7 - A bicyclist starting at rest produces a constant...Ch. 7 - A bicycle is turned upside down while its owner...Ch. 7 - The diameters of the main rotor and tail rotor of...Ch. 7 - The tub of a washer goes into its spin-dry cycle,...Ch. 7 - A car initially traveling at 29.0 m/s undergoes a...Ch. 7 - A 45.0-cm diameter disk rotates with a constant...Ch. 7 - A rotating wheel requires 3.00 s to rotate 37.0...Ch. 7 - An electric motor rotating a workshop grinding...Ch. 7 - A car initially traveling eastward turns north by...Ch. 7 - It has been suggested that rotating cylinders...Ch. 7 - (a) What is the tangential acceleration of a bug...Ch. 7 - An adventurous archeologist (m = 85.0 kg) tries to...Ch. 7 - One end of a cord is fixed and a small 0.500-kg...Ch. 7 - Human centrifuges are used to train military...Ch. 7 - A 55.0-kg ice skater is moving at 4.00 m/s when...Ch. 7 - A 40.0-kg child swings in a swing supported by two...Ch. 7 - A certain light truck can go around a flat curve...Ch. 7 - A sample of blood is placed in a centrifuge of...Ch. 7 - A 50.0-kg child stands at the rim of a...Ch. 7 - A space habitat for a long space voyage consists...Ch. 7 - An air puck of mass m1 = 0.25 kg is tied to a...Ch. 7 - A snowboarder drops from rest into a halfpipe of...Ch. 7 - A woman places her briefcase on the backseat of...Ch. 7 - A pail of water is rotated in a vertical circle of...Ch. 7 - A 40.0-kg child takes a ride on a Ferris wheel...Ch. 7 - Prob. 32PCh. 7 - (a) Find the magnitude of the gravitational force...Ch. 7 - The International Space Station has a mass of 4.19...Ch. 7 - A coordinate system (in meters) is constructed on...Ch. 7 - Prob. 36PCh. 7 - Objects with masses of 200. kg and 500. kg are...Ch. 7 - Use the data of Table 7.3 to find the point...Ch. 7 - Prob. 39PCh. 7 - Two objects attract each other with a...Ch. 7 - Prob. 41PCh. 7 - Prob. 42PCh. 7 - A satellite of Mars, called Phoebus, has an...Ch. 7 - Prob. 44PCh. 7 - A comet has a period of 76.3 years and moves in an...Ch. 7 - Additional Problems A synchronous satellite. which...Ch. 7 - (a) One of the moons of Jupiter, named Io, has an...Ch. 7 - Neutron stars are extremely dense objects that are...Ch. 7 - One method of pitching a softball is called the...Ch. 7 - A digital audio compact disc (CD) carries data...Ch. 7 - An athlete swings a 5.00-kg ball horizontally on...Ch. 7 - The dung beetle is known as one of the strongest...Ch. 7 - Prob. 53APCh. 7 - A 0.400-kg pendulum bob passes through the lowest...Ch. 7 - A car moves at speed v across a bridge made in the...Ch. 7 - Keratinocytes are the most common cells in the...Ch. 7 - Because of Earths rotation about its axis, a point...Ch. 7 - A roller coaster travels in a circular path, (a)...Ch. 7 - In Robert Heinleins The Moon Is a Harsh Mistress,...Ch. 7 - A model airplane of mass 0.750 kg flies with a...Ch. 7 - In a home laundry dryer, a cylindrical tub...Ch. 7 - Casting of molten metal is important in many...Ch. 7 - A skier starts at rest at the top of a large...Ch. 7 - A stuntman whose mass is 70 kg swings from the end...Ch. 7 - Suppose a 1 800-kg car passes over a bump in a...Ch. 7 - The pilot of an airplane executes a constant-speed...Ch. 7 - Prob. 67APCh. 7 - A coin rests 15.0 cm from the center of a...Ch. 7 - A 4.0-kg object is attached to a vertical rod by...Ch. 7 - A 0.275-kg object is swung in a vertical circular...Ch. 7 - (a) A luggage carousel at an airport has the form...Ch. 7 - The maximum lift force on a bat is proportional to...Ch. 7 - In a popular amusement park ride, a rotating...Ch. 7 - A massless spring of constant k = 78.4 N/m is...Ch. 7 - A 0.50-kg ball that is tied to the end of a 1.5-m...
Additional Science Textbook Solutions
Find more solutions based on key concepts
Planetary Priorities. Suppose you were in charge of developing and prioritizing future planetary missions for N...
Essential Cosmic Perspective
What discovery in the 15th century greatly advanced progress in science?
Conceptual Physical Science Explorations
42. * Insulating a house You insulate your house using insulation rated as R-12, which will conduct 1/12 Btu/h ...
College Physics
Given: W = 132 J t = 7.00 s p = ?
Applied Physics (11th Edition)
Why doesnt Earths rotation provide a suitable time standard?
Essential University Physics (3rd Edition)
A device for training astronauts and jet fighter pilots is designed to rotate the trainee in a horizontal circl...
Physics for Scientists and Engineers with Modern Physics
Knowledge Booster
Learn more about
Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, physics and related others by exploring similar questions and additional content below.Similar questions
- The coefficient of friction between mass m 1 and the surface is 0.15. The pulley is a disk and has a radius of 0.100 m and a mass of 0.25 kg. m 1 = 10.0 kg, m 2 = 20.0 kg.If the system is released from rest, find the final speed of each block when the hanging mass falls 2.0 m. ( I(disk)= 1/2 m R 2 )arrow_forwardA pendulum consists of a small object called a bob hanging from a light cord of fixed length, with the top end of the cord fixed, as represented in Figure OQ5.6. The bob moves without friction, swinging equally high on both sides. It moves from its turning point A through point B and reaches its maximum speed at point C. (a) Of these points, is there a point where the bob has nonzero radial acceleration and zero tangential acceleration? If so, which point? What is the direction of its total acceleration at this point? (b) Of these points, is there a point where the bob has nonzero tangential acceleration and zero radial acceleration? If so, which point? What is the direction of its total acceleration at this point? (c) Is there a point where the bob has no acceleration? If so, which point? (d) Is there a point where the bob has both nonzero tangential and radial acceleration? If so, which point? What is the direction of its total acceleration at this point? Figure OQ5.6arrow_forwardCase Study For each acceleration listed, state the position and velocity of the disk in Crall and Whipples experiment (Figs. 16.316.5). There may be more than one possible answer for each given acceleration. a. ay = 3.8 m/s2 b. ay = 3.8 m/s2 c. ay = 0arrow_forward
- As shown in Figure P8.20, a bullet of mass m and speed v passes completely through a pendulum bob of mass M. The bullet emerges with a speed of v/2. The pendulum bob is suspended by a stiff rod (not a string) of length , and negligible mass. What is the minimum value of v such that the pendulum bob will barely swing through a complete vertical circle? Figure P8.20arrow_forwardA space probe is fired as a projectile from the Earths surface with an initial speed of 2.00 104 m/s. What will its speed be when it is very far from the Earth? Ignore atmospheric friction and the rotation of the Earth. P11.26 Ki+Ui=Kf+Uf12mvi2+GMEm(1rf1ri)=12mvf212vi2+GME(01RE)=12vf2orvf2=v122GMEREandvf=(v122GMERE)1/2,vf=[(2.00104)21.25108]1/2m/s=1.66104m/sarrow_forwardThe mass of a hoop of radius 1.0 m is 6.0 kg. It rolls across a horizontal surface with a speed of 10.0 m/s. (a) How much work is required to stop the hoop? (b) If the hoop starts up a surface at 30 to the horizontal with a speed of 10.0 m/s, how far along the incline will it travel before stopping and rolling back down?arrow_forward
- A rod of length L=3.00 m and negligible mass, that can pivot about one end to rotate in a vertical circle. A ball of mass m = 10.0 kg is attached to the other end. The rod is pulled aside to angle θ0 = 70° and released with initial velocity ? = 5.00 m/s. (a) What is the speed of the ball at the lowest point? (b) what is the speed of the ball when θ = 10°?arrow_forwardA handful of professional skaters have taken a skateboard through an inverted loop in a full pipe. For a typical pipe with a diameter 13 feet, what is the minimum speed a 66 kg skater must have at the very top of the loop?arrow_forwardA small block with mass 0.0300 kgkg slides in a vertical circle of radius 0.425 mm on the inside of a circular track. During one of the revolutions of the block, when the block is at the bottom of its path, point AA, the magnitude of the normal force exerted on the block by the track has magnitude 3.90 NN . In this same revolution, when the block reaches the top of its path, point BB, the magnitude of the normal force exerted on the block has magnitude 0.675 NN . 1)How much work was done on the block by friction during the motion of the block from point AA to point BB?arrow_forward
- A hoop of radius 0.50m and a mass of 0.20 kg is relased from rest and allowed to roll down an inclined plane. How fast is it moving after dropping a vertical distance of 3.0m? I for a hoop is MR^2 A) 7.7m/s B) 5.4m/s C)2.2m/s D)3.8m/sarrow_forwardA 3.0-kg mass slides on a frictionless horizontal surface with a speed of 3.0 m / s when it collides with a 1.0-kg mass initially at rest as shown in the figure. The two masses stick to each other and slide on a frictionless circular wheel portion of radius 0.40 m. At what maximum height h, above the horizontal, do the masses reach? Answers: a) 0.18 m b) 0.15 m c) 0.21 m d) 0.26 m e) 0.40 marrow_forwardA 0.5-kg stone slides down a frictionless bowl, starting from rest at the rim. The bowl itself is a hemisphere of radius 0.100 m. Just as the stone reaches the bottom of the bowl, how fast is it moving?arrow_forward
arrow_back_ios
SEE MORE QUESTIONS
arrow_forward_ios
Recommended textbooks for you
College PhysicsPhysicsISBN:9781285737027Author:Raymond A. Serway, Chris VuillePublisher:Cengage Learning
College PhysicsPhysicsISBN:9781305952300Author:Raymond A. Serway, Chris VuillePublisher:Cengage Learning
Physics for Scientists and Engineers, Technology ...PhysicsISBN:9781305116399Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning
Principles of Physics: A Calculus-Based TextPhysicsISBN:9781133104261Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning
Physics for Scientists and Engineers with Modern ...PhysicsISBN:9781337553292Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning
Physics for Scientists and EngineersPhysicsISBN:9781337553278Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning
College Physics
Physics
ISBN:9781285737027
Author:Raymond A. Serway, Chris Vuille
Publisher:Cengage Learning
College Physics
Physics
ISBN:9781305952300
Author:Raymond A. Serway, Chris Vuille
Publisher:Cengage Learning
Physics for Scientists and Engineers, Technology ...
Physics
ISBN:9781305116399
Author:Raymond A. Serway, John W. Jewett
Publisher:Cengage Learning
Principles of Physics: A Calculus-Based Text
Physics
ISBN:9781133104261
Author:Raymond A. Serway, John W. Jewett
Publisher:Cengage Learning
Physics for Scientists and Engineers with Modern ...
Physics
ISBN:9781337553292
Author:Raymond A. Serway, John W. Jewett
Publisher:Cengage Learning
Physics for Scientists and Engineers
Physics
ISBN:9781337553278
Author:Raymond A. Serway, John W. Jewett
Publisher:Cengage Learning
What Is Circular Motion? | Physics in Motion; Author: GPB Education;https://www.youtube.com/watch?v=1cL6pHmbQ2c;License: Standard YouTube License, CC-BY