
Concept explainers
A pendulum consists of a small object called a bob hanging from a light cord of fixed length, with the top end of the cord fixed, as represented in Figure CQ7.5. The bob moves without friction, swinging equally high on both sides. It moves from its turning point A through point B and reaches its maximum speed at point C. (a) At what point does the bob have non-zero radial acceleration and zero tangential acceleration? What is the direction of its total acceleration at this point? (b) At what point does the bob have nonzero tangential acceleration and zero radial acceleration? What is the direction of its total acceleration at this point? (c) At what point does the bob have both nonzero tangential and radial acceleration? What is the direction of its total acceleration at this point?
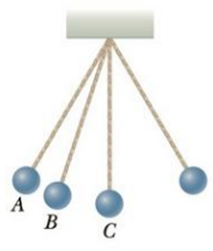
Figure CQ7.5
Trending nowThis is a popular solution!

Chapter 7 Solutions
College Physics
Additional Science Textbook Solutions
Integrated Science
College Physics
Glencoe Physics: Principles and Problems, Student Edition
The Cosmic Perspective Fundamentals (2nd Edition)
An Introduction to Thermal Physics
Glencoe Physical Science 2012 Student Edition (Glencoe Science) (McGraw-Hill Education)
- We place a 2.0 m long rod in a vertical position and let it fall. At what speed does the upper end of the rod fly against the horizontal floor, if its lower end doesnt move anywhere? (The solution is 7.7 m / s)arrow_forwardA 2.30 kg hoop 1.10 m in diameter is rolling to the right without slipping on a horizontal floor at a steady 2.90 rad/s. How fast is its center moving? What is the total kinetic energy of the hoop? Find the magnitude of the velocity vector of each of the following points, as viewed by a person at rest on the ground: (i) the highest point on the hoop; (ii) the lowest point on the hoop, (iii) a point on the right side of the hoop, midway between the top and the bottom.arrow_forwardIn the figure here, a solid brass ball of mass 0.371 g will roll smoothly along a loop-the-loop track when released from rest along the straight section. The circular loop has radius R = 0.14 m, and the ball has radius r << R.(a) What is h if the ball is on the verge of leaving the track when it reaches the top of the loop?(b) If the ball is released at height h = 4R, what is the magnitude of the horizontal force component acting on the ball at point Q?arrow_forward
- a solid ball rolls smoothly from rest (starting at height H = 6.0 m) until it leaves the horizontal section at the end of the track, at height h = 2.0 m. How far horizontally from point A does the ball hit the floor?arrow_forwardASAP PLS SHOW ALL WORK, VERY URGENT A uniform disk of mass 15.0 kg and radius 0.200 m is spinning around an axis through its center and perpendicular to the disk. Its angular velocity depends on time such that ω(t) = (3.00 rad/s2) t + (1.00 rad/s3)t2. a) What is the angular acceleration at t=2.00 s? (rad/s2) b) How many revolutions did the wheel make between t=0 and t=2.00 s ? c) How much work was done on the disk between t=0 and t=2.00 s? (J)arrow_forwardIn the figure, a solid 0.3 kg ball rolls smoothly from rest (starting at height H = 6.4 m) until it leaves the horizontal section at the end of the track, at height h = 1.5 m. How far horizontally from point A does the ball hit the floor? The answer is not 5.42.arrow_forward
- A solid sphere of mass 1 kg and radius = 0.1 m (I = MR2/2) rolls down an inclined plane of height = 1 m. Find the speed of the sphere when it reaches the bottom of the plane.arrow_forwardAt t = 0, a pulley rotating on a fixed axle with a constant acceleration has an initial angular velocity of 2.7 rad/sec. After 7.10 seconds, it has completed 16 revolutions. What is its angular acceleration in rad/sec^2? In the previous problem, what is the pulley's angular velocity at the end of the 7.10 seconds?arrow_forwardA 26 kg block hangs from a 350 g rotating solid disk. The radius of the disk is 12 cm. What is the speed of the block after it has dropped 55 cm starting from rest? If a disk with radius 5.0 cm is used instead, how does your answer change?arrow_forward
- The puck in Figure P11.46 has a mass of 0.120 kg. The distance of the puck from the center of rotation is originally 40.0 cm, and the puck is sliding with a speed of 80.0 cm/s. The string is pulled downward 15.0 cm through the hole in the frictionless table. Determine the work done on the puck. (Suggestion: Consider the change of kinetic energy.) Figure P11.46arrow_forwardA uniform rod of length b stands vertically upright on a rough floor and then tips over. What is the rods angular velocity when it hits the floor?arrow_forwardA space probe is fired as a projectile from the Earths surface with an initial speed of 2.00 104 m/s. What will its speed be when it is very far from the Earth? Ignore atmospheric friction and the rotation of the Earth. P11.26 Ki+Ui=Kf+Uf12mvi2+GMEm(1rf1ri)=12mvf212vi2+GME(01RE)=12vf2orvf2=v122GMEREandvf=(v122GMERE)1/2,vf=[(2.00104)21.25108]1/2m/s=1.66104m/sarrow_forward
 Principles of Physics: A Calculus-Based TextPhysicsISBN:9781133104261Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning
Principles of Physics: A Calculus-Based TextPhysicsISBN:9781133104261Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning Physics for Scientists and Engineers, Technology ...PhysicsISBN:9781305116399Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning
Physics for Scientists and Engineers, Technology ...PhysicsISBN:9781305116399Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning Physics for Scientists and Engineers with Modern ...PhysicsISBN:9781337553292Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning
Physics for Scientists and Engineers with Modern ...PhysicsISBN:9781337553292Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning Physics for Scientists and EngineersPhysicsISBN:9781337553278Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning
Physics for Scientists and EngineersPhysicsISBN:9781337553278Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning Classical Dynamics of Particles and SystemsPhysicsISBN:9780534408961Author:Stephen T. Thornton, Jerry B. MarionPublisher:Cengage Learning
Classical Dynamics of Particles and SystemsPhysicsISBN:9780534408961Author:Stephen T. Thornton, Jerry B. MarionPublisher:Cengage Learning




