
Calculus (MindTap Course List)
8th Edition
ISBN: 9781285740621
Author: James Stewart
Publisher: Cengage Learning
expand_more
expand_more
format_list_bulleted
Concept explainers
Textbook Question
Chapter 4.4, Problem 65E
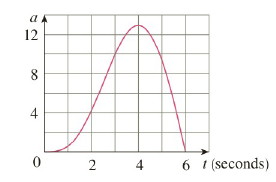
The graph of the acceleration
Expert Solution & Answer
Trending nowThis is a popular solution!

Chapter 4 Solutions
Calculus (MindTap Course List)
Ch. 4.1 - Prob. 1ECh. 4.1 - a Use six rectangles to find estimates of each...Ch. 4.1 - a Estimate the area under the graph of f(x)=1/x...Ch. 4.1 - Prob. 4ECh. 4.1 - Prob. 5ECh. 4.1 - Prob. 6ECh. 4.1 - Prob. 7ECh. 4.1 - Evaluate the upper and lower sums for...Ch. 4.1 - With a programmable calculator or a computer, it...Ch. 4.1 - Prob. 10E
Ch. 4.1 - Some computer algebra systems have commands that...Ch. 4.1 - Prob. 12ECh. 4.1 - The speed of a runner increased steadily during...Ch. 4.1 - The table shows speedometer readings at 10-second...Ch. 4.1 - Prob. 15ECh. 4.1 - Prob. 16ECh. 4.1 - The velocity graph of a braking car is shown. Use...Ch. 4.1 - Prob. 18ECh. 4.1 - In someone infected with measles, the virus level...Ch. 4.1 - The table shows the number of people per day who...Ch. 4.1 - Use Definition 2 to find an expression for the...Ch. 4.1 - Use Definition 2 to find an expression for the...Ch. 4.1 - Use Definition 2 to find an expression for the...Ch. 4.1 - Prob. 24ECh. 4.1 - Determine a region whose area is equal to the...Ch. 4.1 - a Use Definition 2 to find an expression for the...Ch. 4.1 - Prob. 27ECh. 4.1 - Prob. 28ECh. 4.1 - Prob. 29ECh. 4.1 - Prob. 30ECh. 4.1 - Prob. 31ECh. 4.1 - Prob. 32ECh. 4.2 - Evaluate the Riemann sum for f(x)=x1,6x4, with...Ch. 4.2 - If f(x)=cosx0x3/4 evaluate the Riemann sum with n...Ch. 4.2 - If f(x)=x24,0x3, find the Riemann sum with n = 6,...Ch. 4.2 - a Find the Riemann sum for f(x)=1/x,1x2, with four...Ch. 4.2 - The graph of a function f is given. Estimate...Ch. 4.2 - The graph of g is shown. Estimate 24g(x)dx with...Ch. 4.2 - Prob. 7ECh. 4.2 - The table gives the values of a function obtained...Ch. 4.2 - Use the Midpoint Rule with the given value of n to...Ch. 4.2 - Use the Midpoint Rule with the given value of n to...Ch. 4.2 - Use the Midpoint Rule with the given value of n to...Ch. 4.2 - Use the Midpoint Rule with the given value of n to...Ch. 4.2 - If you have a CAS that evaluates midpoint...Ch. 4.2 - With a programmable calculator or computer see the...Ch. 4.2 - Prob. 15ECh. 4.2 - Prob. 16ECh. 4.2 - Prob. 17ECh. 4.2 - Prob. 18ECh. 4.2 - Express the limit as a definite integral on the...Ch. 4.2 - Express the limit as a definite integral on the...Ch. 4.2 - Prob. 21ECh. 4.2 - Prob. 22ECh. 4.2 - Use the form of the definition of the integral...Ch. 4.2 - Prob. 24ECh. 4.2 - Prob. 25ECh. 4.2 - Prob. 26ECh. 4.2 - Prove that abxdx=b2a22Ch. 4.2 - Prove that abx2dx=b3a33Ch. 4.2 - Prob. 29ECh. 4.2 - Express the integral as a limit of Riemann sums....Ch. 4.2 - Prob. 31ECh. 4.2 - Express the integral as a limit of sums. Then...Ch. 4.2 - The graph of f is shown. Evaluate each integral by...Ch. 4.2 - The graph of g consists of two straight fines and...Ch. 4.2 - Evaluate the integral by interpreting it in terms...Ch. 4.2 - Evaluate the integral by interpreting it in terms...Ch. 4.2 - Prob. 37ECh. 4.2 - Prob. 38ECh. 4.2 - Evaluate the integral by interpreting it in terms...Ch. 4.2 - Prob. 40ECh. 4.2 - Prob. 41ECh. 4.2 - Given that 0sin4xdx=38, what is 0sin4d?Ch. 4.2 - Prob. 43ECh. 4.2 - Prob. 44ECh. 4.2 - Prob. 45ECh. 4.2 - Prob. 46ECh. 4.2 - Prob. 47ECh. 4.2 - If 28f(x)dx=7.3 and 24f(x)dx=5.9, find 48f(x)dx.Ch. 4.2 - If 09f(x)dx=37 and 09g(x)dx=16, find...Ch. 4.2 - Find 05f(x)dx if f(x)={3forx3xforx3Ch. 4.2 - For the function / whose graph is shown, list the...Ch. 4.2 - If F(x)=2xf(t)dt, where f is the function whose...Ch. 4.2 - Each of the regions A, B, and C bounded by the...Ch. 4.2 - Suppose / has absolute minimum value m and...Ch. 4.2 - Use the properties of integrals to verify the...Ch. 4.2 - Use the properties of integrals to verify the...Ch. 4.2 - Prob. 57ECh. 4.2 - Prob. 58ECh. 4.2 - Prob. 59ECh. 4.2 - Prob. 60ECh. 4.2 - Prob. 61ECh. 4.2 - Use Property 8 of integrals to estimate the value...Ch. 4.2 - Prob. 63ECh. 4.2 - Prob. 64ECh. 4.2 - Use properties of integrals, together with...Ch. 4.2 - Prob. 66ECh. 4.2 - Prob. 67ECh. 4.2 - Prob. 68ECh. 4.2 - Prob. 69ECh. 4.2 - Prob. 70ECh. 4.2 - Let f(x)=0 if x is any rational number and f(x)=1...Ch. 4.2 - Prob. 72ECh. 4.2 - Express the limit as a definite intergal....Ch. 4.2 - Prob. 74ECh. 4.2 - Find 12x2dx. Hint: Choose xi* to be the geometric...Ch. 4.3 - Explain exactly what is meant by the statement...Ch. 4.3 - Let g(x)=0xf(t)dt, where f is the function whose...Ch. 4.3 - Let g(x)=0xf(t)dt, where f is the function whose...Ch. 4.3 - Let g(x)=0xf(t)dt where f is the function whose...Ch. 4.3 - Sketch the area represented by g(x). Then find...Ch. 4.3 - Sketch the area represented by g(x). Then find...Ch. 4.3 - Prob. 7ECh. 4.3 - Use Part 1 of the Fundamental Theorem of Calculus...Ch. 4.3 - Use Part 1 of the Fundamental Theorem of Calculus...Ch. 4.3 - Use Part 1 of the Fundamental Theorem of Calculus...Ch. 4.3 - Use Part 1 of the Fundamental Theorem of Calculus...Ch. 4.3 - Use Part 1 of the Fundamental Theorem of Calculus...Ch. 4.3 - Use Part 1 of the Fundamental Theorem of Calculus...Ch. 4.3 - Use Part 1 of the Fundamental Theorem of Calculus...Ch. 4.3 - Use Part 1 of the Fundamental Theorem of Calculus...Ch. 4.3 - Prob. 16ECh. 4.3 - Prob. 17ECh. 4.3 - Prob. 18ECh. 4.3 - Prob. 19ECh. 4.3 - Evaluate the integral. 11x100dxCh. 4.3 - Prob. 21ECh. 4.3 - Prob. 22ECh. 4.3 - Prob. 23ECh. 4.3 - Prob. 24ECh. 4.3 - Evaluate the integral. /6sindCh. 4.3 - Evaluate the integral. 55dxCh. 4.3 - Prob. 27ECh. 4.3 - Evaluate the integral. 04(4t)tdtCh. 4.3 - Evaluate the integral. 142+x2xdxCh. 4.3 - Evaluate the integral. 12(3u2)(u+1)duCh. 4.3 - Prob. 31ECh. 4.3 - Evaluate the integral. /4/3csc2dCh. 4.3 - Prob. 33ECh. 4.3 - Evaluate the integral. 12s2+1s2dsCh. 4.3 - Evaluate the integral. 12v5+3v6v4dvCh. 4.3 - Prob. 36ECh. 4.3 - Prob. 37ECh. 4.3 - Prob. 38ECh. 4.3 - Prob. 39ECh. 4.3 - Prob. 40ECh. 4.3 - Prob. 41ECh. 4.3 - Prob. 42ECh. 4.3 - Prob. 43ECh. 4.3 - Prob. 44ECh. 4.3 - Prob. 45ECh. 4.3 - Prob. 46ECh. 4.3 - Evaluate the integral and interpret it as a...Ch. 4.3 - Prob. 48ECh. 4.3 - What is wrong with the equation? 21x4dx=x33]21=38Ch. 4.3 - What is wrong with the equation? 124x3dx=2x2]12=32Ch. 4.3 - Prob. 51ECh. 4.3 - What is wrong with the equation? 0sec2xdx=tanx]0=0Ch. 4.3 - Find the derivative of the function....Ch. 4.3 - Prob. 54ECh. 4.3 - Prob. 55ECh. 4.3 - Prob. 56ECh. 4.3 - Let F(x)=xcosttdt. Find an equation of the tangent...Ch. 4.3 - Prob. 58ECh. 4.3 - On what interval is the curve y=0xt2t2+t+2dt...Ch. 4.3 - Let F(x)=1xf(t)dt, where f is the function whose...Ch. 4.3 - Prob. 61ECh. 4.3 - Prob. 62ECh. 4.3 - The Fresnel function S was defined in Example 3...Ch. 4.3 - The sine integral function Si(x)=0xsinttdt is...Ch. 4.3 - Let g(x)=0xf(t)dt where f is the function whose...Ch. 4.3 - Let g(x)=0xf(t)dt where f is the function whose...Ch. 4.3 - Evaluate the limit by first recognizing the sum as...Ch. 4.3 - Evaluate the limit by first recognizing the sum as...Ch. 4.3 - Prob. 69ECh. 4.3 - Prob. 70ECh. 4.3 - a Show that 11+x31+x3forx0 b Show that...Ch. 4.3 - Prob. 72ECh. 4.3 - Show that 0510x2x4+x2+1dx0.1 by comparing the...Ch. 4.3 - Let f(x)={0ifx0xif0x12xif1x20ifx2 and...Ch. 4.3 - Prob. 75ECh. 4.3 - Prob. 76ECh. 4.3 - A manufacturing company owns a major piece of...Ch. 4.3 - Prob. 78ECh. 4.3 - The following exercises are intended only for...Ch. 4.3 - The following exercises are intended only for...Ch. 4.3 - Prob. 81ECh. 4.3 - Prob. 82ECh. 4.3 - Prob. 83ECh. 4.3 - Prob. 84ECh. 4.4 - Verify by differentiation that the formula is...Ch. 4.4 - Verify by differentiation that the formula is...Ch. 4.4 - Verify by differentiation that the formula is...Ch. 4.4 - Verify by differentiation that the formula is...Ch. 4.4 - Prob. 5ECh. 4.4 - Prob. 6ECh. 4.4 - Find the general indefinite integral....Ch. 4.4 - Prob. 8ECh. 4.4 - Find the general indefinite integral....Ch. 4.4 - Prob. 10ECh. 4.4 - Prob. 11ECh. 4.4 - Prob. 12ECh. 4.4 - Prob. 13ECh. 4.4 - Prob. 14ECh. 4.4 - Find the general indefinite integral....Ch. 4.4 - Prob. 16ECh. 4.4 - Prob. 17ECh. 4.4 - Prob. 18ECh. 4.4 - Prob. 19ECh. 4.4 - Prob. 20ECh. 4.4 - Prob. 21ECh. 4.4 - Prob. 22ECh. 4.4 - Prob. 23ECh. 4.4 - Evaluate the integral. 11t(1t)2dtCh. 4.4 - Prob. 25ECh. 4.4 - Prob. 26ECh. 4.4 - Prob. 27ECh. 4.4 - Prob. 28ECh. 4.4 - Prob. 29ECh. 4.4 - Prob. 30ECh. 4.4 - Prob. 31ECh. 4.4 - Prob. 32ECh. 4.4 - Prob. 33ECh. 4.4 - Prob. 34ECh. 4.4 - Prob. 35ECh. 4.4 - Prob. 36ECh. 4.4 - Prob. 37ECh. 4.4 - Prob. 38ECh. 4.4 - Evaluate the integral. 25|x3|dxCh. 4.4 - Prob. 40ECh. 4.4 - Prob. 41ECh. 4.4 - Prob. 42ECh. 4.4 - Use a graph to estimate the x-intercepts of the...Ch. 4.4 - Prob. 44ECh. 4.4 - The area of the region that lies to the right of...Ch. 4.4 - The boundaries of the shaded region in the figure...Ch. 4.4 - Prob. 47ECh. 4.4 - Prob. 48ECh. 4.4 - Prob. 49ECh. 4.4 - A honeybee population starts with 100 bees and...Ch. 4.4 - Prob. 51ECh. 4.4 - Prob. 52ECh. 4.4 - Prob. 53ECh. 4.4 - Prob. 54ECh. 4.4 - The velocity function in meters per second is...Ch. 4.4 - Prob. 56ECh. 4.4 - The acceleration function in m/s2 and the initial...Ch. 4.4 - Prob. 58ECh. 4.4 - Prob. 59ECh. 4.4 - Prob. 60ECh. 4.4 - Prob. 61ECh. 4.4 - Suppose that a volcano is erupting and readings of...Ch. 4.4 - Lake Lanier in Georgia, USA, is a reservoir...Ch. 4.4 - Prob. 64ECh. 4.4 - The graph of the acceleration a(t) of a car...Ch. 4.4 - Shown is the graph of traffic on an Internet...Ch. 4.4 - Prob. 67ECh. 4.4 - Prob. 68ECh. 4.4 - Prob. 69ECh. 4.4 - Prob. 70ECh. 4.4 - Prob. 71ECh. 4.4 - Prob. 72ECh. 4.4 - Prob. 73ECh. 4.4 - The area labeled B is three times the area labeled...Ch. 4.5 - Evaluate the integral by making the given...Ch. 4.5 - Evaluate the integral by making the given...Ch. 4.5 - Prob. 3ECh. 4.5 - Evaluate the integral by making the given...Ch. 4.5 - Prob. 5ECh. 4.5 - Evaluate the integral by making the given...Ch. 4.5 - Prob. 7ECh. 4.5 - Evaluate the indefinite integral. x2sin(x3)dxCh. 4.5 - Prob. 9ECh. 4.5 - Evaluate the indefinite integral. sin1+costdtCh. 4.5 - Evaluate the indefinite integral. sin(2/3)dCh. 4.5 - Evaluate the indefinite integral. sec22dCh. 4.5 - Prob. 13ECh. 4.5 - Evaluate the indefinite integral. y2(4y3)2/3dyCh. 4.5 - Prob. 15ECh. 4.5 - Prob. 16ECh. 4.5 - Prob. 17ECh. 4.5 - Prob. 18ECh. 4.5 - Prob. 19ECh. 4.5 - Prob. 20ECh. 4.5 - Prob. 21ECh. 4.5 - Prob. 22ECh. 4.5 - Prob. 23ECh. 4.5 - Prob. 24ECh. 4.5 - Prob. 25ECh. 4.5 - Evaluate the indefinite integral. sec2xtan2xdxCh. 4.5 - Evaluate the indefinite integral. sec3xtanxdxCh. 4.5 - Prob. 28ECh. 4.5 - Evaluate the indefinite integral. x(2x+5)8dxCh. 4.5 - Prob. 30ECh. 4.5 - Evaluate the indefinite integral. Illustrate and...Ch. 4.5 - Prob. 32ECh. 4.5 - Evaluate the indefinite integral. Illustrate and...Ch. 4.5 - Evaluate the indefinite integral. Illustrate and...Ch. 4.5 - Prob. 35ECh. 4.5 - Prob. 36ECh. 4.5 - Evaluate the definite integral. 011+7x3dxCh. 4.5 - Prob. 38ECh. 4.5 - Evaluate the integral. 0/6sintcos2tdtCh. 4.5 - Prob. 40ECh. 4.5 - Evaluate the definite integral. /4/4(x3+x4tanx)dxCh. 4.5 - Prob. 42ECh. 4.5 - Prob. 43ECh. 4.5 - Prob. 44ECh. 4.5 - Prob. 45ECh. 4.5 - Evaluate the definite integral. /3/3x4sinxdxCh. 4.5 - Evaluate the definite integral. 12xx1dxCh. 4.5 - Prob. 48ECh. 4.5 - Evaluate the definite integral. 1/21cos(x2)x3dxCh. 4.5 - Prob. 50ECh. 4.5 - Evaluate the definite integral. 01dx(1+x)4Ch. 4.5 - Prob. 52ECh. 4.5 - Prob. 53ECh. 4.5 - Prob. 54ECh. 4.5 - Prob. 55ECh. 4.5 - Prob. 56ECh. 4.5 - Prob. 57ECh. 4.5 - Prob. 58ECh. 4.5 - Prob. 59ECh. 4.5 - Prob. 60ECh. 4.5 - Prob. 61ECh. 4.5 - If f is continuous function on , prove that...Ch. 4.5 - If a and b are positive numbers, show that...Ch. 4.5 - Prob. 64ECh. 4.5 - Prob. 65ECh. 4.5 - Prob. 66ECh. 4.5 - Prob. 67ECh. 4.5 - Prob. 68ECh. 4.5 - Prob. 69ECh. 4.5 - Prob. 70ECh. 4.5 - Prob. 71ECh. 4.5 - Prob. 72ECh. 4.5 - Prob. 73ECh. 4.5 - Prob. 74ECh. 4.5 - Prob. 75ECh. 4.5 - Prob. 76ECh. 4.5 - Prob. 77ECh. 4.5 - Prob. 78ECh. 4.5 - Prob. 79ECh. 4.5 - Prob. 80ECh. 4.5 - Prob. 81ECh. 4.5 - Prob. 82ECh. 4.5 - Prob. 83ECh. 4.5 - Prob. 84ECh. 4.5 - Prob. 85ECh. 4.R - a Write an expression for a Riemann sum of a...Ch. 4.R - a Write the definition of the definite integral of...Ch. 4.R - Prob. 3CCCh. 4.R - Prob. 4CCCh. 4.R - Prob. 5CCCh. 4.R - Prob. 6CCCh. 4.R - a Explain the meaning of the indefinite integral...Ch. 4.R - Explain exactly what is meant by the statement...Ch. 4.R - State the Substitution Rule. In practice, how do...Ch. 4.R - Prob. 1TFQCh. 4.R - Prob. 2TFQCh. 4.R - Prob. 3TFQCh. 4.R - Prob. 4TFQCh. 4.R - Prob. 5TFQCh. 4.R - Prob. 6TFQCh. 4.R - Prob. 7TFQCh. 4.R - Prob. 8TFQCh. 4.R - Prob. 9TFQCh. 4.R - Prob. 10TFQCh. 4.R - Prob. 11TFQCh. 4.R - Prob. 12TFQCh. 4.R - Prob. 13TFQCh. 4.R - Prob. 14TFQCh. 4.R - Prob. 15TFQCh. 4.R - Prob. 16TFQCh. 4.R - Prob. 17TFQCh. 4.R - Prob. 18TFQCh. 4.R - Use the given graph of f to find the Riemann sum...Ch. 4.R - a Evaluate the Riemann sum for f(x)=x2x0x2 With...Ch. 4.R - Prob. 3ECh. 4.R - Prob. 4ECh. 4.R - Prob. 5ECh. 4.R - Prob. 6ECh. 4.R - Prob. 7ECh. 4.R - Prob. 8ECh. 4.R - The graph of f consists of the three line segments...Ch. 4.R - Prob. 10ECh. 4.R - Prob. 11ECh. 4.R - Prob. 12ECh. 4.R - Prob. 13ECh. 4.R - Prob. 14ECh. 4.R - Prob. 15ECh. 4.R - Prob. 16ECh. 4.R - Prob. 17ECh. 4.R - Prob. 18ECh. 4.R - Evaluate the integral, if it exists. 15dt(t4)2Ch. 4.R - Prob. 20ECh. 4.R - Prob. 21ECh. 4.R - Prob. 22ECh. 4.R - Prob. 23ECh. 4.R - Prob. 24ECh. 4.R - Prob. 25ECh. 4.R - Prob. 26ECh. 4.R - Prob. 27ECh. 4.R - Prob. 28ECh. 4.R - Evaluate the integral, if it exists. 03|x24|dxCh. 4.R - Prob. 30ECh. 4.R - Prob. 31ECh. 4.R - Prob. 32ECh. 4.R - Prob. 33ECh. 4.R - Prob. 34ECh. 4.R - Prob. 35ECh. 4.R - Prob. 36ECh. 4.R - Prob. 37ECh. 4.R - Find the derivative of the function....Ch. 4.R - Find the derivative of the function. y=xxcosdCh. 4.R - Prob. 40ECh. 4.R - Prob. 41ECh. 4.R - Prob. 42ECh. 4.R - Prob. 43ECh. 4.R - Prob. 44ECh. 4.R - Prob. 45ECh. 4.R - Prob. 46ECh. 4.R - Prob. 47ECh. 4.R - Prob. 48ECh. 4.R - Prob. 49ECh. 4.R - Let f(x)={x1if3x01x2if0x1 Evaluate 31f(x)dx by...Ch. 4.R - Prob. 51ECh. 4.R - The Fresnel function S(x)=0xsin(12t2)dt was...Ch. 4.R - Prob. 53ECh. 4.R - Prob. 54ECh. 4.R - Prob. 55ECh. 4.R - Find limh01h22+h1+t3dtCh. 4.R - Prob. 57ECh. 4.R - Prob. 58ECh. 4.P - If xsinxx=0x2f(t)dt, where f is a continuous...Ch. 4.P - Prob. 2PCh. 4.P - If f is a differentiable function such that f(x)...Ch. 4.P - Prob. 4PCh. 4.P - Prob. 5PCh. 4.P - Prob. 6PCh. 4.P - Prob. 7PCh. 4.P - Prob. 8PCh. 4.P - Prob. 9PCh. 4.P - Prob. 10PCh. 4.P - Suppose the coefficients of the cubic polynomial...Ch. 4.P - Prob. 12PCh. 4.P - Prob. 13PCh. 4.P - The figure shows a parabolic segment, that is, a...Ch. 4.P - Given the point a, b in the first quadrant, find...Ch. 4.P - The figure shows a region consisting of all points...Ch. 4.P - Prob. 17PCh. 4.P - For any number c, we let fc(x) be the smaller of...
Knowledge Booster
Learn more about
Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, calculus and related others by exploring similar questions and additional content below.Similar questions
Recommended textbooks for you
 Big Ideas Math A Bridge To Success Algebra 1: Stu...AlgebraISBN:9781680331141Author:HOUGHTON MIFFLIN HARCOURTPublisher:Houghton Mifflin Harcourt
Big Ideas Math A Bridge To Success Algebra 1: Stu...AlgebraISBN:9781680331141Author:HOUGHTON MIFFLIN HARCOURTPublisher:Houghton Mifflin Harcourt Trigonometry (MindTap Course List)TrigonometryISBN:9781337278461Author:Ron LarsonPublisher:Cengage Learning
Trigonometry (MindTap Course List)TrigonometryISBN:9781337278461Author:Ron LarsonPublisher:Cengage Learning
 Algebra and Trigonometry (MindTap Course List)AlgebraISBN:9781305071742Author:James Stewart, Lothar Redlin, Saleem WatsonPublisher:Cengage Learning
Algebra and Trigonometry (MindTap Course List)AlgebraISBN:9781305071742Author:James Stewart, Lothar Redlin, Saleem WatsonPublisher:Cengage Learning Functions and Change: A Modeling Approach to Coll...AlgebraISBN:9781337111348Author:Bruce Crauder, Benny Evans, Alan NoellPublisher:Cengage Learning
Functions and Change: A Modeling Approach to Coll...AlgebraISBN:9781337111348Author:Bruce Crauder, Benny Evans, Alan NoellPublisher:Cengage Learning

Big Ideas Math A Bridge To Success Algebra 1: Stu...
Algebra
ISBN:9781680331141
Author:HOUGHTON MIFFLIN HARCOURT
Publisher:Houghton Mifflin Harcourt

Trigonometry (MindTap Course List)
Trigonometry
ISBN:9781337278461
Author:Ron Larson
Publisher:Cengage Learning


Algebra and Trigonometry (MindTap Course List)
Algebra
ISBN:9781305071742
Author:James Stewart, Lothar Redlin, Saleem Watson
Publisher:Cengage Learning

Functions and Change: A Modeling Approach to Coll...
Algebra
ISBN:9781337111348
Author:Bruce Crauder, Benny Evans, Alan Noell
Publisher:Cengage Learning
Learn Algebra 6 : Rate of Change; Author: Derek Banas;https://www.youtube.com/watch?v=Dw701mKcJ1k;License: Standard YouTube License, CC-BY