
An astronaut in her space suit has a total mass of 87.0 kg, including suit and oxygen tank. Her tether line loses its attachment to her spacecraft while she’s on a spacewalk. Initially at rest with respect to her spacecraft, she throws her 12.0-kg oxygen tank away from her spacecraft with a speed of 8.00 m/s to propel herself back toward it (Fig. P6.29).
(a) Determine the maximum distance she can be from the craft and still return within 2.00 min (the amount of time the air in her helmet remains breathable), (b) Explain in terms of Newton’s laws of motion why this strategy works.
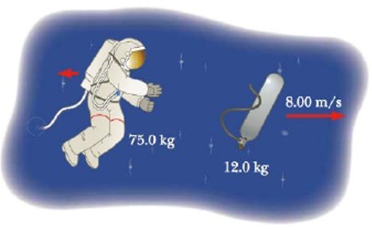
Figure P6.29
Trending nowThis is a popular solution!

Chapter 6 Solutions
College Physics
Additional Science Textbook Solutions
The Physics of Everyday Phenomena
University Physics Volume 3
Sears And Zemansky's University Physics With Modern Physics
Conceptual Physics (12th Edition)
Physics of Everyday Phenomena
The Cosmic Perspective (8th Edition)
- What exhaust speed is required to accelerate a rocket in deep space from 800 m/s to 1000 m/s in 5.0 s if the total rocket mass is 1200 kg and the rocket only has 50 kg of fuel left?arrow_forwardA rocket has total mass Mi = 360 kg, including Mfuel = 330 kg of fuel and oxidizer. In interstellar space, it starts from rest at the position x = 0, turns on its engine at time t = 0, and puts out exhaust with relative speed ve = 1 500 m/s at the constant rate k = 2.50 kg/s. The fuel will last for a burn time of Tb = Mfuel/k = 330 kg/(2.5 kg/s) = 132 s. (a) Show that during the burn the velocity of the rocket as a function of time is given by v(t)=veln(1ktMi) (b) Make a graph of the velocity of the rocket as a function of time for times running from 0 to 132 s. (c) Show that the acceleration of the rocket is a(t)=kveMikt (d) Graph the acceleration as a function of time. (c) Show that the position of the rocket is x(t)=ve(Mikt)ln(1ktMi)+vet (f) Graph the position during the burn as a function of time.arrow_forwardA cannon is rigidly attached to a carriage, which can move along horizontal rails but is connected to a post by a large spring, initially unstretchcd and with force constant k = 2.00 104 N/m, as shown in Figure P8.60. The cannon fires a 200-kg projectile at a velocity of 125 m/s directed 45.0 above the horizontal. (a) Assuming that the mass of the cannon and its carriage is 5 000 kg, find the recoil speed of the cannon. (b) Determine the maximum extension of the spring. (c) Find the maximum force the spring exerts on the carriage. (d) Consider the system consisting of the cannon, carriage, and projectile. Is the momentum of this system conserved during the firing? Why or why not?arrow_forward
- A hockey puck of mass 150 g is sliding due east on a frictionless table with a speed of 10 m/s. Suddenly, a constant force of magnitude 5 N and direction due north is applied to the puck for 1.5 s. Find the north and east components of the momentum at the end of the 1.3-s interval.arrow_forwardA 2000-kg railway freight car coasts at 4.4 m/s underneath a grain terminal, which dumps grain directly down into the freight car. If the speed of the loaded freight car must not go below 3.0 m/s, what is the maximum mass of grain that it can accept?arrow_forwardA mother pushes her son in a stroller at a constant speed of 1.52 m/s. The boy tosses a 56.7-g tennis ball straight up at 1.75 m/s and catches it. The boys father sits on a bench and watches. a. According to the mother, what are the balls initial and final momenta? b. According to the father, what are the balls initial and final momenta? c. According to the mother, is the balls momentum ever zero? If so, when? If not, why not? d. According to the father, is the balls momentum ever zero? If so, when? If not, why not?arrow_forward
- Sand from a stationary hopper falls onto a moving conveyor belt at the rate of 5.00 kg/s as shown in Figure P8.64. The conveyor belt is supported by frictionless rollers and moves at a constant speed of v = 0.750 m/s under the action of a constant horizontal external force Fext supplied by the motor that drives the belt. Find (a) the sands rate of change of momentum in the horizontal direction, (b) the force of friction exerted by the belt on the sand, (c) the external force Fext, (d) the work done by Fext in 1 s, and (e) the kinetic energy acquired by the falling sand each second due to the change in its horizontal motion. (f) Why are the answers to parts (d) and (e) different? Figure P8.64arrow_forwardA space probe, initially at rest, undergoes an internal mechanical malfunction and breaks into three pieces. One piece of mass ml = 48.0 kg travels in the positive x-direction at 12.0 m/s, and a second piece of mass m2 = 62.0 kg travels in the xy-plane at an angle of 105 at 15.0 m/s. The third piece has mass m3 = 112 kg. (a) Sketch a diagram of the situation, labeling the different masses and their velocities, (b) Write the general expression for conservation of momentum in the x- and y-directions in terms of m1, m2, m3, v1, v2 and v3 and the sines and cosines of the angles, taking to be the unknown angle, (c) Calculate the final x-components of the momenta of m1 and m2. (d) Calculate the final y-components of the momenta of m1 and m2. (e) Substitute the known momentum components into the general equations of momentum for the x- and y-directions, along with the known mass m3. (f) Solve the two momentum equations for v3 cos and v3 sin , respectively, and use the identity cos2 + sin2 = 1 to obtain v3. (g) Divide the equation for v3 sin by that for v3 cos to obtain tan , then obtain the angle by taking the inverse tangent of both sides, (h) In general, would three such pieces necessarily have to move in the same plane? Why?arrow_forwardA girl of mass mg is standing on a plank of mass mp. Both are originally at rest on a frozen lake that constitutes a frictionless, flat surface. The girl begins to walk along the plank at a constant velocity vgp to the right relative to the plank. (The subscript gp denotes the girl relative to plank.) (a) What is the velocity vpi of the plank relative to the surface of the ice? (b) What is the girls velocity vgi relative to the ice surface?arrow_forward
- You hold a slingshot at arms length, pull the light elastic band back to your chin, and release it to launch a pebble horizontally with speed 200 cm/s. With the same procedure, you fire a bean with speed 600 cm/s. What is the ratio of the mass of the bean to the mass of the pebble? (a) 19 (b) 13 (c) 1 (d) 3 (e) 9arrow_forwardA water molecule consists of an oxygen atom with two hydrogen atoms bound to it (Fig. P8.36). The angle between the two bonds is 106. If the bonds are 0.100 nm long, where is the center of mass of the molecule? Figure P8.36arrow_forwardTwo bumper cars at the county fair are sliding toward one another (Fig. P11.54). Initially, bumper car 1 is traveling to the east at 5.62 m/s, and bumper car 2 is traveling 60.0 south of west at 10.00 m/s. They collide and stick together, as the driver of one car reaches out and grabs hold of the other driver. The two bumper cars move off together after the collision, and friction is negligible between the cars and the ground. a. If the masses of bumper cars 1 and 2 are 596 kg and 625 kg respectively, what is the velocity of the bumper cars immediately after the collision? b. What is the kinetic energy lost in the collision? c. Compare your answers to part (b) from this and Problem 54. Is one answer larger than the other? Discuss and explain any differences you find.arrow_forward
 Principles of Physics: A Calculus-Based TextPhysicsISBN:9781133104261Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning
Principles of Physics: A Calculus-Based TextPhysicsISBN:9781133104261Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning Physics for Scientists and EngineersPhysicsISBN:9781337553278Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning
Physics for Scientists and EngineersPhysicsISBN:9781337553278Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning Physics for Scientists and Engineers with Modern ...PhysicsISBN:9781337553292Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning
Physics for Scientists and Engineers with Modern ...PhysicsISBN:9781337553292Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning Physics for Scientists and Engineers: Foundations...PhysicsISBN:9781133939146Author:Katz, Debora M.Publisher:Cengage Learning
Physics for Scientists and Engineers: Foundations...PhysicsISBN:9781133939146Author:Katz, Debora M.Publisher:Cengage Learning Classical Dynamics of Particles and SystemsPhysicsISBN:9780534408961Author:Stephen T. Thornton, Jerry B. MarionPublisher:Cengage Learning
Classical Dynamics of Particles and SystemsPhysicsISBN:9780534408961Author:Stephen T. Thornton, Jerry B. MarionPublisher:Cengage Learning College PhysicsPhysicsISBN:9781285737027Author:Raymond A. Serway, Chris VuillePublisher:Cengage Learning
College PhysicsPhysicsISBN:9781285737027Author:Raymond A. Serway, Chris VuillePublisher:Cengage Learning





