
Concept explainers
A cylinder with moment of inertia I1 rotates with
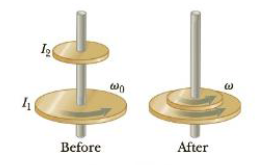
Figure P8.73
Trending nowThis is a popular solution!

Chapter 8 Solutions
College Physics
Additional Science Textbook Solutions
College Physics: A Strategic Approach (3rd Edition)
Physics (5th Edition)
Tutorials in Introductory Physics
Schaum's Outline of College Physics, Twelfth Edition (Schaum's Outlines)
The Cosmic Perspective Fundamentals (2nd Edition)
Conceptual Integrated Science
- A disk with moment of inertia I1 rotates about a frictionless, vertical axle with angular speed i. A second disk, this one having moment of inertia I2 and initially not rotating, drops onto the first disk (Fig. P10.50). Because of friction between the surfaces, the two eventually reach the same angular speed f. (a) Calculate f. (b) Calculate the ratio of the final to the initial rotational energy. Figure P10.50arrow_forwardTwo astronauts (Fig. P10.67), each having a mass of 75.0 kg, are connected by a 10.0-m rope of negligible mass. They are isolated in space, orbiting their center of mass at speeds of 5.00 m/s. Treating the astronauts as particles, calculate (a) the magnitude of the angular momentum of the two-astronaut system and (b) the rotational energy of the system. By pulling on the rope, one astronaut shortens the distance between them to 5.00 m. (c) What is the new angular momentum of the system? (d) What are the astronauts new speeds? (e) What is the new rotational energy of the system? (f) How much chemical potential energy in the body of the astronaut was converted to mechanical energy in the system when he shortened the rope? Figure P10.67 Problems 67 and 68.arrow_forwardA student sits on a freely rotating stool holding two dumbbells, each of mass 3.00 kg (Fig. P10.56). When his arms are extended horizontally (Fig. P10.56a), the dumbbells are 1.00 m from the axis of rotation and the student rotates with an angular speed of 0.750 rad/s. The moment of inertia of the student plus stool is 3.00 kg m2 and is assumed to be constant. The student pulls the dumbbells inward horizontally to a position 0.300 m from the rotation axis (Fig. P10.56b). (a) Find the new angular speed of the student. (b) Find the kinetic energy of the rotating system before and after he pulls the dumbbells inward. Figure P10.56arrow_forward
- A long, uniform rod of length L and mass M is pivoted about a frictionless, horizontal pin through one end. The rod is released from rest in a vertical position as shown in Figure P10.65. At the instant the rod is horizontal, find (a) its angular speed, (b) the magnitude of its angular acceleration, (c) the x and y components of the acceleration of its center of mass, and (d) the components of the reaction force at the pivot. Figure P10.65arrow_forwardThe velocity of a particle of mass m = 2.00 kg is given by v= 5.10 + 2.40 m /s. What is the angular momentumof the particle around the origin when it is located atr= 8.60 3.70 m?arrow_forwardA buzzard (m = 9.29 kg) is flying in circular motion with aspeed of 8.44 m/s while viewing its meal below. If the radius ofthe buzzards circular motion is 8.00 m, what is the angularmomentum of the buzzardaround the center of its motion?arrow_forward
- Rigid rods of negligible mass lying along the y axis connect three particles (Fig. P10.18). The system rotates about the x axis with an angular speed of 2.00 rad/s. Find (a) the moment of inertia about the x axis, (b) the total rotational kinetic energy evaluated from 12I2, (c) the tangential speed of each particle, and (d) the total kinetic energy evaluated from 12mivi2. (e) Compare the answers for kinetic energy in parts (b) and (d). Figure P10.18arrow_forwardA horizontal disk with moment of inertia I1 rotates with angular speed 1 about a vertical frictionless axle. A second horizontal disk having moment of inertia I2 drops onto the first, initially not rotating but sharing the same axis as the first disk. Because their surfaces are rough, the two disks eventually reach the same angular speed . The ratio /l is equal to (a) I1/I2 (b) I2/I1 (c) I1/( I1 + I2) (d) I2/( I1 + I2)arrow_forwardA long, thin rod of mass m = 5.00 kg and length = 1.20 m rotates around an axis perpendicular to the rod with an angularspeed of 3.00 rad/s. a. What is the angular momentum of therod if the axis passes through the rods midpoint? b. What is theangular momentum of the rod if the axis passes through a pointhalfway between its midpoint and its end?arrow_forward
- Figure OQ10.6 shows a system of four particles joined by light, rigid rods. Assume a = b and M is larger than m. About which of the coordinate axes does the system have (i) the smallest and (ii) the largest moment of inertia? (a) the x axis (b) the y axis (c) the z axis, (d) The moment of inertia is the same small value for two axes, (e) The moment of inertia is the same for all three axes.arrow_forwardA playground merry-go-round of radius R = 2.00 m has a moment of inertia I = 250 kg m2 and is rotating at 10.0 rev/min about a frictionless, vertical axle. Facing the axle, a 25.0-kg child hops onto the merry-go-round and manages to sit down on the edge. What is the new angular speed of the merry-go-round?arrow_forwardA rigid, massless rod has three particles with equal masses attached to it as shown in Figure P11.37. The rod is free to rotate in a vertical plane about a frictionless axle perpendicular to the rod through the point P and is released from rest in the horizontal position at t = 0. Assuming m and d are known, find (a) the moment of inertia of the system of three particles about the pivot, (b) the torque acting on the system at t = 0, (c) the angular acceleration of the system at t = 0, (d) the linear acceleration of the particle labeled 3 at t = 0, (e) the maximum kinetic energy of the system, (f) the maximum angular speed reached by the rod, (g) the maximum angular momentum of the system, and (h) the maximum speed reached by the particle labeled 2. Figure P11.37arrow_forward
 Principles of Physics: A Calculus-Based TextPhysicsISBN:9781133104261Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning
Principles of Physics: A Calculus-Based TextPhysicsISBN:9781133104261Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning College PhysicsPhysicsISBN:9781285737027Author:Raymond A. Serway, Chris VuillePublisher:Cengage Learning
College PhysicsPhysicsISBN:9781285737027Author:Raymond A. Serway, Chris VuillePublisher:Cengage Learning University Physics Volume 1PhysicsISBN:9781938168277Author:William Moebs, Samuel J. Ling, Jeff SannyPublisher:OpenStax - Rice University
University Physics Volume 1PhysicsISBN:9781938168277Author:William Moebs, Samuel J. Ling, Jeff SannyPublisher:OpenStax - Rice University Physics for Scientists and EngineersPhysicsISBN:9781337553278Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning
Physics for Scientists and EngineersPhysicsISBN:9781337553278Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning Physics for Scientists and Engineers with Modern ...PhysicsISBN:9781337553292Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning
Physics for Scientists and Engineers with Modern ...PhysicsISBN:9781337553292Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning College PhysicsPhysicsISBN:9781305952300Author:Raymond A. Serway, Chris VuillePublisher:Cengage Learning
College PhysicsPhysicsISBN:9781305952300Author:Raymond A. Serway, Chris VuillePublisher:Cengage Learning





