
Concept explainers
When a person stands on tiptoe (a strenuous position), the position of the foot is as shown in Figure P8.24a. The total gravitational force on the body,
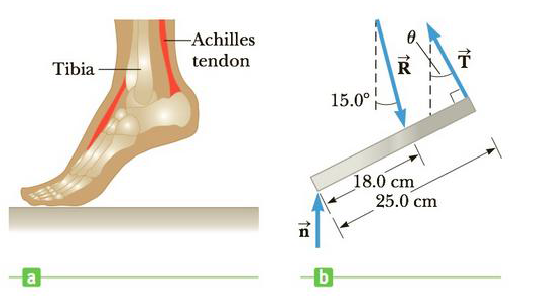
Figure P8.24
Trending nowThis is a popular solution!

Chapter 8 Solutions
College Physics
Additional Science Textbook Solutions
An Introduction to Thermal Physics
Fundamentals of Physics Extended
Essential University Physics (3rd Edition)
The Cosmic Perspective
Tutorials in Introductory Physics
- BIO The arm in Figure P10.35 weighs 41.5 N. The gravitational force on the arm acts through point A. Determine the magnitudes of the tension force F1 in the deltoid muscle and the force Fs exerted by the shoulder on the humerus (upper-arm bone) to hold the arm in the position shown. Figure P10.35arrow_forwardA spherical shell rolls without slipping down a slope which makes an angle of 30° with the horizontal (the coefficients of friction between the shell and slope are μs = 0.5 and μk = 0.3). What is the acceleration of its center of mass? A) 2.35 m/s2 B) 7.35 m/s2 C) 2.45 m/s2 D) 2.94 m/s2 E) 4.90 m/s2arrow_forwardChildren playing pirates have suspended a uniform wooden plank with mass 15.0 kg and length 2.50 m as shown in Figure P14.27. What is the tension in each of the three ropes when Sophia, with a mass of 23.0 kg, is made to walk the plank and is 1.50 m from reaching the end of the plank? FIGURE P14.27arrow_forward
- As shown in Figure OQ10.9, a cord is wrapped onto a cylindrical reel mounted on a fixed, frictionless, horizontal axle. When does the reel have a greater magnitude of angular acceleration? (a) When the cord is pulled down with a constant force of 50 N. (b) When an object of weight 50 N is hung from the cord and released. (c) The angular accelerations in parts (a) and (b) are equal. (d) It is impossible to determine. Figure OQ10.9arrow_forwardThe Iron Cross When a gymnast weighing 750 N executes the iron cross as in Figure lN.91a, the primary muscles involved in supporting this position are the latissimus dorsi (lats") and the pectoralis major (pecs"). The rings exert an upward force on the aims and support the weight of the gymnast. The force exerted by the shoulder joint on the arm is labeled Fs, while the two muscles exert a total force Fw on the arm. Estimate the magnitude of the force Fw. Note that one ring supports half the weight of the gymnast, which is 375 N as indicated in Figure P8.91b. Assume that the force Fw acts at an angle of 45 below the horizontal at a distance of 4.0 cm from the shoulder joint In your estimate, take the distance from the shoulder joint to the hand to be L = 70 cm and ignore the weight of the arm.arrow_forwardFigure P10.82 shows a vertical force applied tangentially to a uniform cylinder of weight Fg. The coefficient of static friction between the cylinder and all surfaces is 0.500. The force P is increased in magnitude until the cylinder begins to rotate. In terms of Fg, find the maximum force magnitude P that can be applied without causing the cylinder to rotate. Suggestion: Show that both friction forces will be at their maximum values when the cylinder is on the verge of slipping. Figure P10.82arrow_forward
- A long, uniform rod of length L and mass M is pivoted about a frictionless, horizontal pin through one end. The rod is released from rest in a vertical position as shown in Figure P10.65. At the instant the rod is horizontal, find (a) its angular speed, (b) the magnitude of its angular acceleration, (c) the x and y components of the acceleration of its center of mass, and (d) the components of the reaction force at the pivot. Figure P10.65arrow_forwardReview. A block of mass m1 = 2.00 kg and a block of mass m2 = 6.00 kg are connected by a massless string over a pulley in the shape of a solid disk having radius R = 0.250 m and mass M = 10.0 kg. The fixed, wedge-shaped ramp makes an angle of = 30.0 as shown in Figure P10.16. The coefficient of kinetic friction is 0.360 for both blocks. (a) Draw force diagrams of both blocks and of the pulley. Determine (b) the acceleration of the two blocks and (c) the tensions in the string on both sides of the pulley. Figure P10.16arrow_forwardA particle of mass m moves along a straight line with constant velocity v0 in the x direction, a distance b from the x axis (Fig. P13.10). (a) Does the particle possess any angular momentum about the origin? (b) Explain why the amount of its angular momentum should change or should stay constant. (c) Show that Keplers second law is satisfied by showing that the two shaded triangles in the figure have the same area when . Figure P13.10arrow_forward
- Why is the following situation impossible? A mischievous child goes to an amusement park with his family. On one ride, after a severe scolding from his mother, he slips out of his seat and climbs to the top of the rides structure, which is shaped like a cone with its axis vertical and its sloped sides making an angle of = 20.0 with the horizontal as shown in Figure P6.32. This part of the structure rotates about the vertical central axis when the ride operates. The child sits on the sloped surface at a point d = 5.32 m down the sloped side from the center of the cone and pouts. The coefficient of static friction between the boy and the cone is 0.700. The ride operator does not notice that the child has slipped away from his seat and so continues to operate the ride. As a result, the sitting, pouting boy rotates in a circular path at a speed of 3.75 m/s. Figure P6.32arrow_forwardThe puck in Figure P11.46 has a mass of 0.120 kg. The distance of the puck from the center of rotation is originally 40.0 cm, and the puck is sliding with a speed of 80.0 cm/s. The string is pulled downward 15.0 cm through the hole in the frictionless table. Determine the work done on the puck. (Suggestion: Consider the change of kinetic energy.) Figure P11.46arrow_forward
 College PhysicsPhysicsISBN:9781305952300Author:Raymond A. Serway, Chris VuillePublisher:Cengage Learning
College PhysicsPhysicsISBN:9781305952300Author:Raymond A. Serway, Chris VuillePublisher:Cengage Learning College PhysicsPhysicsISBN:9781285737027Author:Raymond A. Serway, Chris VuillePublisher:Cengage Learning
College PhysicsPhysicsISBN:9781285737027Author:Raymond A. Serway, Chris VuillePublisher:Cengage Learning Principles of Physics: A Calculus-Based TextPhysicsISBN:9781133104261Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning
Principles of Physics: A Calculus-Based TextPhysicsISBN:9781133104261Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning Physics for Scientists and Engineers, Technology ...PhysicsISBN:9781305116399Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning
Physics for Scientists and Engineers, Technology ...PhysicsISBN:9781305116399Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning Physics for Scientists and Engineers with Modern ...PhysicsISBN:9781337553292Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning
Physics for Scientists and Engineers with Modern ...PhysicsISBN:9781337553292Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning Physics for Scientists and EngineersPhysicsISBN:9781337553278Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning
Physics for Scientists and EngineersPhysicsISBN:9781337553278Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning





