
Chemistry
10th Edition
ISBN: 9781305957404
Author: Steven S. Zumdahl, Susan A. Zumdahl, Donald J. DeCoste
Publisher: Cengage Learning
expand_more
expand_more
format_list_bulleted
Concept explainers
Textbook Question
Chapter 10, Problem 87E
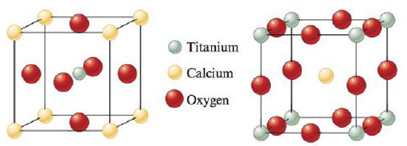
Perovskite is a mineral containing calcium, titanium, and oxygen. Two different representations of the unit cell are shown below. Show that both these representations give the same formula and the same number of oxygen atoms around each titanium atom.
Expert Solution & Answer
Trending nowThis is a popular solution!

Chapter 10 Solutions
Chemistry
Ch. 10 - What are intermolecular forces? How do they differ...Ch. 10 - Define the following terms and describe how each...Ch. 10 - Compare and contrast solids, liquids, and gases.Ch. 10 - Prob. 4RQCh. 10 - What is a lattice? What is a unit cell? Describe a...Ch. 10 - What is closest packing? What is the difference...Ch. 10 - Describe, in general, the structures of ionic...Ch. 10 - Prob. 9RQCh. 10 - Prob. 10RQCh. 10 - Compare and contrast the phase diagrams of water...
Ch. 10 - It is possible to balance a paper clip on the...Ch. 10 - Consider a sealed container half-filled with...Ch. 10 - Explain the following: You add 100 mL water to a...Ch. 10 - Prob. 4ALQCh. 10 - Prob. 5ALQCh. 10 - Why do liquids have a vapor pressure? Do all...Ch. 10 - Prob. 7ALQCh. 10 - What is the vapor pressure of water at 100C? How...Ch. 10 - Prob. 9ALQCh. 10 - Prob. 10ALQCh. 10 - Prob. 11ALQCh. 10 - Why is N2 a gas at room temperature? Explain why...Ch. 10 - Prob. 13ALQCh. 10 - In the diagram below, which lines represent the...Ch. 10 - Prob. 16QCh. 10 - Prob. 17QCh. 10 - The conductivity of silicon is enhanced by doping....Ch. 10 - Atoms are assumed to touch in closest packed...Ch. 10 - Define critical temperature and critical pressure....Ch. 10 - Prob. 21QCh. 10 - Describe what is meant by a dynamic equilibrium in...Ch. 10 - Prob. 23QCh. 10 - Prob. 24QCh. 10 - Prob. 25QCh. 10 - Prob. 26QCh. 10 - When wet laundry is hung on a clothesline on a...Ch. 10 - You have three covalent compounds with three very...Ch. 10 - Prob. 30QCh. 10 - Compare and contrast the structures of the...Ch. 10 - Silicon carbide (SiC) is an extremely hard...Ch. 10 - A common prank on college campuses is to switch...Ch. 10 - A plot of In (Pvap) versus 1/T (K) is linear with...Ch. 10 - Prob. 36QCh. 10 - Identify the most important types of interparticle...Ch. 10 - Prob. 38ECh. 10 - Predict which substance in each of the following...Ch. 10 - Consider the compounds CI2, HCI. F2, NaF, and HF....Ch. 10 - Prob. 41ECh. 10 - Consider the following electrostatic potential...Ch. 10 - In each of the following groups of substances,...Ch. 10 - Prob. 44ECh. 10 - The shape of the meniscus of water in a glass tube...Ch. 10 - Prob. 46ECh. 10 - Hydrogen peroxide (H2O2) is a syrupy liquid with a...Ch. 10 - Carbon diselenide (CSe2) is a liquid at room...Ch. 10 - X rays from a copper X-ray tube ( = 154 pm) were...Ch. 10 - The second-order diffraction (n = 2) for a gold...Ch. 10 - A topaz crystal has an interplanar spacing (d) of...Ch. 10 - X rays of wavelength 2.63 were used to analyze a...Ch. 10 - Calcium has a cubic closest packed structure as a...Ch. 10 - Nickel has a face-centered cubic unit cell. The...Ch. 10 - A certain form of lead has a cubic closest packed...Ch. 10 - The density of polonium metal is 9.2 g/cm3. If the...Ch. 10 - You are given a small bar of an unknown metal X....Ch. 10 - A metallic solid with atoms in a face-centered...Ch. 10 - Titanium metal has a body-centered cubic unit...Ch. 10 - Barium has a body-centered cubic structure. If the...Ch. 10 - The radius of gold is 144 pm, and the density is...Ch. 10 - The radius of tungsten is 137 pm and the density...Ch. 10 - What fraction of the total volume of a cubic...Ch. 10 - Iron has a density of 7.86 g/cm3 and crystallizes...Ch. 10 - Prob. 65ECh. 10 - Prob. 66ECh. 10 - Selenium is a semiconductor used in photocopying...Ch. 10 - Prob. 68ECh. 10 - Prob. 69ECh. 10 - Prob. 70ECh. 10 - The structures of some common crystalline...Ch. 10 - The unit cell for nickel arsenide is shown below....Ch. 10 - Cobalt fluoride crystallizes in a closest packed...Ch. 10 - The compounds Na2O, CdS, and ZrI4. all can be...Ch. 10 - What is the formula for the compound that...Ch. 10 - Prob. 76ECh. 10 - A certain metal fluoride crystallizes in such a...Ch. 10 - The structure of manganese fluoride can be...Ch. 10 - The unit cell of MgO is shown below l Does MgO...Ch. 10 - In solid KCl the smallest distance between the...Ch. 10 - The CsCl structure is a simple cubic array of...Ch. 10 - MnO has either the NaCI type structure or the CsCI...Ch. 10 - What type of solid will each of the following...Ch. 10 - What type of solid will each of the following...Ch. 10 - The memory metal, nitinol, is an alloy of nickel...Ch. 10 - Superalloys have been made of nickel and aluminum....Ch. 10 - Perovskite is a mineral containing calcium,...Ch. 10 - A mineral crystallizes in a cubic closest packed...Ch. 10 - Materials containing the elements Y, Ba, Cu, and O...Ch. 10 - The structures of another class of ceramic,...Ch. 10 - Plot the following data and determine Hvap for...Ch. 10 - From the following data for liquid nitric acid,...Ch. 10 - In Breckenridge, Colorado, the typical atmospheric...Ch. 10 - The temperature inside a pressure cooker is 115C....Ch. 10 - Diethyl ether (CH3CH2OCH2CH3) was one of the first...Ch. 10 - Mercury is the only metal that is a liquid at room...Ch. 10 - A substance, X, has the following properties:...Ch. 10 - Use the heating-cooling curve below to answer the...Ch. 10 - The molar heat of fusion of sodium metal is 2.60...Ch. 10 - Prob. 100ECh. 10 - What quantity of energy does it take to convert...Ch. 10 - An ice cube tray contains enough water at 22.0C to...Ch. 10 - A 0.250-g chunk of sodium metal is cautiously...Ch. 10 - Prob. 105ECh. 10 - Prob. 106ECh. 10 - Prob. 107ECh. 10 - Prob. 108ECh. 10 - Prob. 109ECh. 10 - Consider the following data for xenon: Triple...Ch. 10 - Prob. 111AECh. 10 - Consider the following formulas for n-pentane and...Ch. 10 - Some of the physical properties of H2O and D2O are...Ch. 10 - Rationalize the following boiling points:Ch. 10 - Consider the following vapor pressure versus...Ch. 10 - Consider the following enthalpy changes:...Ch. 10 - Consider the following data for an unknown...Ch. 10 - Consider the data for substance X given in...Ch. 10 - Prob. 119AECh. 10 - Boron nitride (BN) exists in two forms. The first...Ch. 10 - Prob. 121AECh. 10 - Argon has a cubic closest packed structure as a...Ch. 10 - Prob. 123AECh. 10 - A 20.0-g sample of ice at 10.0C is mixed with...Ch. 10 - Prob. 125AECh. 10 - Carbon tetrachloride. CCl4, has a vapor pressure...Ch. 10 - A special vessel (see Fig. 10.45) contains ice and...Ch. 10 - Prob. 128AECh. 10 - In regions with dry climates, evaporative coolers...Ch. 10 - Which of the following compound(s) exhibit only...Ch. 10 - Which of the following statements about...Ch. 10 - Prob. 133CWPCh. 10 - Aluminum has an atomic radius of 143 pm and forms...Ch. 10 - Pyrolusite is a mineral containing manganese ions...Ch. 10 - The structure of the compound K2O is best...Ch. 10 - Prob. 137CWPCh. 10 - Some ice cubes at 0c with a total mass of 403 g...Ch. 10 - The enthalpy of vaporization for acetone is 32.0...Ch. 10 - Prob. 140CWPCh. 10 - When I mole of benzene is vaporized at a constant...Ch. 10 - You and a friend each synthesize a compound with...Ch. 10 - Prob. 143CPCh. 10 - Prob. 144CPCh. 10 - Consider two different organic compounds, each...Ch. 10 - Rationalize the differences in physical properties...Ch. 10 - Prob. 147CPCh. 10 - Some ionic compounds contain a mixture of...Ch. 10 - Some ionic compounds contain a mixture of...Ch. 10 - Spinel is a mineral that contains 37.9% aluminum,...Ch. 10 - Mn crystallizes in the same type of cubic unit...Ch. 10 - You are asked to help set up a historical display...Ch. 10 - Some water is placed in a sealed glass container...Ch. 10 - The molar enthalpy of vaporization of water at 373...Ch. 10 - Prob. 155CPCh. 10 - Rubidium chloride has the sodium chloride...Ch. 10 - Prob. 157IPCh. 10 - A metal burns in air at 600c under high pressure...Ch. 10 - Prob. 159IPCh. 10 - General Zod has sold Lex Luthor what Zod claims to...
Knowledge Booster
Learn more about
Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, chemistry and related others by exploring similar questions and additional content below.Similar questions
- The CsCl structure is a simple cubic array of chloride ions with a cesium ion at the center of each cubic array (see Exercise 69). Given that the density of cesium chloride is 3.97 g/cm3, and assuming that the chloride and cesium ions touch along the body diagonal of the cubic unit cell, calculate the distance between the centers of adjacent Cs+ and Cl ions in the solid. Compare this value with the expected distance based on the sizes of the ions. The ionic radius of Cs+ is 169 pm, and the ionic radius of Cl is 181 pm.arrow_forwardSpinel is a mineral that contains 37.9% aluminum, 17.1% magnesium, and 45.0% oxygen, by mass, and has a density of 3.57 g/cm3.The edge of the cubic unit cell measures 809 pm. How many of each type of ion are present in the unit cell?arrow_forwardCalculate the percent of volume that is actually occupied by spheres in a face-centered cubic lattice of identical spheres. You can do this by first relating the radius of a sphere, r, to the length of an edge of a unit cell, l. (Note that the spheres do not touch along an edge but do touch along the diagonal of a face.) Then calculate the volume of a unit cell in terms of r. The volume occupied by spheres equals the number of spheres per unit cell times the volume of a sphere (4r3/3).arrow_forward
arrow_back_ios
arrow_forward_ios
Recommended textbooks for you
 ChemistryChemistryISBN:9781305957404Author:Steven S. Zumdahl, Susan A. Zumdahl, Donald J. DeCostePublisher:Cengage Learning
ChemistryChemistryISBN:9781305957404Author:Steven S. Zumdahl, Susan A. Zumdahl, Donald J. DeCostePublisher:Cengage Learning
 Chemistry: An Atoms First ApproachChemistryISBN:9781305079243Author:Steven S. Zumdahl, Susan A. ZumdahlPublisher:Cengage Learning
Chemistry: An Atoms First ApproachChemistryISBN:9781305079243Author:Steven S. Zumdahl, Susan A. ZumdahlPublisher:Cengage Learning Chemistry: Principles and PracticeChemistryISBN:9780534420123Author:Daniel L. Reger, Scott R. Goode, David W. Ball, Edward MercerPublisher:Cengage Learning
Chemistry: Principles and PracticeChemistryISBN:9780534420123Author:Daniel L. Reger, Scott R. Goode, David W. Ball, Edward MercerPublisher:Cengage Learning Chemistry & Chemical ReactivityChemistryISBN:9781337399074Author:John C. Kotz, Paul M. Treichel, John Townsend, David TreichelPublisher:Cengage Learning
Chemistry & Chemical ReactivityChemistryISBN:9781337399074Author:John C. Kotz, Paul M. Treichel, John Townsend, David TreichelPublisher:Cengage Learning Chemistry: The Molecular ScienceChemistryISBN:9781285199047Author:John W. Moore, Conrad L. StanitskiPublisher:Cengage Learning
Chemistry: The Molecular ScienceChemistryISBN:9781285199047Author:John W. Moore, Conrad L. StanitskiPublisher:Cengage Learning

Chemistry
Chemistry
ISBN:9781305957404
Author:Steven S. Zumdahl, Susan A. Zumdahl, Donald J. DeCoste
Publisher:Cengage Learning


Chemistry: An Atoms First Approach
Chemistry
ISBN:9781305079243
Author:Steven S. Zumdahl, Susan A. Zumdahl
Publisher:Cengage Learning

Chemistry: Principles and Practice
Chemistry
ISBN:9780534420123
Author:Daniel L. Reger, Scott R. Goode, David W. Ball, Edward Mercer
Publisher:Cengage Learning

Chemistry & Chemical Reactivity
Chemistry
ISBN:9781337399074
Author:John C. Kotz, Paul M. Treichel, John Townsend, David Treichel
Publisher:Cengage Learning

Chemistry: The Molecular Science
Chemistry
ISBN:9781285199047
Author:John W. Moore, Conrad L. Stanitski
Publisher:Cengage Learning
Unit Cell Chemistry Simple Cubic, Body Centered Cubic, Face Centered Cubic Crystal Lattice Structu; Author: The Organic Chemistry Tutor;https://www.youtube.com/watch?v=HCWwRh5CXYU;License: Standard YouTube License, CC-BY