Chapter 4, Problem 20RE

(a)

To determine

To graph:the given function $\mathrm{f}$ to estimate the maximum and minimum values.

Explanation of Solution

Given:

The function is

  $\mathrm{f}\left(\mathrm{x}\right)=\frac{1}{1+{\mathrm{e}}^{\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$\mathrm{x}$}\right.}}$

Concept used:

The slope of the tangent to a curve $\mathrm{f}\left(\mathrm{x}\right)$ at any point a is given by the value of the first derivative of the slope at the point $\mathrm{x}=\mathrm{a}$ .

The tangent to be horizontal so the slope should be equal to 0

That is $\frac{\mathrm{d}\mathrm{y}}{\mathrm{d}\mathrm{x}}=0$ .

Calculation:

The function is

  $\mathrm{f}\left(\mathrm{x}\right)=\frac{1}{1+{\mathrm{e}}^{\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$\mathrm{x}$}\right.}}\mathrm{................................}\left(1\right)$

Draw the table

  $\mathrm{f}\left(\mathrm{x}\right)=\frac{1}{1+{\mathrm{e}}^{\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$\mathrm{x}$}\right.}}$

Test one point in each of the region formed by the graph

If the point satisfies the function then shade the entire region to denote that every point in the region satisfies the function

$\mathrm{x}-\mathrm{a}\mathrm{x}\mathrm{i}\mathrm{s}$	$0$	$0$	$2$	$3$
$\mathrm{y}-\mathrm{a}\mathrm{x}\mathrm{i}\mathrm{s}$	$0$	$1$	$0.36$	$0.39$

Draw the graph

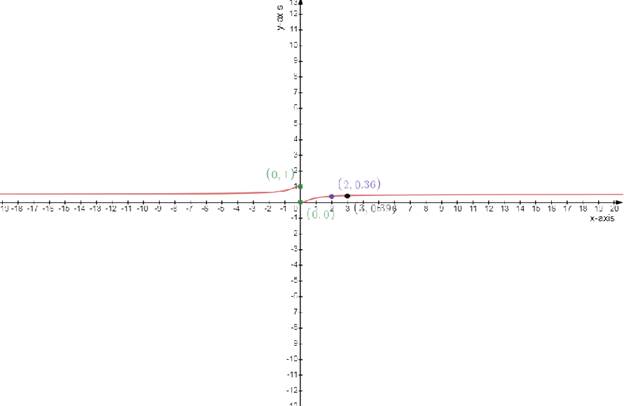
  $\mathrm{f}\left(\mathrm{x}\right)=\frac{1}{1+{\mathrm{e}}^{\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$\mathrm{x}$}\right.}}$

  

(b)

To determine

To find: The graph of $\mathrm{f}$ has a vertical tangent or a vertical cusp at c .

Answer to Problem 20RE

  $\mathrm{f}\text{'}\left(0\right)=\mathrm{\infty }$

Explanation of Solution

Given:

The function $\mathrm{f}\left(\mathrm{x}\right)=\frac{1}{1+{\mathrm{e}}^{\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$\mathrm{x}$}\right.}}$

Concept used:

The definition of a vertical cusp is that the one sided limits of the derivative approach opposite $\pm \mathrm{\infty }$

: positive infinity on one side and negative infinity on the other side . A vertical tangent has the one sided limits of the derivative equal to the same sign of infinity

The derivative at the relevant point is undefined in both the cusp and the vertical tangent

Calculation:

The function is $\mathrm{f}\left(\mathrm{x}\right)=\frac{1}{1+{\mathrm{e}}^{\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$\mathrm{x}$}\right.}}\mathrm{.........}\left(1\right)$

Differentiating equation (1) with respect to $\mathrm{x}$

  $\begin{array}{l}\mathrm{f}\left(\mathrm{x}\right)=\frac{1}{1+{\mathrm{e}}^{\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$\mathrm{x}$}\right.}}\\ {\mathrm{f}}^{\prime }\left(\mathrm{x}\right)=-\frac{{\mathrm{e}}^{\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$\mathrm{x}$}\right.}}{{\mathrm{x}}^2{\left(1+{\mathrm{e}}^{\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$\mathrm{x}$}\right.}\right)}^2}\end{array}$

  ${\mathrm{f}}^{\prime }\left(\mathrm{x}\right)$ is the maximum value

(c)

To determine

To find:

The maximum and minimum values and the exact values.

Answer to Problem 20RE

  $\mathrm{f}\text{'}\left(0\right)=\mathrm{\infty }$

Explanation of Solution

Given:

The function $\mathrm{f}\left(\mathrm{x}\right)=\frac{1}{1+{\mathrm{e}}^{\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$\mathrm{x}$}\right.}}$

Concept used:

The definition of a vertical cusp is that the one sided limits of the derivative approach opposite $\pm \mathrm{\infty }$

: positive infinity on one side and negative infinity on the other side . A vertical tangent has the one sided limits of the derivative equal to the same sign of infinity

The derivative at the relevant point is undefined in both the cusp and the vertical tangent

Calculation:

The function is $\mathrm{f}\left(\mathrm{x}\right)=\frac{1}{1+{\mathrm{e}}^{\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$\mathrm{x}$}\right.}}\mathrm{.........}\left(1\right)$

Differentiating equation (1) with respect to $\mathrm{x}$

  $\begin{array}{l}\mathrm{f}\left(\mathrm{x}\right)=\frac{1}{1+{\mathrm{e}}^{\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$\mathrm{x}$}\right.}}\\ {\mathrm{f}}^{\prime }\left(\mathrm{x}\right)=-\frac{{\mathrm{e}}^{\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$\mathrm{x}$}\right.}}{{\mathrm{x}}^2{\left(1+{\mathrm{e}}^{\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$\mathrm{x}$}\right.}\right)}^2}\end{array}$

  ${\mathrm{f}}^{\prime }\left(\mathrm{x}\right)$ is the maximum value

  $\mathrm{f}\text{'}\left(0\right)=\mathrm{\infty }$

The vertical tangent means that the derivative at that point approaches infinity

Since the slope is infinitely large

(d)

To determine

To find:

The maximum and minimum values and the exact values.

Answer to Problem 20RE

  $\mathrm{f}\text{'}\left(0\right)=\mathrm{\infty }$

Explanation of Solution

Given:

The function $\mathrm{f}\left(\mathrm{x}\right)=\frac{1}{1+{\mathrm{e}}^{\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$\mathrm{x}$}\right.}}$

Concept used:

The definition of a vertical cusp is that the one sided limits of the derivative approach opposite $\pm \mathrm{\infty }$

: positive infinity on one side and negative infinity on the other side . A vertical tangent has the one sided limits of the derivative equal to the same sign of infinity

The derivative at the relevant point is undefined in both the cusp and the vertical tangent

Calculation:

The function is $\mathrm{f}\left(\mathrm{x}\right)=\frac{1}{1+{\mathrm{e}}^{\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$\mathrm{x}$}\right.}}\mathrm{.........}\left(1\right)$

Differentiating equation (1) with respect to $\mathrm{x}$

  $\begin{array}{l}\mathrm{f}\left(\mathrm{x}\right)=\frac{1}{1+{\mathrm{e}}^{\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$\mathrm{x}$}\right.}}\\ {\mathrm{f}}^{\prime }\left(\mathrm{x}\right)=-\frac{{\mathrm{e}}^{\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$\mathrm{x}$}\right.}}{{\mathrm{x}}^2{\left(1+{\mathrm{e}}^{\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$\mathrm{x}$}\right.}\right)}^2}\mathrm{................................}\left(2\right)\end{array}$

  ${\mathrm{f}}^{\prime }\left(\mathrm{x}\right)$ is the maximum value Again differentiating equation (2) with respect to $\mathrm{x}$

  $\begin{array}{l}{\mathrm{f}}^{\prime }=-\frac{{\mathrm{e}}^{\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$\mathrm{x}$}\right.}}{{\mathrm{x}}^2{\left(1+{\mathrm{e}}^{\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$\mathrm{x}$}\right.}\right)}^2}\\ {\mathrm{f}}^{″}=-\frac{{\left({\mathrm{e}}^{\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$\mathrm{x}$}\right.}\right)}^2}{{\mathrm{x}}^4{\left(1+{\mathrm{e}}^{\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$\mathrm{x}$}\right.}\right)}^3}\end{array}$

  ${\mathrm{f}}^{″}\left(\mathrm{x}\right)$ is the maximum value

  ${\mathrm{f}}^{″}\left(0\right)=\mathrm{\infty }$

The vertical tangent means that the derivative at that point approaches infinity

Since the slope is infinitely large

(e)

To determine

To find:

The maximum and minimum values and the exact values.

Answer to Problem 20RE

  ${\mathrm{f}}^{″}\left(0\right)=\mathrm{\infty }$

Explanation of Solution

Given:

The function $\mathrm{f}\left(\mathrm{x}\right)=\frac{1}{1+{\mathrm{e}}^{\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$\mathrm{x}$}\right.}}$

Concept used:

The definition of a vertical cusp is that the one sided limits of the derivative approach opposite $\pm \mathrm{\infty }$

: positive infinity on one side and negative infinity on the other side . A vertical tangent has the one sided limits of the derivative equal to the same sign of infinity

The derivative at the relevant point is undefined in both the cusp and the vertical tangent

Calculation:

The function is $\mathrm{f}\left(\mathrm{x}\right)=\frac{1}{1+{\mathrm{e}}^{\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$\mathrm{x}$}\right.}}\mathrm{.........}\left(1\right)$

Differentiating equation (1) with respect to $\mathrm{x}$

  $\begin{array}{l}\mathrm{f}\left(\mathrm{x}\right)=\frac{1}{1+{\mathrm{e}}^{\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$\mathrm{x}$}\right.}}\\ {\mathrm{f}}^{″}=-\frac{{\left({\mathrm{e}}^{\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$\mathrm{x}$}\right.}\right)}^2}{{\mathrm{x}}^4{\left(1+{\mathrm{e}}^{\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$\mathrm{x}$}\right.}\right)}^3}\\ 0=-\frac{{\left({\mathrm{e}}^{\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$\mathrm{x}$}\right.}\right)}^2}{{\mathrm{x}}^4{\left(1+{\mathrm{e}}^{\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$\mathrm{x}$}\right.}\right)}^3}\\ {\left({\mathrm{e}}^{\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$\mathrm{x}$}\right.}\right)}^2=\mathrm{0.............................}\left(2\right)\end{array}$

  ${\mathrm{f}}^{″}\left(0\right)=\mathrm{\infty }$

The vertical tangent means that the derivative at that point approaches infinity

Since the slope is infinitely large