
Concept explainers
(a)
To state: The Rolle ’s Theorem.
(a)
Explanation of Solution
The Rolle’s theorem states that, “if function f satisfies the following three hypotheses,
(1) Function f is continuous on
(2) Function f is differentiable on
(3)
Then, there is a number c in
(b)
To state: The mean value theorem and interpret its geometrical meaning.
(b)
Explanation of Solution
The mean value theorem states that, “if a function f satisfies the following hypotheses,
(1)Function f is continuous on
(2) Function f is differentiable on
Then, there is a number c in
Geometrically mean value theorem can be explained as follow.
The slope of the secant line joining the points
Therefore, the equation
Diagrammatic representation of the function is shown below in Figure 1.
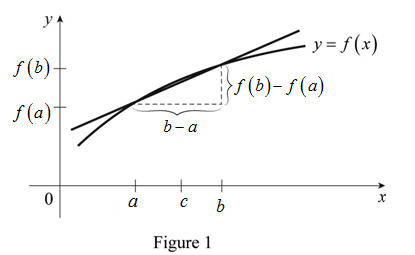
From Figure 1, it is noticed that secant line becomes tangent with slope
Chapter 4 Solutions
Single Variable Calculus: Concepts and Contexts, Enhanced Edition
 Calculus: Early TranscendentalsCalculusISBN:9781285741550Author:James StewartPublisher:Cengage Learning
Calculus: Early TranscendentalsCalculusISBN:9781285741550Author:James StewartPublisher:Cengage Learning Thomas' Calculus (14th Edition)CalculusISBN:9780134438986Author:Joel R. Hass, Christopher E. Heil, Maurice D. WeirPublisher:PEARSON
Thomas' Calculus (14th Edition)CalculusISBN:9780134438986Author:Joel R. Hass, Christopher E. Heil, Maurice D. WeirPublisher:PEARSON Calculus: Early Transcendentals (3rd Edition)CalculusISBN:9780134763644Author:William L. Briggs, Lyle Cochran, Bernard Gillett, Eric SchulzPublisher:PEARSON
Calculus: Early Transcendentals (3rd Edition)CalculusISBN:9780134763644Author:William L. Briggs, Lyle Cochran, Bernard Gillett, Eric SchulzPublisher:PEARSON Calculus: Early TranscendentalsCalculusISBN:9781319050740Author:Jon Rogawski, Colin Adams, Robert FranzosaPublisher:W. H. Freeman
Calculus: Early TranscendentalsCalculusISBN:9781319050740Author:Jon Rogawski, Colin Adams, Robert FranzosaPublisher:W. H. Freeman
 Calculus: Early Transcendental FunctionsCalculusISBN:9781337552516Author:Ron Larson, Bruce H. EdwardsPublisher:Cengage Learning
Calculus: Early Transcendental FunctionsCalculusISBN:9781337552516Author:Ron Larson, Bruce H. EdwardsPublisher:Cengage Learning





