
Single Variable Calculus: Concepts and Contexts, Enhanced Edition
4th Edition
ISBN: 9781337687805
Author: James Stewart
Publisher: Cengage Learning
expand_more
expand_more
format_list_bulleted
Concept explainers
Question
Chapter 4, Problem 19RE
To determine
To find: The inflection point for the given function.
Expert Solution & Answer
Answer to Problem 19RE
The inflection point for the given function is
Explanation of Solution
Given information:
The function is
Calculation:
Consider the equation.
The graph
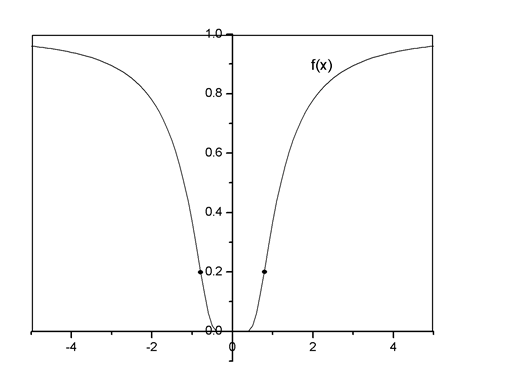
Figure-1
Differentiate above equation.
And,
Substitute
Substitute
Thus, the point of inflection is
Chapter 4 Solutions
Single Variable Calculus: Concepts and Contexts, Enhanced Edition
Ch. 4.1 - Prob. 1ECh. 4.1 - Prob. 2ECh. 4.1 - Prob. 3ECh. 4.1 - Prob. 4ECh. 4.1 - Prob. 5ECh. 4.1 - Prob. 6ECh. 4.1 - Prob. 7ECh. 4.1 - Prob. 8ECh. 4.1 - Prob. 9ECh. 4.1 - Prob. 10E
Ch. 4.1 - Prob. 11ECh. 4.1 - Prob. 12ECh. 4.1 - Prob. 13ECh. 4.1 - Prob. 14ECh. 4.1 - Prob. 15ECh. 4.1 - Prob. 16ECh. 4.1 - Prob. 17ECh. 4.1 - Prob. 18ECh. 4.1 - Prob. 19ECh. 4.1 - Prob. 20ECh. 4.1 - Prob. 21ECh. 4.1 - Prob. 22ECh. 4.1 - Prob. 23ECh. 4.1 - Prob. 24ECh. 4.1 - Prob. 25ECh. 4.1 - Prob. 26ECh. 4.1 - Prob. 27ECh. 4.1 - Prob. 28ECh. 4.1 - Prob. 29ECh. 4.1 - Prob. 30ECh. 4.1 - Prob. 31ECh. 4.1 - Prob. 32ECh. 4.1 - Prob. 33ECh. 4.1 - Prob. 34ECh. 4.1 - Prob. 35ECh. 4.1 - Prob. 36ECh. 4.1 - Prob. 37ECh. 4.1 - Prob. 38ECh. 4.1 - Prob. 39ECh. 4.1 - Prob. 40ECh. 4.1 - Prob. 41ECh. 4.1 - Prob. 42ECh. 4.1 - Prob. 43ECh. 4.1 - Prob. 44ECh. 4.2 - Explain the difference between an absolute minimum...Ch. 4.2 - Prob. 2ECh. 4.2 - Prob. 3ECh. 4.2 - For each of the numbers a, b, c, d, r, and s,...Ch. 4.2 - Prob. 5ECh. 4.2 - Use the graph to state the absolute and local...Ch. 4.2 - Prob. 7ECh. 4.2 - Prob. 8ECh. 4.2 - Prob. 9ECh. 4.2 - Prob. 10ECh. 4.2 - (a) Sketch the graph of a function that has a...Ch. 4.2 - Prob. 12ECh. 4.2 - (a) Sketch the graph of a function on [1, 2] that...Ch. 4.2 - Prob. 14ECh. 4.2 - Prob. 15ECh. 4.2 - Prob. 16ECh. 4.2 - Prob. 17ECh. 4.2 - Prob. 18ECh. 4.2 - Prob. 19ECh. 4.2 - Prob. 20ECh. 4.2 - Prob. 21ECh. 4.2 - Prob. 22ECh. 4.2 - Prob. 23ECh. 4.2 - Find the critical numbers of the function. f(x) =...Ch. 4.2 - Find the critical numbers of the function. f(x) =...Ch. 4.2 - Prob. 26ECh. 4.2 - Find the critical numbers of the function. g(t) =...Ch. 4.2 - Prob. 28ECh. 4.2 - Find the critical numbers of the function....Ch. 4.2 - Prob. 30ECh. 4.2 - Prob. 31ECh. 4.2 - Prob. 32ECh. 4.2 - Prob. 33ECh. 4.2 - Find the critical numbers of the function. g() = 4...Ch. 4.2 - Find the critical numbers of the function. f() = 2...Ch. 4.2 - Find the critical numbers of the function. h(t) =...Ch. 4.2 - Find the critical numbers of the function. f(x) =...Ch. 4.2 - Prob. 38ECh. 4.2 - Prob. 39ECh. 4.2 - A formula for the derivative of a function f is...Ch. 4.2 - Prob. 41ECh. 4.2 - Prob. 42ECh. 4.2 - Prob. 43ECh. 4.2 - Prob. 44ECh. 4.2 - Prob. 45ECh. 4.2 - Prob. 46ECh. 4.2 - Prob. 47ECh. 4.2 - Prob. 48ECh. 4.2 - Prob. 49ECh. 4.2 - Prob. 50ECh. 4.2 - Prob. 51ECh. 4.2 - Prob. 52ECh. 4.2 - Prob. 53ECh. 4.2 - Prob. 54ECh. 4.2 - Prob. 55ECh. 4.2 - Prob. 56ECh. 4.2 - Prob. 57ECh. 4.2 - Prob. 58ECh. 4.2 - Prob. 59ECh. 4.2 - Prob. 60ECh. 4.2 - Prob. 61ECh. 4.2 - Prob. 62ECh. 4.2 - Prob. 63ECh. 4.2 - Prob. 64ECh. 4.2 - Prob. 65ECh. 4.2 - Prob. 66ECh. 4.3 - Prob. 1ECh. 4.3 - Prob. 2ECh. 4.3 - Prob. 3ECh. 4.3 - Prob. 4ECh. 4.3 - Prob. 5ECh. 4.3 - Prob. 6ECh. 4.3 - Prob. 7ECh. 4.3 - Prob. 8ECh. 4.3 - Prob. 9ECh. 4.3 - Prob. 10ECh. 4.3 - Prob. 11ECh. 4.3 - Prob. 12ECh. 4.3 - Prob. 13ECh. 4.3 - Prob. 14ECh. 4.3 - Prob. 15ECh. 4.3 - Prob. 16ECh. 4.3 - Prob. 17ECh. 4.3 - Prob. 18ECh. 4.3 - Prob. 19ECh. 4.3 - Prob. 20ECh. 4.3 - Prob. 21ECh. 4.3 - Prob. 22ECh. 4.3 - Prob. 23ECh. 4.3 - Prob. 24ECh. 4.3 - Prob. 25ECh. 4.3 - Prob. 26ECh. 4.3 - Prob. 27ECh. 4.3 - Prob. 28ECh. 4.3 - Prob. 29ECh. 4.3 - Prob. 30ECh. 4.3 - Prob. 31ECh. 4.3 - Prob. 32ECh. 4.3 - Prob. 33ECh. 4.3 - Prob. 34ECh. 4.3 - Prob. 35ECh. 4.3 - Prob. 36ECh. 4.3 - Prob. 37ECh. 4.3 - Prob. 38ECh. 4.3 - Prob. 39ECh. 4.3 - Prob. 40ECh. 4.3 - Prob. 41ECh. 4.3 - Prob. 42ECh. 4.3 - Prob. 43ECh. 4.3 - Prob. 44ECh. 4.3 - Prob. 45ECh. 4.3 - Prob. 46ECh. 4.3 - Prob. 47ECh. 4.3 - Prob. 48ECh. 4.3 - Prob. 49ECh. 4.3 - Prob. 50ECh. 4.3 - Prob. 51ECh. 4.3 - Prob. 52ECh. 4.3 - Prob. 53ECh. 4.3 - Prob. 54ECh. 4.3 - Prob. 55ECh. 4.3 - Prob. 56ECh. 4.3 - Prob. 57ECh. 4.3 - Prob. 58ECh. 4.3 - Prob. 59ECh. 4.3 - Prob. 60ECh. 4.3 - Prob. 61ECh. 4.3 - Prob. 62ECh. 4.3 - Prob. 63ECh. 4.3 - Prob. 64ECh. 4.3 - Prob. 65ECh. 4.3 - Prob. 66ECh. 4.3 - Prob. 67ECh. 4.3 - Prob. 68ECh. 4.3 - Prob. 69ECh. 4.3 - Prob. 70ECh. 4.3 - Prob. 71ECh. 4.3 - Prob. 72ECh. 4.4 - Prob. 1ECh. 4.4 - Prob. 2ECh. 4.4 - Prob. 3ECh. 4.4 - Prob. 4ECh. 4.4 - Prob. 5ECh. 4.4 - Prob. 6ECh. 4.4 - Prob. 7ECh. 4.4 - Prob. 8ECh. 4.4 - Prob. 9ECh. 4.4 - Prob. 10ECh. 4.4 - Prob. 11ECh. 4.4 - Prob. 12ECh. 4.4 - Prob. 13ECh. 4.4 - Prob. 14ECh. 4.4 - Prob. 15ECh. 4.4 - Prob. 16ECh. 4.4 - Prob. 17ECh. 4.4 - Prob. 18ECh. 4.4 - Prob. 19ECh. 4.4 - Prob. 20ECh. 4.4 - Prob. 21ECh. 4.4 - Prob. 22ECh. 4.4 - Prob. 23ECh. 4.4 - Prob. 24ECh. 4.4 - Prob. 25ECh. 4.4 - Prob. 26ECh. 4.4 - Prob. 27ECh. 4.4 - Prob. 28ECh. 4.4 - Prob. 29ECh. 4.4 - Prob. 30ECh. 4.4 - Prob. 31ECh. 4.4 - Prob. 32ECh. 4.4 - Prob. 33ECh. 4.4 - Prob. 34ECh. 4.4 - Prob. 35ECh. 4.4 - Prob. 36ECh. 4.5 - Given that...Ch. 4.5 - Given that...Ch. 4.5 - Prob. 3ECh. 4.5 - Given that...Ch. 4.5 - Prob. 5ECh. 4.5 - Prob. 6ECh. 4.5 - Prob. 7ECh. 4.5 - Prob. 8ECh. 4.5 - Prob. 9ECh. 4.5 - Prob. 10ECh. 4.5 - Prob. 11ECh. 4.5 - Prob. 12ECh. 4.5 - Prob. 13ECh. 4.5 - Prob. 14ECh. 4.5 - Prob. 15ECh. 4.5 - Prob. 16ECh. 4.5 - Prob. 17ECh. 4.5 - Prob. 18ECh. 4.5 - Prob. 19ECh. 4.5 - Prob. 20ECh. 4.5 - Prob. 21ECh. 4.5 - Prob. 22ECh. 4.5 - Prob. 23ECh. 4.5 - Prob. 24ECh. 4.5 - Prob. 25ECh. 4.5 - Prob. 26ECh. 4.5 - Prob. 27ECh. 4.5 - Prob. 28ECh. 4.5 - Prob. 29ECh. 4.5 - Prob. 30ECh. 4.5 - Prob. 31ECh. 4.5 - Prob. 32ECh. 4.5 - Prob. 33ECh. 4.5 - Prob. 34ECh. 4.5 - Prob. 35ECh. 4.5 - Prob. 36ECh. 4.5 - Prob. 37ECh. 4.5 - Prob. 38ECh. 4.5 - Prob. 39ECh. 4.5 - Prob. 40ECh. 4.5 - Prob. 41ECh. 4.5 - Prob. 42ECh. 4.5 - Prob. 43ECh. 4.5 - Prob. 44ECh. 4.5 - Prob. 45ECh. 4.5 - Prob. 46ECh. 4.5 - Prob. 47ECh. 4.5 - Prob. 48ECh. 4.5 - Prob. 49ECh. 4.5 - Prob. 50ECh. 4.5 - Prob. 51ECh. 4.5 - Prob. 52ECh. 4.5 - Prob. 53ECh. 4.5 - Prob. 54ECh. 4.5 - Prob. 55ECh. 4.5 - Prob. 56ECh. 4.5 - Prob. 57ECh. 4.5 - Prob. 58ECh. 4.5 - Prob. 59ECh. 4.5 - Prob. 60ECh. 4.5 - Prob. 61ECh. 4.5 - Prob. 62ECh. 4.5 - Prob. 63ECh. 4.5 - Prob. 64ECh. 4.5 - Prob. 65ECh. 4.5 - Prob. 66ECh. 4.5 - Prob. 67ECh. 4.5 - Prob. 68ECh. 4.5 - Prob. 69ECh. 4.5 - Prob. 70ECh. 4.5 - Prob. 71ECh. 4.5 - Prob. 72ECh. 4.5 - Prob. 73ECh. 4.5 - Prob. 74ECh. 4.5 - Prob. 75ECh. 4.5 - Prob. 76ECh. 4.6 - Consider the following problem: Find two numbers...Ch. 4.6 - Find two numbers whose difference is 100 and whose...Ch. 4.6 - Find two positive numbers whose product is 100 and...Ch. 4.6 - The sum of two positive numbers is 16. What is the...Ch. 4.6 - Prob. 5ECh. 4.6 - Prob. 6ECh. 4.6 - Prob. 7ECh. 4.6 - The rate (in mg carbon/m3/h) at which...Ch. 4.6 - Consider the following problem: A farmer with 750...Ch. 4.6 - Prob. 10ECh. 4.6 - Prob. 11ECh. 4.6 - Prob. 12ECh. 4.6 - Prob. 13ECh. 4.6 - Prob. 14ECh. 4.6 - Prob. 15ECh. 4.6 - Prob. 16ECh. 4.6 - Prob. 17ECh. 4.6 - Prob. 18ECh. 4.6 - Prob. 19ECh. 4.6 - Prob. 20ECh. 4.6 - Prob. 21ECh. 4.6 - Prob. 22ECh. 4.6 - Prob. 23ECh. 4.6 - Prob. 24ECh. 4.6 - Prob. 25ECh. 4.6 - Prob. 26ECh. 4.6 - Prob. 27ECh. 4.6 - Prob. 28ECh. 4.6 - Prob. 29ECh. 4.6 - Prob. 30ECh. 4.6 - Prob. 31ECh. 4.6 - Prob. 32ECh. 4.6 - Prob. 33ECh. 4.6 - Prob. 34ECh. 4.6 - Prob. 35ECh. 4.6 - Prob. 36ECh. 4.6 - Prob. 37ECh. 4.6 - Prob. 38ECh. 4.6 - Prob. 39ECh. 4.6 - Prob. 40ECh. 4.6 - Prob. 41ECh. 4.6 - Prob. 42ECh. 4.6 - Prob. 43ECh. 4.6 - Prob. 44ECh. 4.6 - Prob. 45ECh. 4.6 - Prob. 46ECh. 4.6 - Prob. 47ECh. 4.6 - Prob. 48ECh. 4.6 - Prob. 49ECh. 4.6 - Prob. 50ECh. 4.6 - Prob. 51ECh. 4.6 - Prob. 52ECh. 4.6 - Prob. 53ECh. 4.6 - Prob. 54ECh. 4.6 - Prob. 55ECh. 4.6 - Prob. 56ECh. 4.6 - Prob. 57ECh. 4.6 - Prob. 58ECh. 4.6 - Prob. 59ECh. 4.6 - Prob. 60ECh. 4.6 - Prob. 61ECh. 4.6 - Prob. 62ECh. 4.7 - The figure shows the graph of a function f....Ch. 4.7 - Follow the instructions for Exercise 1(a) but use...Ch. 4.7 - Suppose the tangent line to the curve y = f(x) at...Ch. 4.7 - For each initial approximation, determine...Ch. 4.7 - Prob. 5ECh. 4.7 - Prob. 6ECh. 4.7 - Prob. 7ECh. 4.7 - Prob. 8ECh. 4.7 - Use Newtons method with initial approximation x1 =...Ch. 4.7 - Use Newtons method with initial approximation x1 =...Ch. 4.7 - Prob. 11ECh. 4.7 - Prob. 12ECh. 4.7 - Prob. 13ECh. 4.7 - Prob. 14ECh. 4.7 - Prob. 15ECh. 4.7 - Prob. 16ECh. 4.7 - Prob. 17ECh. 4.7 - Prob. 18ECh. 4.7 - Prob. 19ECh. 4.7 - Prob. 20ECh. 4.7 - Prob. 21ECh. 4.7 - Prob. 22ECh. 4.7 - (a) Apply Newtons method to the equation x2 a = 0...Ch. 4.7 - (a) Apply Newtons method to the equation 1/x a =...Ch. 4.7 - (a) Use Newtons method with x1 = 1 to find the...Ch. 4.7 - Explain why Newtons method fails when applied to...Ch. 4.7 - Prob. 28ECh. 4.7 - Prob. 29ECh. 4.7 - Prob. 30ECh. 4.7 - Prob. 31ECh. 4.7 - Prob. 32ECh. 4.7 - Prob. 33ECh. 4.7 - Prob. 34ECh. 4.8 - Prob. 1ECh. 4.8 - Prob. 2ECh. 4.8 - Prob. 3ECh. 4.8 - Prob. 4ECh. 4.8 - Prob. 5ECh. 4.8 - Prob. 6ECh. 4.8 - Prob. 7ECh. 4.8 - Prob. 8ECh. 4.8 - Prob. 9ECh. 4.8 - Prob. 10ECh. 4.8 - Prob. 11ECh. 4.8 - Prob. 12ECh. 4.8 - Prob. 13ECh. 4.8 - Prob. 14ECh. 4.8 - Prob. 15ECh. 4.8 - Prob. 16ECh. 4.8 - Prob. 19ECh. 4.8 - Prob. 20ECh. 4.8 - Prob. 21ECh. 4.8 - Prob. 22ECh. 4.8 - Prob. 23ECh. 4.8 - Prob. 24ECh. 4.8 - Prob. 25ECh. 4.8 - Prob. 26ECh. 4.8 - Prob. 27ECh. 4.8 - Prob. 28ECh. 4.8 - Prob. 29ECh. 4.8 - Prob. 30ECh. 4.8 - Prob. 31ECh. 4.8 - Prob. 32ECh. 4.8 - Prob. 33ECh. 4.8 - Prob. 34ECh. 4.8 - Prob. 35ECh. 4.8 - Prob. 36ECh. 4.8 - Prob. 37ECh. 4.8 - Prob. 38ECh. 4.8 - The graph of f is shown in the figure. Sketch the...Ch. 4.8 - Prob. 40ECh. 4.8 - Prob. 41ECh. 4.8 - Prob. 42ECh. 4.8 - Prob. 43ECh. 4.8 - Prob. 44ECh. 4.8 - Prob. 45ECh. 4.8 - Prob. 46ECh. 4.8 - Prob. 47ECh. 4.8 - Prob. 48ECh. 4.8 - Prob. 49ECh. 4.8 - Prob. 50ECh. 4.8 - Prob. 51ECh. 4.8 - Prob. 52ECh. 4.8 - Prob. 53ECh. 4.8 - Prob. 54ECh. 4.8 - Prob. 55ECh. 4.8 - Prob. 56ECh. 4.8 - Prob. 57ECh. 4.8 - Prob. 58ECh. 4 - Prob. 1RCCCh. 4 - Prob. 2RCCCh. 4 - Prob. 3RCCCh. 4 - Prob. 4RCCCh. 4 - Prob. 5RCCCh. 4 - Prob. 6RCCCh. 4 - Prob. 7RCCCh. 4 - Prob. 8RCCCh. 4 - Prob. 9RCCCh. 4 - Prob. 10RCCCh. 4 - Prob. 1RQCh. 4 - Prob. 2RQCh. 4 - Prob. 3RQCh. 4 - Prob. 4RQCh. 4 - Prob. 5RQCh. 4 - Prob. 6RQCh. 4 - Prob. 7RQCh. 4 - Prob. 8RQCh. 4 - Prob. 9RQCh. 4 - Prob. 10RQCh. 4 - Prob. 11RQCh. 4 - Prob. 12RQCh. 4 - Prob. 13RQCh. 4 - If f and g are positive increasing functions on an...Ch. 4 - Prob. 15RQCh. 4 - Prob. 16RQCh. 4 - Prob. 17RQCh. 4 - Prob. 18RQCh. 4 - If f(x) exists and is nonzero for all x, then f(1)...Ch. 4 - limx0xex=1Ch. 4 - Prob. 1RECh. 4 - Prob. 2RECh. 4 - Prob. 3RECh. 4 - Prob. 4RECh. 4 - Prob. 5RECh. 4 - Prob. 6RECh. 4 - Prob. 7RECh. 4 - Prob. 8RECh. 4 - Prob. 9RECh. 4 - Prob. 10RECh. 4 - Prob. 11RECh. 4 - Prob. 12RECh. 4 - Prob. 13RECh. 4 - Prob. 14RECh. 4 - Prob. 15RECh. 4 - Prob. 16RECh. 4 - Prob. 17RECh. 4 - Prob. 18RECh. 4 - Prob. 19RECh. 4 - Prob. 20RECh. 4 - Prob. 21RECh. 4 - Prob. 22RECh. 4 - Prob. 23RECh. 4 - Prob. 24RECh. 4 - Prob. 25RECh. 4 - Prob. 26RECh. 4 - Prob. 27RECh. 4 - Prob. 28RECh. 4 - Prob. 29RECh. 4 - Prob. 30RECh. 4 - Prob. 31RECh. 4 - Prob. 32RECh. 4 - Prob. 33RECh. 4 - Prob. 34RECh. 4 - Prob. 35RECh. 4 - Prob. 36RECh. 4 - Prob. 37RECh. 4 - Prob. 38RECh. 4 - Prob. 39RECh. 4 - Prob. 40RECh. 4 - Prob. 41RECh. 4 - Prob. 42RECh. 4 - Prob. 43RECh. 4 - Prob. 44RECh. 4 - Prob. 45RECh. 4 - Prob. 46RECh. 4 - Prob. 47RECh. 4 - Prob. 48RECh. 4 - Prob. 49RECh. 4 - Prob. 50RECh. 4 - Prob. 51RECh. 4 - Prob. 52RECh. 4 - Prob. 53RECh. 4 - Prob. 54RECh. 4 - Prob. 55RECh. 4 - Prob. 56RECh. 4 - Prob. 57RECh. 4 - Prob. 58RECh. 4 - Prob. 59RECh. 4 - Prob. 60RECh. 4 - Prob. 61RECh. 4 - Prob. 62RECh. 4 - Prob. 63RECh. 4 - Prob. 64RECh. 4 - Prob. 65RECh. 4 - If a rectangle has its base on the x-axis and two...Ch. 4 - Show that sinxcosx2 for all x.Ch. 4 - Prob. 3PCh. 4 - Prob. 4PCh. 4 - Prob. 5PCh. 4 - Find the point on the parabola y = 1 x2 at which...Ch. 4 - Prob. 7PCh. 4 - Prob. 8PCh. 4 - Prob. 9PCh. 4 - Prob. 10PCh. 4 - Prob. 11PCh. 4 - Prob. 12PCh. 4 - Prob. 13PCh. 4 - Prob. 14PCh. 4 - Prob. 15PCh. 4 - Prob. 16PCh. 4 - Prob. 17PCh. 4 - Prob. 18PCh. 4 - Prob. 19PCh. 4 - Prob. 20PCh. 4 - Prob. 21PCh. 4 - Prob. 22PCh. 4 - Prob. 23PCh. 4 - Prob. 24P
Knowledge Booster
Learn more about
Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, calculus and related others by exploring similar questions and additional content below.Recommended textbooks for you
 Calculus: Early TranscendentalsCalculusISBN:9781285741550Author:James StewartPublisher:Cengage Learning
Calculus: Early TranscendentalsCalculusISBN:9781285741550Author:James StewartPublisher:Cengage Learning Thomas' Calculus (14th Edition)CalculusISBN:9780134438986Author:Joel R. Hass, Christopher E. Heil, Maurice D. WeirPublisher:PEARSON
Thomas' Calculus (14th Edition)CalculusISBN:9780134438986Author:Joel R. Hass, Christopher E. Heil, Maurice D. WeirPublisher:PEARSON Calculus: Early Transcendentals (3rd Edition)CalculusISBN:9780134763644Author:William L. Briggs, Lyle Cochran, Bernard Gillett, Eric SchulzPublisher:PEARSON
Calculus: Early Transcendentals (3rd Edition)CalculusISBN:9780134763644Author:William L. Briggs, Lyle Cochran, Bernard Gillett, Eric SchulzPublisher:PEARSON Calculus: Early TranscendentalsCalculusISBN:9781319050740Author:Jon Rogawski, Colin Adams, Robert FranzosaPublisher:W. H. Freeman
Calculus: Early TranscendentalsCalculusISBN:9781319050740Author:Jon Rogawski, Colin Adams, Robert FranzosaPublisher:W. H. Freeman
 Calculus: Early Transcendental FunctionsCalculusISBN:9781337552516Author:Ron Larson, Bruce H. EdwardsPublisher:Cengage Learning
Calculus: Early Transcendental FunctionsCalculusISBN:9781337552516Author:Ron Larson, Bruce H. EdwardsPublisher:Cengage Learning

Calculus: Early Transcendentals
Calculus
ISBN:9781285741550
Author:James Stewart
Publisher:Cengage Learning

Thomas' Calculus (14th Edition)
Calculus
ISBN:9780134438986
Author:Joel R. Hass, Christopher E. Heil, Maurice D. Weir
Publisher:PEARSON

Calculus: Early Transcendentals (3rd Edition)
Calculus
ISBN:9780134763644
Author:William L. Briggs, Lyle Cochran, Bernard Gillett, Eric Schulz
Publisher:PEARSON

Calculus: Early Transcendentals
Calculus
ISBN:9781319050740
Author:Jon Rogawski, Colin Adams, Robert Franzosa
Publisher:W. H. Freeman


Calculus: Early Transcendental Functions
Calculus
ISBN:9781337552516
Author:Ron Larson, Bruce H. Edwards
Publisher:Cengage Learning
Limits and Continuity; Author: The Organic Chemistry Tutor;https://www.youtube.com/watch?v=9brk313DjV8;License: Standard YouTube License, CC-BY