
Concept explainers
a.
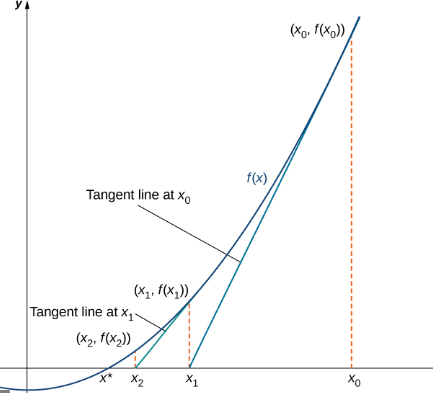
The Newton’s method of obtaining the second approximation by using a graph.
a.
Explanation of Solution
Given information:
The initial approximation is
Calculations:
Newton’s method of obtaining the second approximation is done by using the formula,
For getting the third root the same formula is followed. The process is kept on repeating and it finally converges to a desired root.
b.
The expression for
b.
Explanation of Solution
Given information:
The initial approximation is
Calculations:
Newton’s method of obtaining the second approximation is done by using the formula,
For getting the third root the same formula is followed. The process is kept on repeating and it finally converges to a desired root.
c.
The expression for
c.
Explanation of Solution
Given information:
The initial approximation is
Calculations:
Newton’s method of obtaining the second approximation is done by using the formula,
For getting the third root the same formula is followed. The process is kept on repeating and it finally converges to a desired root.
d.
The circumstances in which Newton’s method is likely to fail or work very ssslow.
d.
Explanation of Solution
Given information:
The initial approximation is
Calculations:
Newton’s method of obtaining the approximation is done by using the formula,
Several approximations are taken and the process is kept on repeating until it finally converges to a desired root. Under certain circumstances the method fails or works very slowly. This happens when
Chapter 4 Solutions
Single Variable Calculus: Concepts and Contexts, Enhanced Edition
 Calculus: Early TranscendentalsCalculusISBN:9781285741550Author:James StewartPublisher:Cengage Learning
Calculus: Early TranscendentalsCalculusISBN:9781285741550Author:James StewartPublisher:Cengage Learning Thomas' Calculus (14th Edition)CalculusISBN:9780134438986Author:Joel R. Hass, Christopher E. Heil, Maurice D. WeirPublisher:PEARSON
Thomas' Calculus (14th Edition)CalculusISBN:9780134438986Author:Joel R. Hass, Christopher E. Heil, Maurice D. WeirPublisher:PEARSON Calculus: Early Transcendentals (3rd Edition)CalculusISBN:9780134763644Author:William L. Briggs, Lyle Cochran, Bernard Gillett, Eric SchulzPublisher:PEARSON
Calculus: Early Transcendentals (3rd Edition)CalculusISBN:9780134763644Author:William L. Briggs, Lyle Cochran, Bernard Gillett, Eric SchulzPublisher:PEARSON Calculus: Early TranscendentalsCalculusISBN:9781319050740Author:Jon Rogawski, Colin Adams, Robert FranzosaPublisher:W. H. Freeman
Calculus: Early TranscendentalsCalculusISBN:9781319050740Author:Jon Rogawski, Colin Adams, Robert FranzosaPublisher:W. H. Freeman
 Calculus: Early Transcendental FunctionsCalculusISBN:9781337552516Author:Ron Larson, Bruce H. EdwardsPublisher:Cengage Learning
Calculus: Early Transcendental FunctionsCalculusISBN:9781337552516Author:Ron Larson, Bruce H. EdwardsPublisher:Cengage Learning





