
The color change accompanying the reaction of phenolphthalein with strong base is illustrated below. The change in concentration of the dye can be followed by spectrophotometry (Section 4.9), and some data collected by that approach are given below. The initial concentrations were [phenolphthalein] = 0.0050 mol/L and [OH‒] = 0.61 mol/L. (Data are taken from review materials for kinetics at chemed.chem.purdue.edu.) (For more details on this reaction see L Nicholson, Journal of Chemical Education, Vol. 66, p. 725, 1989.)

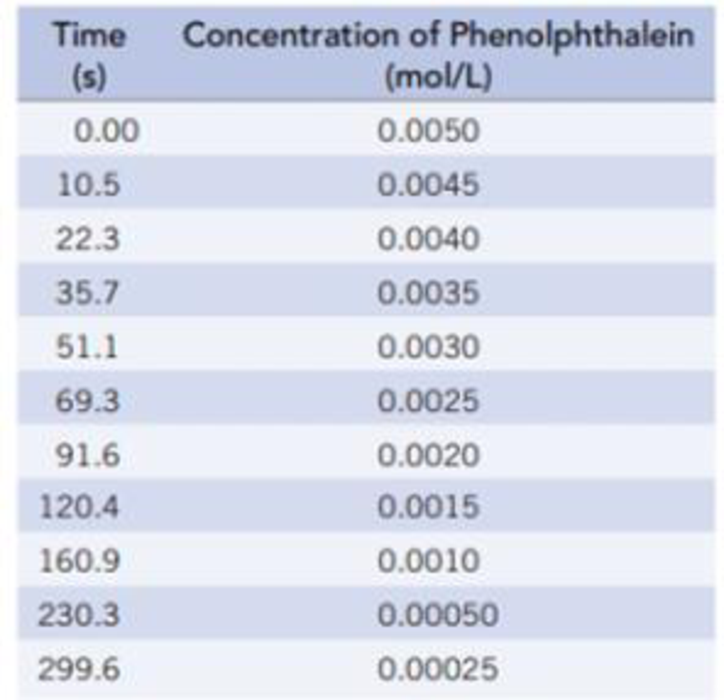
(a) Plot the data above as [phenolphthalein] versus time, and determine the average rate from t = 0 to t = 15 seconds and from t = 100 seconds to t = 125 seconds. Does the rate change? If so, why?
(b) Use a graphical method to determine the order of the reaction with respect to phenolphthalein. Write the rate law, and determine the rate constant.
(c) What is the half-life for the reaction?
Trending nowThis is a popular solution!

Chapter 14 Solutions
Chemistry & Chemical Reactivity
- The label on a bottle of 3% (by volume) hydrogen peroxide, H2O2, purchased at a grocery store, states that the solution should be stored in a cool, dark place. H2O2decomposes slowly over time, and the rate of decomposition increases with an increase in temperature and in the presence of light. However, the rate of decomposition increases dramatically if a small amount of powdered MnO- is added to the solution. The decomposition products are H2O and O2. MnO2 is not consumed in the reaction. Write the equation for the decomposition of H2O2. What role does MnO2 play? In the chemistry lab, a student substituted a chunk of MnO2 for the powdered compound. The reaction rate was not appreciably increased. WTiat is one possible explanation for this observation? Is MnO2 part of the stoichiometry of the decomposition of H2O2?arrow_forward11.41 For a drug to be effective in treating an illness, its levels in the bloodstream must be maintained for a period of time. One way to measure the level of a drug in the body is to measure its rate of appearance in the urine. The rate of excretion of penicillin is first order, with a half-life of about 30 min. If a person receives an injection of 25 mg of penicillin at t = 0, how much penicillin remains in the body after 3 hours?arrow_forwardMost reactions occur by a series of steps. The energy profile for a certain reaction that proceeds by a two-step mechanism is On the energy profile, indicate a. the positions of reactants and products. b. the activation energy for the overall reaction. c. E for the reaction. d. Which point on the plot represents the energy of the intermediate in the two-step reaction? e. Which step in the mechanism for this reaction is rate determining, the first or the second step? Explain.arrow_forward
- The frequency factor A is 6.31 108 L mol1 s1 and the activation energy is 10. kJ/mol for the gas-phase reaction NO(g)+O3(g)NO2(g)+O2(g) which is important in the chemistry of stratospheric ozone depletion. (a) Calculate the rate constant for this reaction at 370. K. (b) Assuming that this is an elementary reaction, calculate the rate of the reaction at 370. K if [NO] = 0.0010 M and [O3] = 0.00050 M.arrow_forwardNitrosyl chloride (NOCI) decomposes to nitrogen oxide and chlorine gases. (a) Write a balanced equation using smallest whole-number coefficients for the decomposition. (b) Write an expression for the reaction rate in terms of [NOCl]. (c) The concentration of NOCl drops from 0.580 M to 0.238 M in 8.00 min. Calculate the average rate of reaction over this time interval.arrow_forwardIodomethane (CH3I) is a commonly used reagent in organic chemistry. When used properly, this reagent allows chemists to introduce methyl groups in many different useful applications. The chemical does pose a risk as a carcinogen, possibly owing to iodomethanes ability to react with portions of the DNA strand (if they were to come in contact). Consider the following hypothetical initial rates data: [DNA]0 ( mol/L) [CH3I]0 ( mol/L) Initial Rate (mol/Ls) 0.100 0.100 3.20 104 0.100 0.200 6.40 104 0.200 0.200 1.28 103 Which of the following could be a possible mechanism to explain the initial rate data? MechanismIDNA+CH3IDNACH3++IMechanismIICH3ICH3++ISlowDNA+CH3+DNACH3+Fastarrow_forward
- Methyl acetate, CH3COOCH3, reacts in basic solution to give acetate ion, CH3COO, and methanol, CH3OH. CH3COOCH3(aq)+OH(aq)CH3COO(aq)+CH3OH(aq) The overall order of the reaction was determined by starting with methyl acetate and hydroxide ion at the same concentrations, so [CH3COOCH3] = [OH] = x. Then Rate=k[CH3COOCH3]m[OH]n=kxm+n Determine the overall order and the value of the rate constant by plotting the following data assuming first- and then second-order kinetics. Time (min) [CH3COOCH3] (mol/L) 0.00 0.01000 3.00 0.00740 4.00 0.00683 5.00 0.00634 10.00 0.00463 20.00 0.00304 30.00 0.00224arrow_forwardFor the reaction of nitrogen monoxide, NO, with chlorine, Cl2, 2NO(g)+Cl2(g)2NOCl(g) the observed rate law is Rate=k[NO]2[Cl2] What is the reaction order with respect to nitrogen monoxide and with respect to Cl2? What is the overall order?arrow_forwardA study of the rate of the reaction represented as 2AB gave the following data: Time (s) 0.0 5.0 10.0 15.0 20.0 25.0 35.0 [A](M) 1.00 0.775 0.625 0.465 0.350 0.205 0.230 (a) Determine the average rate of disappearance of A between 0.0 s and 10.0 s, and between 10.0 s and 20.0 s. (b) Estimate the instantaneous rate of disappearance of A at 15.0 s from a graph of time versus [A]. What are theunits of this rate? (c) Use the rates found in parts (a) and (b) to determine the average rate of formation of B between 0.00 s and 10.0 s, and the instantaneous rate of formation of B at 15.0 s.arrow_forward
- 11.93 On a particular day, the ozone level in Milwaukee exceeded the EPAs 1-hour standard of 0.12 ppin by 10 ppb. How many ozone molecules would be present in 1 liter of air at the detection site?arrow_forwardThe isomerization of cyclopropane, C3H6, is believed to occur by the mechanism shown in the following equations: C3H6+C3H5k1C3H6+C3H6(Step1)C3H6k2C2=CHCH3(Step2) Here C3H6 is an excited cyclopropane molecule. At low pressure, Step 1 is much slower than Step 2. Derive the rate law for this mechanism at low pressure. Explain.arrow_forwardOne experimental procedure that can be used to determine the rate law of a reaction is the method of initial rates. What data are gathered in the method of initial rates, and how are these data manipulated to determine k and the orders of the species in the rate law? Are the units for k. the rate constant, the same for all rate laws? Explain. If a reaction is first order in A, what happens to the rate if [A] is tripled? If the initial rate for a reaction increases by a factor of 16 when [A] is quadrupled, what is the order of n? If a reaction is third order in A and [A] is doubled, what happens to the initial rate? If a reaction is zero order, what effect does [A] have on the initial rate of a reaction?arrow_forward
 Chemistry: The Molecular ScienceChemistryISBN:9781285199047Author:John W. Moore, Conrad L. StanitskiPublisher:Cengage Learning
Chemistry: The Molecular ScienceChemistryISBN:9781285199047Author:John W. Moore, Conrad L. StanitskiPublisher:Cengage Learning
 Chemistry: Principles and PracticeChemistryISBN:9780534420123Author:Daniel L. Reger, Scott R. Goode, David W. Ball, Edward MercerPublisher:Cengage Learning
Chemistry: Principles and PracticeChemistryISBN:9780534420123Author:Daniel L. Reger, Scott R. Goode, David W. Ball, Edward MercerPublisher:Cengage Learning Chemistry: An Atoms First ApproachChemistryISBN:9781305079243Author:Steven S. Zumdahl, Susan A. ZumdahlPublisher:Cengage Learning
Chemistry: An Atoms First ApproachChemistryISBN:9781305079243Author:Steven S. Zumdahl, Susan A. ZumdahlPublisher:Cengage Learning ChemistryChemistryISBN:9781305957404Author:Steven S. Zumdahl, Susan A. Zumdahl, Donald J. DeCostePublisher:Cengage Learning
ChemistryChemistryISBN:9781305957404Author:Steven S. Zumdahl, Susan A. Zumdahl, Donald J. DeCostePublisher:Cengage Learning Chemistry for Engineering StudentsChemistryISBN:9781337398909Author:Lawrence S. Brown, Tom HolmePublisher:Cengage Learning
Chemistry for Engineering StudentsChemistryISBN:9781337398909Author:Lawrence S. Brown, Tom HolmePublisher:Cengage Learning





