
Concept explainers
Three identical halls are thrown from the top of a building, all with the same initial speed. The first ball is thrown horizontally, the second at some angle above the horizontal, and the third at some angle below the horizontal, as in Figure 5.16. Neglecting air resistance, rank the speeds of the balls as they reach the ground, from fastest to slowest. (a) 1, 2, 3 (b) 2, 1, 3 (c) 3, 1, 2 (d) All three balls strike the ground at the same speed.
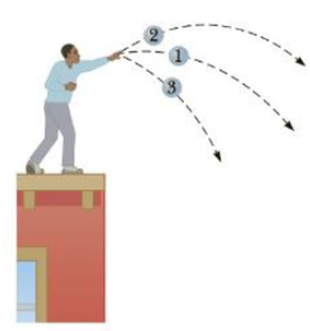
Figure 5.16 (Quick Quiz 5.3) A student throws three identical balls from the top of a building, each at the same initial speed hut at a different initial angle.
Trending nowThis is a popular solution!

Chapter 5 Solutions
College Physics
Additional Science Textbook Solutions
Applied Physics (11th Edition)
Matter and Interactions
Physics for Scientists and Engineers with Modern Physics
Fundamentals Of Physics - Volume 1 Only
- A space shuttle with a mass of 189 kg is fired upwards from the earth's surface, at the equator, at a speed of 9.94 · 103 m/s. If there was no air resistance, how high would the shuttle reach if it went straight up?arrow_forwardA stone thrown from the top of a 50-meter tall building at a speed of 16 m/s and at an angle of 30 degrees below the horizontal. What will be its speed (in m/s) two seconds later?arrow_forwardIn the very Dutch sport of ducth-dude-on-a-pole, athletes run up to a long pole and then use it to vault across a canal. At the very top of his arc, a 70kg vaulter is moving at 3.5m/s and is 5.0m from the bottom end of the pole. What vertical force does the pole exert on the vaulter (in magnitude)?arrow_forward
- A particle is projected vertically upward in a constant gravitational field with an initial speed 0. Show that if there is a retarding force proportional to the square of the instantaneous speed, the speed of the particle when it returns to the initial position is 0t02+t2 where t, is the terminal speed.arrow_forwardA small object begins a free fall from a height of 29.0 m. After 1.10 s, a second small object is launched vertically upward from the ground with an initial velocity if 37.0 m/s. At what height h above the ground will the two objects first meet? Asked to use the equation y=y0+v0yt--1/2gt^2 and assume gravity as I believe 9.8 m/s^2arrow_forwardA roadrunner is cruising at 6 m/s without knowing the road under its feet is about to run out, at the edge of a cliff, some 25 m above a flat valley below. Fortunately a roadrunner CAN fly so it just flew away. If indeed the roadrunner couldn't fly and would not be affected by air drag, how long will it take to hit the valley (flat) below?arrow_forward
- You are standing at the top of a cliff that has a stairstep configuration. There is a vertical drop of 6 m at your feet, then a horizontal shelf of 5 m , then another drop of 4 m to the bottom of the canyon, which has a horizontal floor. You kick a 0.44 kg rock, giving it an initial horizontal velocity that barely clears the shelf below What initial horizontal velocity v will be required to barely clear the edge of the shelf below you? The acceleration of gravity is 9.8 m/s^2 . Consider air friction to be negligible. Answer in units of m/s. How far from the bottom of the second cliff will the projectile land? Answer in units of m.arrow_forwardSuppose that you loft the ball with an initial speed of v = 16.1 m/s, at an angle of θ = 51.8° above the horizontal. At this instant your opponent is d = 10.7 m away from the ball. He begins moving away from you 0.300 s later, hoping to reach the ball and hit it back at the moment that it is h = 2.02 m above its launch point. With what minimum average speed must he move? (Ignore the fact that he can stretch, so that his racket can reach the ball before he does.)arrow_forwardConsider a circular-motion problem in which tension not only must provide the proper radial acceleration but also must balance gravity. As we shall see, it can do both. A tetherball is attached to a swivel in the ceiling by a light cord of length L, as measured from the ceiling to the center of the tetherball. When the ball is hit by a paddle, it swings in a horizontal circle with constant speed vv, and the cord makes a constant angle β with the vertical direction. The ball goes through one revolution in time T. Assuming that T, mass mm, and length L of the rope are known, derive algebraic expressions for the tension FT in the cord and the angle β. a)What is the period T of the ball’s motion if L=2.0m and the cord makes an angle of β=40∘with the vertical?arrow_forward
- A ball of mass 0.3 kg, initially at rest, is kicked directly toward a fence from a point 20 m away, as shown below. The velocity of the ball as it leaves the kicker’s foot is 17 m/s at angle of 47 ◦ above the horizontal. The top of the fence is 6 m high. The ball hits nothing while in flight and air resistance is negligible. The acceleration due to gravity is 9.8 m/s2 (meters/seconds/squared). 1) How far above the top of fence will the ball pass? Consider the diameter of the ball to be negligible. Answer in units of m. 2) What is the vertical component of the velocity when the ball reaches the plane of the fence? Answer in units of m/s.arrow_forwardA cannon fires a 0.292 kg shell with initial velocity vi = 8.2 m/s in the direction θ = 45 ◦ above the horizontal. The shell’s trajectory curves downward because of gravity, so at the time t = 0.643 s the shell is below the straight line by some vertical distance ∆h. Find this distance ∆h in the absence of air resistance. The acceleration of gravity is 9.8 m/s 2 . Answer in units of m.arrow_forwardA rifle is aimed horizontally toward the center of a target 30 m away. If the bullet strikes 1.9 cm below the center, what was the velocity of the bullet? Ignore air friction. the bullet? Ignore air friction.)arrow_forward
 Principles of Physics: A Calculus-Based TextPhysicsISBN:9781133104261Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning
Principles of Physics: A Calculus-Based TextPhysicsISBN:9781133104261Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning Classical Dynamics of Particles and SystemsPhysicsISBN:9780534408961Author:Stephen T. Thornton, Jerry B. MarionPublisher:Cengage Learning
Classical Dynamics of Particles and SystemsPhysicsISBN:9780534408961Author:Stephen T. Thornton, Jerry B. MarionPublisher:Cengage Learning

