
Let P(x1, y1) be a point on the parabola y2 = 4px with focus F(p, 0). Let α be the angle between the parabola and the line segment FP, and let β be the angle between the horizontal line y = y1, and the parabola as in the figure. Prove that α = β. (Thus. by a principle of geometrical optics. light from a source placed at F will be reflected along a line parallel to the x-axis. This explains why paraboloids, the surfaces obtained by rotating parabolas about their axes, are used as the shape of some automobile headlights and mirrors for telescopes.)
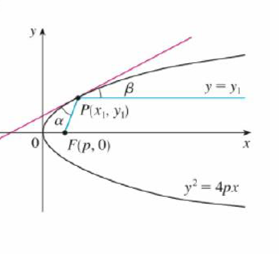
To show: The angle between the parabola and the line segment FP is equal to the angle between the parabola and the line
Explanation of Solution
Proof:
The equation of the parabola is,
Let
Let
Obtain the slope of the tangent line at
Differentiate
Thus, the slope of the tangent at
The slope of the line passing through
The angle between the tangent line at P and the line
Substitute
Since
Since the tangent line at
In
Hence the required result is proved.
Chapter 3 Solutions
Single Variable Calculus: Concepts and Contexts, Enhanced Edition
Additional Math Textbook Solutions
University Calculus
Thomas' Calculus: Early Transcendentals (14th Edition)
Calculus Early Transcendentals, Binder Ready Version
Single Variable Calculus: Early Transcendentals (2nd Edition) - Standalone book
Calculus & Its Applications (14th Edition)
Calculus and Its Applications (11th Edition)
 Calculus: Early TranscendentalsCalculusISBN:9781285741550Author:James StewartPublisher:Cengage Learning
Calculus: Early TranscendentalsCalculusISBN:9781285741550Author:James StewartPublisher:Cengage Learning Thomas' Calculus (14th Edition)CalculusISBN:9780134438986Author:Joel R. Hass, Christopher E. Heil, Maurice D. WeirPublisher:PEARSON
Thomas' Calculus (14th Edition)CalculusISBN:9780134438986Author:Joel R. Hass, Christopher E. Heil, Maurice D. WeirPublisher:PEARSON Calculus: Early Transcendentals (3rd Edition)CalculusISBN:9780134763644Author:William L. Briggs, Lyle Cochran, Bernard Gillett, Eric SchulzPublisher:PEARSON
Calculus: Early Transcendentals (3rd Edition)CalculusISBN:9780134763644Author:William L. Briggs, Lyle Cochran, Bernard Gillett, Eric SchulzPublisher:PEARSON Calculus: Early TranscendentalsCalculusISBN:9781319050740Author:Jon Rogawski, Colin Adams, Robert FranzosaPublisher:W. H. Freeman
Calculus: Early TranscendentalsCalculusISBN:9781319050740Author:Jon Rogawski, Colin Adams, Robert FranzosaPublisher:W. H. Freeman
 Calculus: Early Transcendental FunctionsCalculusISBN:9781337552516Author:Ron Larson, Bruce H. EdwardsPublisher:Cengage Learning
Calculus: Early Transcendental FunctionsCalculusISBN:9781337552516Author:Ron Larson, Bruce H. EdwardsPublisher:Cengage Learning





